
Yesterday, I studied the algorithm of the Hanno Tower for a day. I felt that my IQ was crushed. It was not as good as the orangutan in "The Rise of the Gorilla Ball"! ! !
It is said that the person who first invented this problem was the French mathematician "Edward Lucas".
In the holy temple of Benares (in northern India) in the center of the world, there are three gem needles inserted on a brass plate. When Brahma, the main god of Hinduism, created the world, he threaded 64 gold pieces from large to small on one of the needles from bottom to top. This is the so-called Tower of Hanoi. No matter day or night, there is always a monk moving these gold pieces according to the following rules: only move one piece at a time, no matter which needle it is on, the small piece must be on top of the large piece. The monks predicted that when all the gold pieces are moved from the needle threaded by Brahma to another needle, the world will be wiped out with a thunderbolt, and the Vatican Tower, temples and all living beings will also perish together.
There are many variations of this legend and it is unknown who it is, but the mathematical problems left behind are very classic.
The mathematical knowledge he left behind: the relationship between the number of gold pieces and the number of moving steps is 2^n - 1.
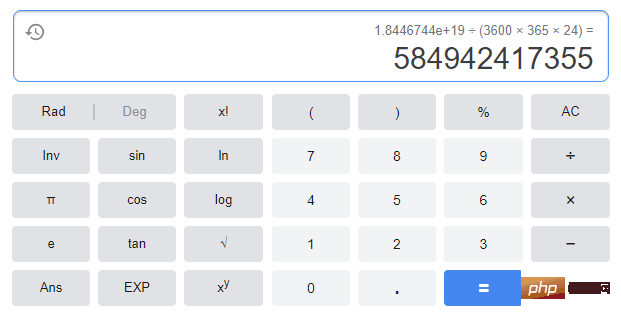
If the legend True, the monks needed 2^64 - 1 steps to complete this task; assuming they moved one gold piece per second, it would take 584.9 billion years to complete. The entire universe is only 13.7 billion years old, so it is still early for the destruction of the universe... (I was bored, so I did the calculation, as shown below)
Basic rules
The Tower of Hanoi algorithm has two basic conditions, assuming that the moving plate is a plate.
1. Only one plate can be moved at a time.
2. The small plate must be on top of the large plate.
Suppose there are 3 pillars in this game, namely A, B, and C. There are already N sorted plates on one of them, the largest one is at the bottom, and the plates are getting smaller and smaller going up, and there are two other empty columns.
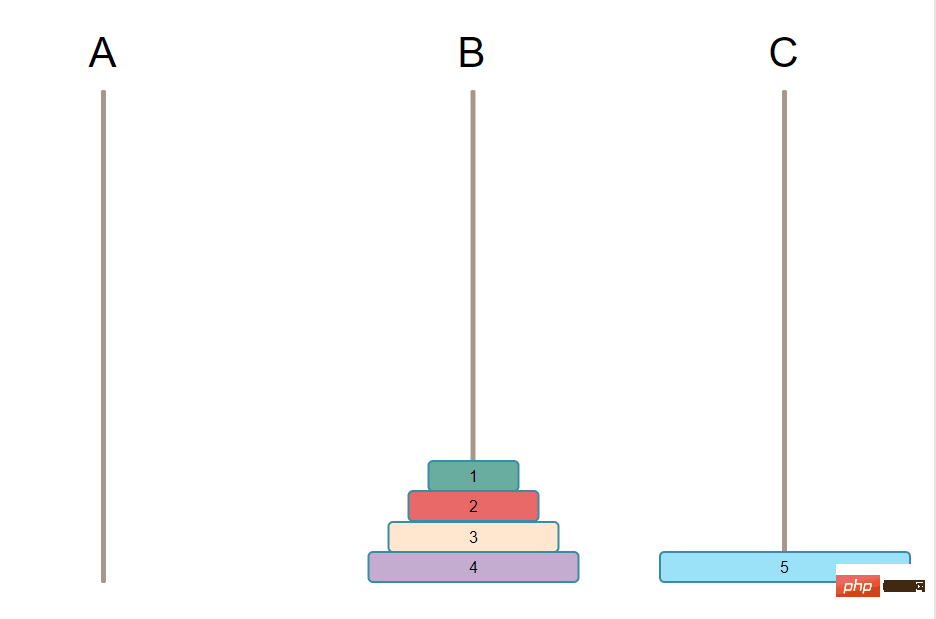
The initial state is as shown below:
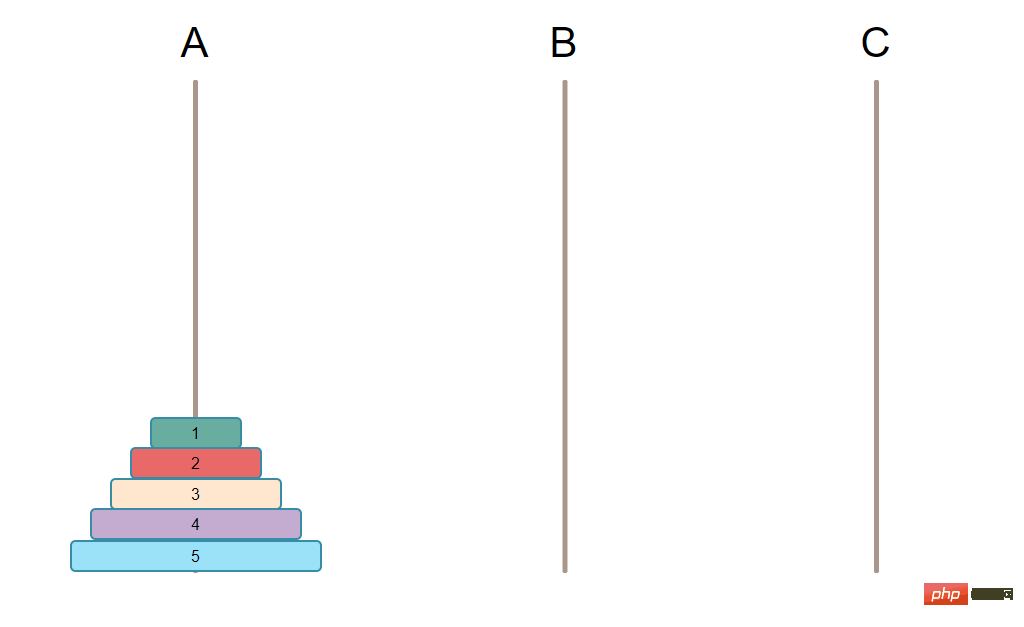
The ultimate goal that needs to be achieved is to move all the plates on the pillar to another pillar. [Recommended learning: PHP video tutorial]
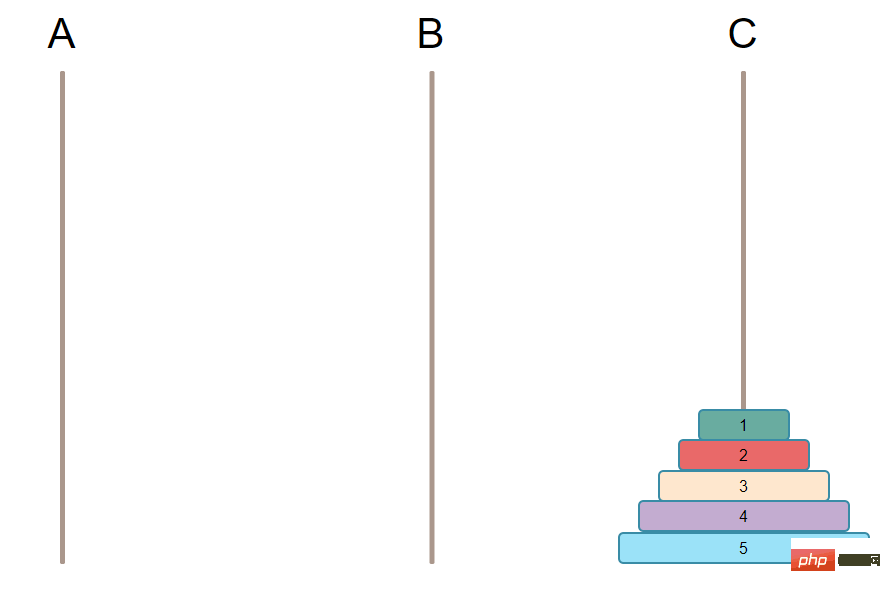
General idea of implementation:
N-1 plates to pillar B. Only in this way can the Nth plate (that is, the largest plate) can be moved to pillar C. N-1 plates to pillar B. Because the big ones must be at the bottom and the small ones at the top to meet the conditions, these N-1 plates It is also sequential on the B pillar. To summarize:
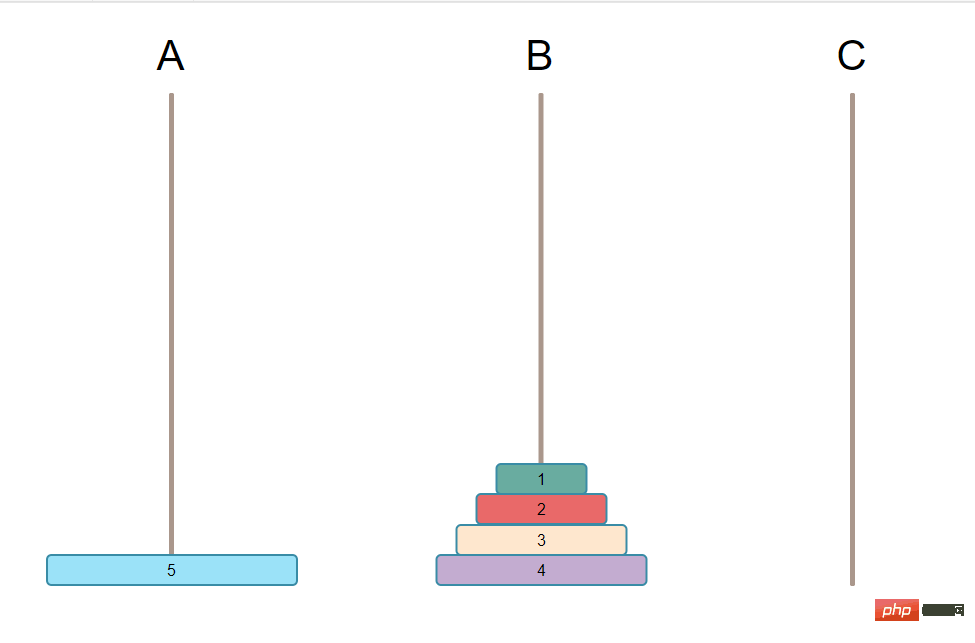
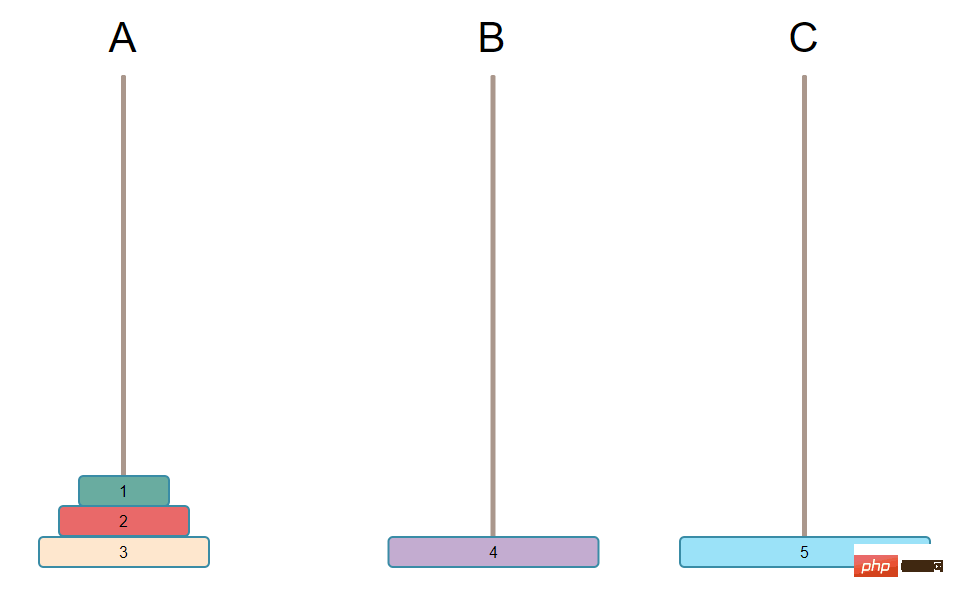
The first step is to move N-1 plates on A to B.
Why do we need to move N-1 to B first? You see, because what you ultimately achieve is to move all the plates on A to C, the order cannot be changed, it can only be that the big ones are at the bottom and the small ones are at the top. Then you definitely need to move the largest one to C first, otherwise the conditions will not be met.
To move the largest plate from A to C, the largest plate on A must be vacated, that is, all the plates on the largest plate must be moved. And you only have 3 pillars. There must be no other plate handles on C, otherwise you will not meet the conditions again. All these N-1 plates can only be placed on B, and they are still in order. It becomes the following picture:
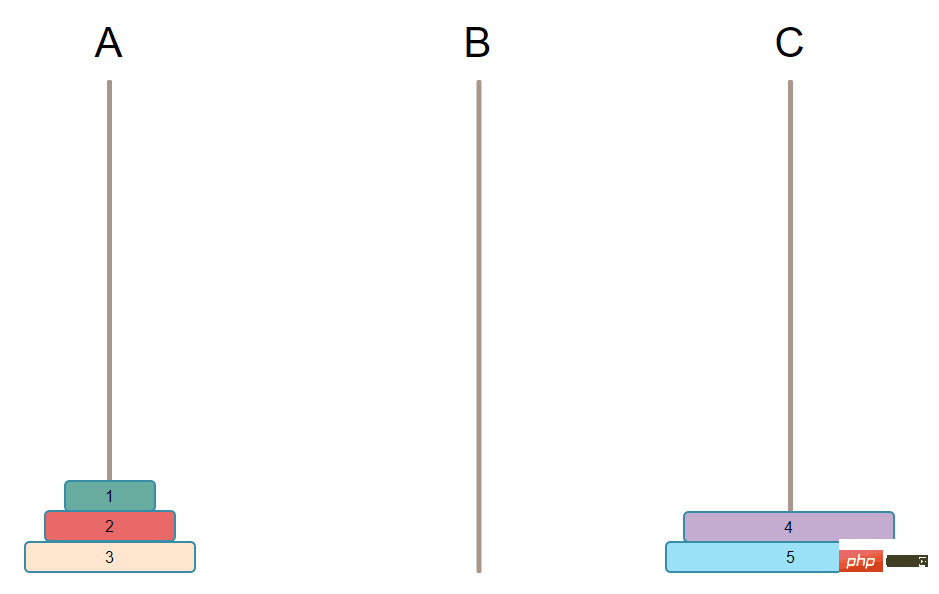
The second step is to move the Nth plate on A (that is, the largest plate) to C.
This is very simple. Just move the largest plate from A to C in one step. As shown below:
The third step is to move N-1 plates on B to C.
Note: To move N-1 plates to C, does it turn into finding the largest plate among them, and then moving the largest plate first. So here it actually becomes a matter of repeating steps 1 and 2, finding the largest one among these N-1 and moving it to C first, and the cycle repeats.
The third step is actually equivalent to changing the requirements. Assume K = N - 1.
There are K plates on pillar B, pillar A is empty, and pillar C has the largest plate, so for pillar B with K plates, it is equivalent to being empty.
The first step is to move K-1 plates on B to A.
The second step is to move the Kth plate on B to C.
The third step is to move K-1 plates on A to C.
…
It becomes the picture below
First find the largest one among the remaining plates
Then move the largest plate
Then loop until there is only one plate left, move directly to C, and the game is over.
What are auxiliary pillars? Assume that all the plates you want to move are on A, and the goal is to move to C, then B is the auxiliary pillar of N-1 plates. Because they can only exist here temporarily, otherwise they will not meet the rules of the game.
Here we need to find out the auxiliary pillars first. Don’t think about how to implement them, but clarify the logic first.
Through the above analysis, we can see that this is actually a repeated operation in a cycle, which is very Similar to recursion, everything here can be implemented using recursion.
To use recursion, there are two necessary conditions
1. Find the recursion formula
2. Find the exit condition
Exit condition It’s easy to write. It must be moved directly to the C pillar when there is only one plate.
So what is the recursion formula? Based on the above logical analysis, it can be decomposed into 3 steps.
The first step is to move the [N-1] plates from A to B
The second step is to move the [Nth] plate from A to C
The third step is to move the [remaining N-1] plates from B to C
The following is the pseudo code implemented in PHP:
class HanoiTower
{
// 计数器
public $count = 0;
/**
* 汉诺塔实现
*
* @param $n 盘子号
* @param $A 初始柱子
* @param $B 中转站
* @param $C 目标柱子
*/
public function hanoi($n, $A, $B, $C)
{
if ($n == 1) {
// 退出条件 只剩一个盘子的时候直接从A移动到C
$this->biggestOne($n, $A, $B, $C);
} else {
// Analyze how PHP implements the interesting Tower of Hanoi algorithm把 【n-1】 个盘子从A移动到B 此时C为中转站
$this->hanoi($n - 1, $A, $C, $B);
// Analyze how PHP implements the interesting Tower of Hanoi algorithm把 【第n】 个盘子从A移动到C
$this->biggestOne($n, $A, $B, $C);
// 第三步把B上 【剩余的n-1个】 盘子从B移动到C 此时A为中转站
$this->hanoi($n - 1, $B, $A, $C);
}
}
/**
* 移动最大的盘子
* 直接从A移动到C
*/
public function biggestOne($n, $A, $B, $C)
{
++$this->count;
echo '第', $this->count, '步 ', '把 ', $n, '从 ', $A, '移动到', $C, '<br />';
}
}
$n = 5;
$hanoiTower = new HanoiTower();
echo '这是一个有 【', $n, '】 个盘子的汉诺塔:', '<br />';
// 调用执行
$hanoiTower->hanoi($n, 'A', 'B', 'C');
echo '总共需要走:【', $hanoiTower->count, '】 步';Result as follows:

The above is the detailed content of Analyze how PHP implements the interesting Tower of Hanoi algorithm. For more information, please follow other related articles on the PHP Chinese website!