PHP data structure-graph traversal: depth first and breadth first-PHP Tutorial-php.cn

Traversal of graphs: depth first and breadth first

In the previous article "PHP Data Structure-Graph Storage Structure", we have learned the relevant storage structures of graphs. That is, adjacency matrix and adjacency list. They represent the two most typical types of sequential storage and chained storage respectively. Now that we have the data structures, of course our next step is to learn how to operate these data structures, which is the algorithm part. Whether it is a graph or a tree, traversal is a very important part. Today we will first learn the two most basic graph traversal methods.

Tree traversal evolved into graph traversal

Remember that in the study of trees, we talked about pre-order, in-order, post-order and level-order traversal What are these traversal forms? In fact, pre-order, mid-order and post-order can be regarded as a kind of traversal method. They all use the stack structure to traverse. The characteristic is to go to the black path first, and then return to the untraversed path. Level-order traversal uses a queue to traverse layer by layer. Its characteristic is that it first traverses the child nodes, and then traverses the next level nodes of each child node one by one.

After reviewing the tree traversal method, it will be very simple to learn the graph traversal method, because in graph traversal, the most basic two traversal forms are based on stack and queue. It’s just that their names are slightly different. The stack-based traversal method is called depth-first traversal, while the queue-based traversal method is called breadth-first traversal. In fact, it corresponds to the first, middle, and last order traversal and layer order traversal in the tree. There is not much difference in essence.

[Recommended: PHP video tutorial]

Depth-first traversal

We still traverse from the stack Start with the method, which is the form of depth-first traversal in the figure. For the stack, new nodes are continuously pushed onto the stack until it is found that it has no other child nodes, and then the original path is returned. When a node is found to have other nodes, then the child node is pushed onto the stack. This is the idea of deep traversal.

Here, it should be noted that we need to record the nodes that have been visited. When there are multiple nodes with paths connected to a certain node, ensure that this node has only been visited once. . This is the biggest difference from the tree structure, because the tree is all the way down, there is no connection between horizontal nodes, and a node has only one superior node. In a graph, any node can be related to any other node.

Adjacency Matrix

First, let’s look at the implementation of the depth-first traversal algorithm for the adjacency matrix. It doesn’t matter if you don’t understand it now. Scroll down to see the illustrations and then read them together. Of course, a better solution is to run it yourself.

$visited = []; // 已访问结点
function DFS_AM($graphArr, $x)
{
    global $visited;
    echo "节点：{$x}", PHP_EOL;
    $visited[$x] = true; // 当前结点标记为已访问
     
    // y 就是邻接矩阵中的横行
    for ($y = 1; $y <= count($graphArr); $y++) {
        // 循环判断第 [x][y] 个数据是否为 1，也就是是否有边
        // 并且这个结点没有被访问过
        if ($graphArr[$x][$y] != 0 && !$visited[$y]) {
            // 进行栈递归，传递的参数是当前这个结点
            DFS_AM($graphArr, $y);
        }
    }
}
BuildGraph($graphArr); // 建立邻接矩阵图
echo &#39;请输入开始遍历的结点（1-结点数）：&#39;; 
fscanf(STDIN, "%d", $startNode); // 输入从第几个结点开始访问
DFS_AM($graphArr, $startNode); // 开始深度优先遍历

Copy after login

The amount of code is not much. I use the code for establishing the adjacency matrix in the previous article. If you have forgotten it, go back and have a look or directly read the source code from the link at the bottom of the article.

Next we test:

# php 5.3图的遍历：深度优先与广度优先.php
输入结点数：4
请输入边数：3
请输入边，格式为 出 入 权：1 2 1
请输入边，格式为 出 入 权：1 3 1
请输入边，格式为 出 入 权：3 4 1
请输入开始遍历的结点（1-结点数）：3
节点：3
节点：1
节点：2
节点：4

Copy after login

Adjacency list

Of course, the idea of traversing the adjacency list is the same, except that the loop algorithm in the middle is used is the way of chain characteristics.

$visited = [];  // 已访问结点
function DFS_AL($graph, $x){
    global $visited;
    $p = $graph->adjList[$x]; // 指定结点的第一个边结点
    echo "节点：{$x}", PHP_EOL; // 输出指定结点的信息
    $visited[$x] = true; // 设置该结点已被访问
    while($p != null){
        $y = $p->adjVex; // 获得边结点信息
        if(!$visited[$y]){ // 如果结点没有被访问过
            DFS_AL($graph, $y); // 进入这个边结点的深度遍历过程
        }
        $p = $p->nextArc; // 移动到下一个边结点
    }
}
$graph = BuildLinkGraph();
$graphBFS = $graph;
echo &#39;请输入开始遍历的结点（1-结点数）：&#39;;
fscanf(STDIN, "%d", $startNode); // 输入从第几个结点开始访问
DFS_AL($graph, $startNode);// 开始深度优先遍历

Copy after login

Is it also very simple? Let’s simply test it next:

# php 5.3图的遍历：深度优先与广度优先.php
请输入 结点数 边数：
4 3
请输入边，格式为 出 入 权：1 2 1
请输入边，格式为 出 入 权：1 3 1
请输入边，格式为 出 入 权：3 4 1
请输入开始遍历的结点（1-结点数）：3
节点：3
节点：4
节点：1
节点：2

Copy after login

Why is the output order different from that of the adjacency matrix? The adjacency list we implemented in the previous article uses head interpolation. The later input data is added in front of the node link. If we put 3 4 1 in the first input, then the node will be the same as the adjacency matrix. The traversal results are the same.

Depth-First Traversal Illustration

I came up directly to look at the code, and talked about the algorithm for a long time. Are you still confused? It doesn't matter, let's take a look at the picture directly:

PHP data structure-graph traversal: depth first and breadth first

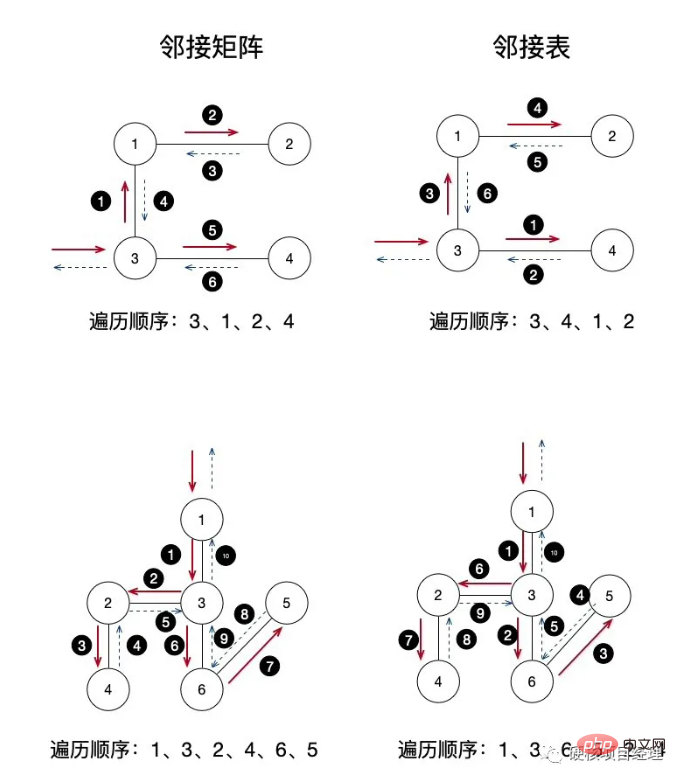
The left side is the adjacency matrix, and the right side is the adjacency list. The graph we tested is relatively simple, with 4 nodes and 3 edges. The following is a more complex graph with 6 nodes and 5 edges. You can test it yourself. For the traversal and execution order of each step, look at the numbers in the small black circles. Let's use the first picture of the adjacency matrix to briefly explain the steps of access:

First we input the access starting from node 3, and then start the depth traversal, and then output the result Point 3
In the first step of the loop, node 3 has an edge with node 1, so node 1 is recursively passed in, and node 1 is pushed onto the stack
Output node 1, node 1 in the current recursion is on the top of the stack
在结点1 的循环中发现结点1 和结点 2 有边，于是递归传入结点2 ，结点2 入栈
输出结点2，目前的递归中结点2 在栈顶
注意了，重点在这里，结点2 的循环中没有发现与其它未访问的结点有边存在了，于是递归开始返回，也就是开始出栈了，依次返回到结点1 、结点3，没有任何输出，栈空了，递归回到最外层的函数了
继续结点3 的循环，发现与结点4 有边，递归传入结点4
输出结点4，目前的递归中结点4 在栈顶
结点4 的循环中没有发现其它未访问的结点及边了，递归返回，结点4 出栈
结点3 循环完成，遍历结束

一步一步的很清晰吧，大家试着自己分析一下下面那个复杂一些图的深度遍历顺序，看看和我们程序输出的结果是不是一样的。在很多的考研或者数据结构考试中，经常会有选择题或应用题让你手动地来写出深度优先遍历的顺序哦！

广度优先遍历

接下来就是广度优先遍历了，其实说白了就是我们在学习树的遍历时候的层序遍历。前面我们说过，深度遍历是一条路走到黑，没路了退回来。而广度遍历则是一层一层的查看，直到找到出口。

邻接矩阵

使用邻接矩阵来进行广度优先遍历的操作，其实最核心的遍历方式和深度遍历没什么区别，都是对某一个结点进行边的查找，唯一不同的就是把递归栈换成了队列而已。

$visited = [];
function BFS_AM($graphArr, $x){
    global $visited;
    $queue = InitSqQueue(); // 初始化队列
    $graphCount = count($graphArr); // 获取矩阵结点数量
    $visited[$x] = true; // 结点标记为已访问
    EnSqQueue($queue, $x); // 结点入队
    while($x){ // 循环判断结点是否 fasle
        // 遍历所有结点是否与这个结点有边
        for ($y = 1; $y <= $graphCount; $y++) {
            // 如果有边并且未访问过
            if ($graphArr[$x][$y] != 0 && !$visited[$y]) {
                $visited[$y] = true; // 结点标记为已访问
                EnSqQueue($queue, $y); // 结点入队
            }
        }
        $x = DeSqQueue($queue); // 出队一个结点
        echo $x, PHP_EOL; // 输出结点
    }
}
echo &#39;请输入开始广度遍历的结点（1-结点数）：&#39;;
fscanf(STDIN, "%d", $startNode);
BFS_AM($graphArr, $startNode); // 开始广度遍历

Copy after login

代码中的注释也很清晰明了了，我们直接进行测试：

……
……
请输入开始广度遍历的结点（1-结点数）：3
3
1
4
2

Copy after login

邻接表

同样地，我们也提供邻接表的链式广度优先遍历的核心函数。

$visited = [];
function BFS_AL($graph, $x){
    global $visited;
    $visited[$x] = true; // 结点标记为已访问
    $queue = InitSqQueue();// 初始化队列
    EnSqQueue($queue, $x); // 结点入队
    
    // 如果一直有能出队的结点，就一直循环
    // 也就是说，如果队列空了，循环就结束
    while(($i = DeSqQueue($queue))!==false){
        echo $i, PHP_EOL; // 输出结点
        $p = $graph->adjList[$i]; // 结点的第一个边结点
        while($p != null){ // 如果不为空
            $y = $p->adjVex; // 边结点信息
            if(!$visited[$y]){ // 如果没有访问过
                $visited[$y] = true; // 标记结点为已访问
                EnSqQueue($queue, $y); // 入队结点
            }
            $p = $p->nextArc; // 结点指针指向下一个
        }
    }
}
echo &#39;请输入开始遍历的结点（1-结点数）：&#39;;
fscanf(STDIN, "%d", $startNode);
BFS_AL($graph, $startNode); // 开始广度遍历

Copy after login

核心的循环中的操作其实也和深度遍历没什么太大的区别，同样是换成了队列这种存储形式而已。

……
……
请输入开始广度遍历的结点（1-结点数）：3
3
4
1
2

Copy after login

广度优先遍历图示

好吧，上面又罗列完了算法，接下来就是图示的时间了，相信还是一看图大家就马上能明白广度优先遍历的具体步骤了。

PHP data structure-graph traversal: depth first and breadth first

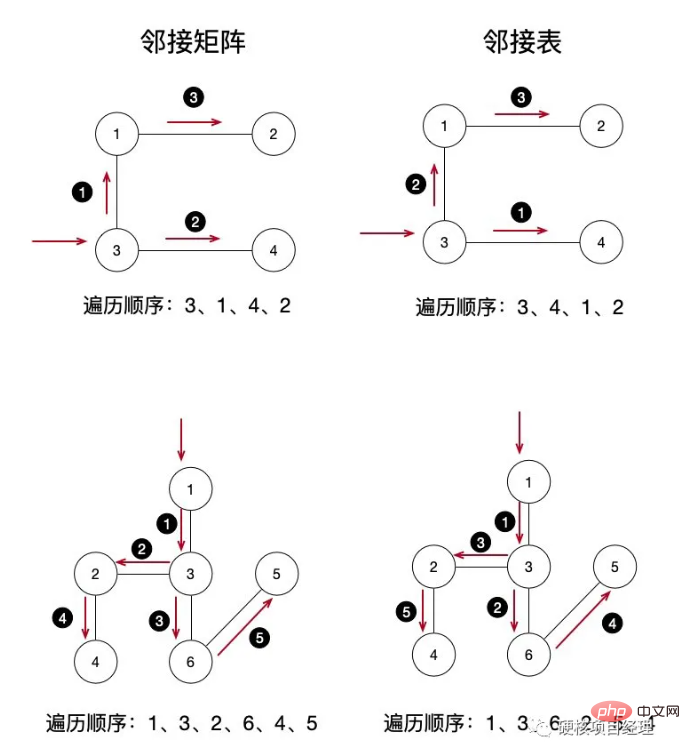
和上面的图一样，同样还是左边是邻接矩阵，右边是邻接表。在这里，我们依然还是直接分步骤来看一下左边最上面图的遍历操作顺序：

输入结点3 开始广度遍历，结点标记为已访问，这时结点3 入队
使用 while 循环判断结点x 是否为 null ，如果不为 null 进入循环体
遍历所有结点是否与这个结点有边，如果有边，并且这个结点没有被访问过，标记已访问，加入队列
出队一个元素，并赋值给 x
输出 x 结点的信息

广度优先遍历没有栈的回溯，就是一条线性的队列走完就完了，所以图示会非常清晰。单独一个结点我们会将和它相关的所有结点入队，然后出队最顶上的结点，这样就能够像树的层序遍历一样按照一层一层的顺序来遍历整个图。同样地，拿起纸笔，找复杂一点的图，试试能不能手写出类似于广度优先遍历顺序的题目吧！

总结

大家学完了之后是不是发现今天介绍的深度优先和广度优先两种遍历方式真的和树的遍历方式没什么太大的区别。最大的不同就是我们要标记已访问过的结点而已。不管怎么说，使用栈和队列来对树或图进行遍历是所有树和图的操作算法中最最基础的部分，也是考试和面试中最常见的问题，大家一定要深入理解掌握哦！

测试代码：
https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/5.图/source/5.3图的遍历：深度优先与广度优先.php

Copy after login

The above is the detailed content of PHP data structure-graph traversal: depth first and breadth first. For more information, please follow other related articles on the PHP Chinese website!