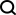SPFA algorithm usage tutorial
Scope of application: There are negative weight edges in a given graph. At this time, algorithms such as Dijkstra have no place to use, and the complexity of the Bellman-Ford algorithm is too high, so the SPFA algorithm comes in handy. . We agree that there is no negative weight cycle in the directed weighted graph G, that is, the shortest path must exist. Of course, we can do a topological sort before executing the algorithm to determine whether there is a negative weight cycle, but this is not the focus of our discussion.
Algorithm idea: We use array d to record the shortest path estimate of each node, and use an adjacency list to store graph G. The method we adopt is the dynamic approximation method: set up a first-in-first-out queue to save the nodes to be optimized. During optimization, we take out the head node u each time, and use the current shortest path estimate of point u to leave point u. The node v pointed to undergoes a relaxation operation. If the shortest path estimate of point v is adjusted and point v is not in the current queue, point v is placed at the end of the queue. In this way, nodes are continuously taken out from the queue to perform relaxation operations until the queue is empty
The expected time complexity is O(ke) , where k is the average number of times all vertices enter the team. It can be proved that k is generally less than or equal to 2.
Implementation method:
Create a queue. Initially, there is only the starting point in the queue. , and then create a table to record the shortest path from the starting point to all points (the initial value of the table should be assigned to the maximum value, and the path from the point to itself should be assigned to 0). Then perform a relaxation operation, using some points in the queue as the starting point to refresh the shortest path to all points. If the refresh is successful and the refreshed point is not in the queue, the point is added to the end of the queue. Repeat until the queue is empty.
Determine whether there is a negative loop:
If a point enters the queue more than N times, there is a negative loop (SPFA cannot handle negative loops picture)
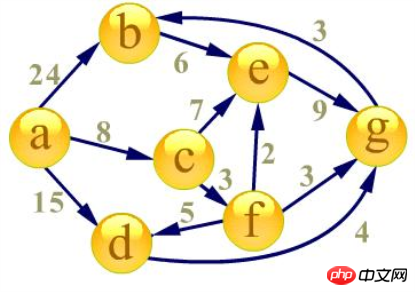
First establish the shortest
from the starting point a to the other points Path table
# 1. The first element (a) of the team is dequeued, and the relaxation operation is performed on the end points of all edges with a as the starting point (there are three points b, c, and d here). At this time, the path table status is: 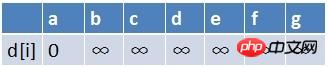
Point
needs to be added to the queue. At this time, three new nodes b, c, and d are added to the queue.
The first element of the team, point b, is dequeued. Relax the end points of all edges with b as the starting point in sequence (there is only point e here). At this time, the path table status is: 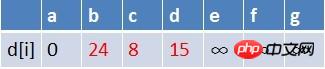
#In the shortest path table, the shortest path estimate of e has also become smaller. e does not exist in the queue, so e also has to
Enter the queue. At this time, the queue The elements in are c, d, e
The first element of the team is out of the team at point c, and the relaxation operation is performed on the end points of all edges with c as the starting point (here are e, f two points), at this time the path table status is:

## This is in the shortest path table, E, F's shortest path valuation has become smaller, E exists in the queue, F does not exist. Therefore
e does not need to join the queue, and f needs to join the queue. At this time, the elements in the queue are d, e, f
The first element d of the team is clicked out Team, perform relaxation operations on the end points of all edges with d as the starting point in sequence (there is only point g here). At this time, the path table status is:
Relaxation is unsuccessful), no new node enters the queue, the element in the queue is f, g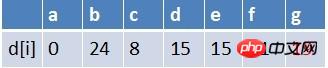
The first element of the team is dequeued at point f, and the end points of all edges with f as the starting point are sequentially Perform the relaxation operation (there are three points d, e, and g here). At this time, the path table status is:
## #In the shortest path table, the shortest path estimates of e and g become smaller again. There is no point e in the queue, and e joins the queue. There is a point g in the queue, and g does not need to join the queue. At this time, the elements in the queue are g, e
The first element of the team, point g, is dequeued, and the relaxation operation is performed on the end points of all edges with g as the starting point (there is only point b here). At this time, the path table status is: 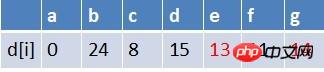
In the shortest path table, the shortest path estimate of b becomes smaller again, and there is no point b in the queue , b enters the queue. At this time, the element in the queue is e, and the first element of the team b
is dequeued at point e. The relaxation operation is performed on the end points of all edges with e as the starting point in sequence (only g here is This point), at this time the path table status is: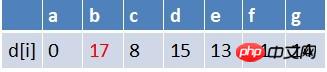
In the shortest path table, the shortest path estimate of g has not changed (relaxation is unsuccessful). At this time, the element in the queue is b
#In the shortest path table, the shortest path estimate of e has not changed (relaxation was unsuccessful), and the queue is empty at this time 
java code
package spfa负权路径;
import java.awt.List;
import java.util.ArrayList;
import java.util.Scanner;
public class SPFA {
/**
* @param args
*/
public long[] result; //用于得到第s个顶点到其它顶点之间的最短距离
//数组实现邻接表存储
class edge{
public int a;//边的起点
public int b;//边的终点
public int value;//边的值
public edge(int a,int b,int value){
this.a=a;
this.b=b;
this.value=value;
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
SPFA spafa=new SPFA();
Scanner scan=new Scanner(System.in);
int n=scan.nextInt();
int s=scan.nextInt();
int p=scan.nextInt();
edge[] A=new edge[p];
for(int i=0;i<p;i++){
int a=scan.nextInt();
int b=scan.nextInt();
int value=scan.nextInt();
A[i]=spafa.new edge(a,b,value);
}
if(spafa.getShortestPaths(n,s,A)){
for(int i=0;i<spafa.result.length;i++){
System.out.println(spafa.result[i]+" ");
}
}else{
System.out.println("存在负环");
}
}
/*
* 参数n:给定图的顶点个数
* 参数s:求取第s个顶点到其它所有顶点之间的最短距离
* 参数edge:给定图的具体边
* 函数功能:如果给定图不含负权回路,则可以得到最终结果,如果含有负权回路,则不能得到最终结果
*/
private boolean getShortestPaths(int n, int s, edge[] A) {
// TODO Auto-generated method stub
ArrayList<Integer> list = new ArrayList<Integer>();
result=new long[n];
boolean used[]=new boolean[n];
int num[]=new int[n];
for(int i=0;i<n;i++){
result[i]=Integer.MAX_VALUE;
used[i]=false;
}
result[s]=0;//第s个顶点到自身距离为0
used[s]=true;//表示第s个顶点进入数组队
num[s]=1;//表示第s个顶点已被遍历一次
list.add(s); //第s个顶点入队
while(list.size()!=0){
int a=list.get(0);//获取数组队中第一个元素
list.remove(0);//删除数组队中第一个元素
for(int i=0;i<A.length;i++){
//当list数组队的第一个元素等于边A[i]的起点时
if(a==A[i].a&&result[A[i].b]>(result[A[i].a]+A[i].value)){
result[A[i].b]=result[A[i].a]+A[i].value;
if(!used[A[i].b]){
list.add(A[i].b);
num[A[i].b]++;
if(num[A[i].b]>n){
return false;
}
used[A[i].b]=true;//表示边A[i]的终点b已进入数组队
}
}
}
used[a]=false; //顶点a出数组对
}
return true;
}
}
The above is the detailed content of SPFA algorithm usage tutorial. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undress AI Tool
Undress images for free

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)
 Detailed explanation of obtaining administrator rights in Win11
Mar 08, 2024 pm 03:06 PM
Detailed explanation of obtaining administrator rights in Win11
Mar 08, 2024 pm 03:06 PM
Windows operating system is one of the most popular operating systems in the world, and its new version Win11 has attracted much attention. In the Win11 system, obtaining administrator rights is an important operation. Administrator rights allow users to perform more operations and settings on the system. This article will introduce in detail how to obtain administrator permissions in Win11 system and how to effectively manage permissions. In the Win11 system, administrator rights are divided into two types: local administrator and domain administrator. A local administrator has full administrative rights to the local computer
 Detailed explanation of division operation in Oracle SQL
Mar 10, 2024 am 09:51 AM
Detailed explanation of division operation in Oracle SQL
Mar 10, 2024 am 09:51 AM
Detailed explanation of division operation in OracleSQL In OracleSQL, division operation is a common and important mathematical operation, used to calculate the result of dividing two numbers. Division is often used in database queries, so understanding the division operation and its usage in OracleSQL is one of the essential skills for database developers. This article will discuss the relevant knowledge of division operations in OracleSQL in detail and provide specific code examples for readers' reference. 1. Division operation in OracleSQL
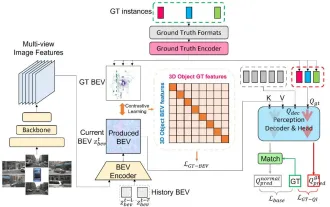 CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
Written above & the author’s personal understanding: At present, in the entire autonomous driving system, the perception module plays a vital role. The autonomous vehicle driving on the road can only obtain accurate perception results through the perception module. The downstream regulation and control module in the autonomous driving system makes timely and correct judgments and behavioral decisions. Currently, cars with autonomous driving functions are usually equipped with a variety of data information sensors including surround-view camera sensors, lidar sensors, and millimeter-wave radar sensors to collect information in different modalities to achieve accurate perception tasks. The BEV perception algorithm based on pure vision is favored by the industry because of its low hardware cost and easy deployment, and its output results can be easily applied to various downstream tasks.
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Can artificial intelligence predict crime? Explore CrimeGPT's capabilities
Mar 22, 2024 pm 10:10 PM
Can artificial intelligence predict crime? Explore CrimeGPT's capabilities
Mar 22, 2024 pm 10:10 PM
The convergence of artificial intelligence (AI) and law enforcement opens up new possibilities for crime prevention and detection. The predictive capabilities of artificial intelligence are widely used in systems such as CrimeGPT (Crime Prediction Technology) to predict criminal activities. This article explores the potential of artificial intelligence in crime prediction, its current applications, the challenges it faces, and the possible ethical implications of the technology. Artificial Intelligence and Crime Prediction: The Basics CrimeGPT uses machine learning algorithms to analyze large data sets, identifying patterns that can predict where and when crimes are likely to occur. These data sets include historical crime statistics, demographic information, economic indicators, weather patterns, and more. By identifying trends that human analysts might miss, artificial intelligence can empower law enforcement agencies
 Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
The bottom layer of the C++sort function uses merge sort, its complexity is O(nlogn), and provides different sorting algorithm choices, including quick sort, heap sort and stable sort.
 Detailed explanation of the role and usage of PHP modulo operator
Mar 19, 2024 pm 04:33 PM
Detailed explanation of the role and usage of PHP modulo operator
Mar 19, 2024 pm 04:33 PM
The modulo operator (%) in PHP is used to obtain the remainder of the division of two numbers. In this article, we will discuss the role and usage of the modulo operator in detail, and provide specific code examples to help readers better understand. 1. The role of the modulo operator In mathematics, when we divide an integer by another integer, we get a quotient and a remainder. For example, when we divide 10 by 3, the quotient is 3 and the remainder is 1. The modulo operator is used to obtain this remainder. 2. Usage of the modulo operator In PHP, use the % symbol to represent the modulus
 Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
1. Background of the Construction of 58 Portraits Platform First of all, I would like to share with you the background of the construction of the 58 Portrait Platform. 1. The traditional thinking of the traditional profiling platform is no longer enough. Building a user profiling platform relies on data warehouse modeling capabilities to integrate data from multiple business lines to build accurate user portraits; it also requires data mining to understand user behavior, interests and needs, and provide algorithms. side capabilities; finally, it also needs to have data platform capabilities to efficiently store, query and share user profile data and provide profile services. The main difference between a self-built business profiling platform and a middle-office profiling platform is that the self-built profiling platform serves a single business line and can be customized on demand; the mid-office platform serves multiple business lines, has complex modeling, and provides more general capabilities. 2.58 User portraits of the background of Zhongtai portrait construction