HTML5 Advanced Programming Graphic Distortion and Its Application 3 (Extended)

This article is the third in the series. The first two articles introduce the principle of achieving image distortion effect in HTML5, as well as the detailed usage of the drawtriangles function,

Let’s take a look at the extension of the drawtriangles function. Use the drawtriangles function to realize a rotated 3D Earth. The effect is as follows

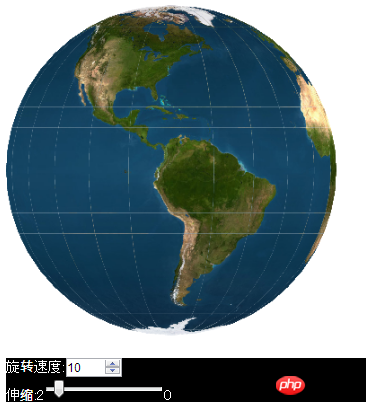
Because there is a bug in the drawtriangles function of version 1.5.0 of lufylegend, I quietly updated version 1.5.1 of lufylegend. You can download it from the official website at the following address:

http: //lufylegend.com/lufylegend

In fact, to draw the 3D sphere effect, first draw a plane, then divide the plane into small triangles, and then use these small triangles to piece together a sphere.

Now, I first create a blank LBitmapData object, and then divide this object into N small triangles. For specific methods, see the code below

earthBitmapData = new LBitmapData("#ffffff", 0, 0, 500, 300);
var i, j;
vertices = new Array();
for(i=0;i<=cols;i++){
	for(j=0;j<=rows;j++){
		vertices.push(i*15,j*15);
	}
}
indices = new Array();
for (i = 0; i < cols; i++) {
	for (j = 0; j < rows; j++) {
		indices.push(i * (rows + 1) + j, (i + 1) * (rows + 1) + j, i * (rows + 1) + j + 1);
		indices.push((i + 1) * (rows + 1) + j, i * (rows + 1) + j + 1, (i + 1) * (rows + 1) + j + 1);
	}
}
uvtData = new Array();
for (i = 0; i <= cols; i++) {
	for (j = 0; j <= rows; j++) {
		uvtData.push(i / cols, j / rows);
	}
}

Then, use the drawtriangles function to draw the LBitmapData object Go to the screen

backLayer = new LSprite();
addChild(backLayer);
backLayer.graphics.clear();
backLayer.graphics.beginBitmapFill(earthBitmapData);
backLayer.graphics.drawTriangles(vertices, indices, uvtData, 2);

and get the effect as shown below.

If you want to program this plane into a circle, you need to calculate the coordinates of each small triangle in the picture. Let's first look at how the y coordinate should be calculated. See The picture below is a vertical section of a ball

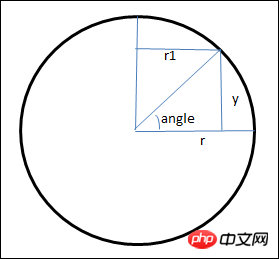
Use trigonometric functions to calculate the y coordinate in the picture and the horizontal section of the ball at the location of the y coordinate. The radius of the circle r1

var a = Math.sin(angle);
if((90-180*j/rows)%90==0 && (90-180*j/rows)%180!=0)a=(90-180*j/rows)>0?1:-1;
var y =  -r*a;
var sa = Math.cos(angle);
var r1 =  Math.abs(r*sa);

So, first bring the calculated y coordinate into the vertices array

for(i=0;i<=cols;i++){
	for(j=0;j<=rows;j++){
		var angle = (90-180*j/rows)*Math.PI/180;
		var a = Math.sin(angle);
		if((90-180*j/rows)%90==0 && (90-180*j/rows)%180!=0)a=(90-180*j/rows)>0?1:-1;
		if((90-180*j/rows)%180==0)a=0;
		var sy =  -r*a;
		vertices.push(i*15,sy);
	}
}

Because the x coordinate has not been calculated yet, a special figure is obtained, as follows

Next, let’s see how the coordinate of x is calculated. First, take out the plane section with radius r1, as shown below

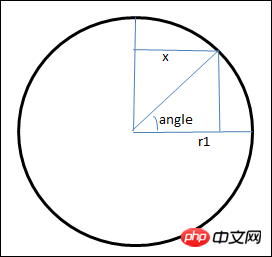
Use trigonometric functions to calculate the x coordinate in the graph

var b = Math.cos(angle*Math.PI/180);
var x =  r1*b;

At this time, if only the calculated x coordinate is brought into the vertices array

for(i=0;i<=cols;i++){
	for(j=0;j<=rows;j++){
		var sa = Math.cos(angle);
		if((90-180*j/rows)%180==0)sa=1;
		var sr =  Math.abs(r*sa);
		var angle2 = 360*(i+1)/cols;
		var b = Math.cos(angle2*Math.PI/180);
		if(angle2%360==0)b=1;
		else if(angle2%180==0)b=-1;
		var sx =  sr*b;
		vertices.push(sx,j*15);
	}
}

because The y coordinate is not calculated, so a very interesting graph is obtained, as follows

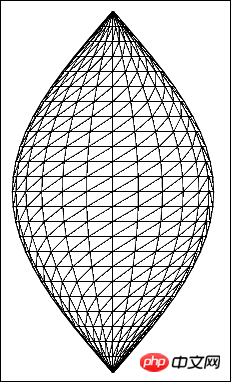
If the calculated x coordinate and y coordinate are brought into the vertices array at the same time If

for(i=0;i<=cols;i++){
	for(j=0;j<=rows;j++){
		var angle = (90-180*j/rows)*Math.PI/180;
		var a = Math.sin(angle);
		if((90-180*j/rows)%90==0 && (90-180*j/rows)%180!=0)a=(90-180*j/rows)>0?1:-1;
		if((90-180*j/rows)%180==0)a=0;
		var sy =  -r*a;
		var sa = Math.cos(angle);
		if((90-180*j/rows)%180==0)sa=1;
		var sr =  Math.abs(r*sa);
		var angle2 = 360*(i+1)/cols;
		var b = Math.cos(angle2*Math.PI/180);
		if(angle2%360==0)b=1;
		else if(angle2%180==0)b=-1;
		var sx =  sr*b;
		vertices.push(sx, sy);
	}
}

, you will get a complete sphere graphic, as shown below

The next step is simple, replace the blank picture with the plane diagram of the earth, The code is as follows

earthBitmapData = new LBitmapData(imglist["earth"]);

Run the code again, you can get the following 3D graphics

Now, it’s time to let the earth rotate. According to As mentioned in the previous article, the elements in the uvtData array passed into the drawtriangles function are the relative positions of each small triangle in the original picture. They determine the starting position of drawing the picture. If a set of positions, such as 0123, is changed, the positions It becomes 1230, and then continues to transform into 2301. By continuously changing the position in this way, visually, the rotation has actually been realized. Then in the code, you only need to move the divided array according to each column, each time Move the two sets of triangles in the first column to the last column, so that the two sets of triangles in the second column become the first column, so that constant transformation can make an earth rotate

for (i = 0; i <= rows; i++) {
	uvtData.push(uvtData.shift());
	uvtData.push(uvtData.shift());
}

If you want Changing the size of the earth is even simpler. Changing the scaleX and scaleY properties of the LSprite object can change its size. You can click on the link below to test its effect

http:/ /lufy.netne.net/lufylegend-js/3dearth/index.html

Remarks:

Once again, the content introduced in this article requires the support of version 1.5.1 or above of the HTML5 open source engine lufylegend. The release address of lufylegend version 1.5.1 is as follows

http://lufylegend.com /lufylegend

The above is the content of HTML5 Advanced Programming Graphic Distortion and Its Application III (Extension). For more related content, please pay attention to the PHP Chinese website (m.sbmmt.com)!