Algorithm summary of Photoshop Gaussian blur filter-PS Tutorial-php.cn

Algorithm summary of Photoshop Gaussian blur filter

高洛峰

Release： 2017-02-20 09:40:35

Original

1875 people have browsed it

recently felt that some netizens' research on Gaussian blur filter is now summarized as follows. Gaussian blur is a kind of digital image template processing method. Its template is calculated based on a two-dimensional normal distribution (Gaussian distribution) function.
The normal distribution was first obtained by A. Demoivre in finding the asymptotic formula of the binomial distribution. C.F. Gauss derived it from another angle when studying measurement error. P.S. Laplace and Gauss studied its properties. Hence the name Gaussian blur.

Function definition of one-dimensional normal distribution:

Distribution of type random variables, the first parameter μ is the mean value of the random variable that follows the normal distribution , the second parameter σ2 is the variance of this random variable, so the normal distribution is recorded as N(μ, σ2). The probability rule of a random variable that follows a normal distribution is that the probability of taking a value near μ is high, and the probability of taking a value that is farther away from μ is smaller; the smaller σ, the more concentrated the distribution is near μ, and the larger σ, the smaller the distribution. dispersion. The characteristics of the density function of the normal distribution are: symmetric about μ, reaching a maximum value at μ, taking a value of 0 at positive (negative) infinity, and having an inflection point at μ±σ. Its shape is high in the middle and low on both sides, and the image is a bell-shaped curve above the x-axis. When μ = 0, σ2 = 1, it is called the standard normal distribution, recorded as N (0, 1). 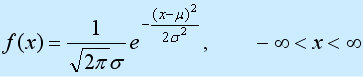Algorithm summary of Photoshop Gaussian blur filter

The meaning of the two constants: μ-expectation, σ^2 variance.

Below we solve the first question: What is the radius in the Gaussian blur filter? The answer is that the Gaussian radius is σ in the formula.

’ ’ s ’ ’ s ’ s ’ s ’ ’ ’ ’ s ’ ’ s ’ ’ s ’ s ’ s ‐ ‐ ‐ ‑ ‐ # It can be seen that the Gaussian radius (σ) affects the shape of the curve. The smaller the σ, the higher and sharper the curve. The larger the σ, the lower and gentler the curve. For a two-dimensional image, it is a bell-shaped surface. The smaller the Gaussian radius, the higher, sharper, and steeper the surface; the larger the Gaussian radius, the lower and gentler the surface. Therefore, the smaller the Gaussian radius, the smaller the blur, and the larger the Gaussian radius, the greater the blur. We will see that ps defines the range of Gaussian radius as [0.1~250]. When the radius is 0.1, only the middle pixel of the Gaussian template is 1 after calculation, and the other pixels are all = 0 (actually just approaching 0), that is, the image will not change.

The second question is, what is the relationship between Gaussian template size and Gaussian radius? This is a misunderstanding that has always troubled us. Because our thinking has entered the misunderstanding of physical implementation. In the physical implementation, the Gaussian template is bounded, causing us to ignore the real answer to this question: the Gaussian template is logically unbounded. That is to say, the Gaussian template is essentially an approximation of a logically infinite extended surface. Therefore, the template size should be considered infinite. It's just that during calculation, because it approaches 0 in the distance, we no longer consider these values below a certain threshold. This threshold is the template boundary.

Below, the formula of the two -dimensional Gaussian surface (x, y represents the template coordinates of pixels, the center position of the template is the origin):

Algorithm summary of Photoshop Gaussian blur filter

That is: g(x,y)= ( 1 / (2*pi*σ^2) ) * exp( -(x^2+y^2)/(2*σ^2 ) ) ;

Based on this formula, we can calculate the Gaussian templates under different radii. In fact, the templates are infinite, but they will approach 0 far away from the center. For example, we calculate r A normalized Gaussian template when =0.7:

高斯模板（guass radius=0.700000）

在网络上众所周知流传的高斯3*3模板实际上是对高斯曲面的一个整数除法形式的近似：

1 2 1

2 4 2 /16

1 2 1

Actual verification, we found that this 3*3 template is actually an approximation of the Gaussian radius when it is about 0.849. When r=0.849, its 3*3 normalized template is (in MATLAB, enter h=fspecial('gaussian', 3, 0.849);You can get this template): 0.062467 0.125000 0.062467

0.125000 0.250131 0.125000

0.062467 0.125000 0.06246 7## Then we can use imfilter in Matlab to perform Gaussian blur processing on the image:

img = imread('c:\demo.bmp'); h = fspecial('gaussian', 3, 0.849);

img2 = imfilter(img, h) ;

subplot(121), imshow(img); title('Original image')

subplot(122), imshow(img2); title('After Gaussian blur')

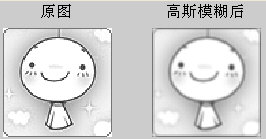
# The effect is as follows: We can use it in Matlab as follows Statement to draw Gaussian surface:

Matlab code for drawing Gaussian surface

Algorithm summary of Photoshop Gaussian blur filter

Code highlighting produced by Actipro CodeHighlighter (freeware)

http:/ /m.sbmmt.com/

-->%Draw a Gaussian blur surface!

#include math.h>include
stdio.h>
define## N 3 3 / * Template size: (2N+1) * (2N+1) */
void main(){

double a[2*N+1][2*N+1]; /* Gaussian template*/ /* Gaussian radius: [0.1, 250] */
double A=1/
(2*##M_PI*r*r); int i,j; for(i=-
1*
N;i N;i++) for(j=-1 *N;j
N;j++)a[i+N][j+N]=A *exp((-1)*(i*i+j*j)/ (2*r*r));
}

## At the same time, as a comparison, we give the code to generate a Gaussian template in Matlab (the code part of fspecial, where p3 is the third parameter That is Gaussian radius):

  case &#39;gaussian&#39; % Gaussian filter

     siz   = (p2-1)/2;  %注：p2即模板边长，默认值为33
     std   = p3;        %注：p3即高斯半径，默认为为0.5
     
     [x,y] = meshgrid(-siz(2):siz(2),-siz(1):siz(1));
     arg   = -(x.*x + y.*y)/(2*std*std);

     h     = exp(arg);
     h(h<eps*max(h(:))) = 0;

     sumh = sum(h(:));  %注：模板归一化
     if sumh ~= 0,
       h  = h/sumh;
     end;

Copy after login

For more related articles on the algorithm summary of Photoshop Gaussian blur filter, please pay attention to the PHP Chinese website!