The Eight Queens problem is to find a solution to place a queen in each row on a chessboard such that no two queens can attack each other. The problem can be solved using recursion. In this section, we will introduce a common algorithm design technique called backtracking for solving this problem. The backtracking approach searches for a candidate solution incrementally, abandoning that option as soon as it determines that the
candidate cannot possibly be a valid solution, and then looks for a new candidate.
You can use a two-dimensional array to represent a chessboard. However, since each row can have only one queen, it is sufficient to use a one-dimensional array to denote the position of the queen in the row. Thus, you can define the queens array as:
int[] queens = new int[8];
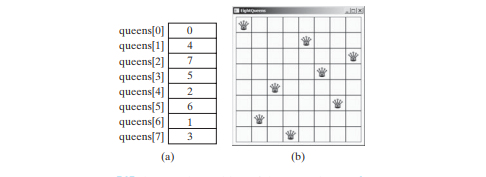
Assign j to queens[i] to denote that a queen is placed in row i and column j. Figure below (a) shows the contents of the queens array for the chessboard in Figure below (b).
The search starts from the first row with k = 0, where k is the index of the current row being considered. The algorithm checks whether a queen can be possibly placed in the j_th column in the row for _j = 0, 1, ... , 7, in this order. The search is implemented as follows:
The code below gives the program that displays a solution for the Eight Queens problem.
package application;
import javafx.application.Application;
import javafx.geometry.Pos;
import javafx.stage.Stage;
import javafx.scene.Scene;
import javafx.scene.control.Label;
import javafx.scene.image.Image;
import javafx.scene.image.ImageView;
import javafx.scene.layout.GridPane;
public class EightQueens extends Application {
public static final int SIZE = 8; // The size of the chess board
// queens are placed at (i, queens[i])
// -1 indicates that no queen is currently placed in the ith row
// Initially, place a queen at (0, 0) in the 0th row
private int[] queens = {-1, -1, -1, -1, -1, -1, -1, -1};
@Override // Override the start method in the Application class
public void start(Stage primaryStage) {
search(); // Search for a solution
// Display chess board
GridPane chessBoard = new GridPane();
chessBoard.setAlignment(Pos.CENTER);
Label[][] labels = new Label[SIZE][SIZE];
for(int i = 0; i < SIZE; i++)
for(int j = 0; j < SIZE; j++) {
chessBoard.add(labels[i][j] = new Label(), i, j);
labels[i][j].setStyle("-fx-border-color: black");
labels[i][j].setPrefSize(55, 55);
}
// Display queens
Image image = new Image("file:C:/Users/Paul/development/MyJavaFX/src/application/image/lo.jpg");
for(int i = 0; i < SIZE; i++)
labels[i][queens[i]].setGraphic(new ImageView(image));
// Create a scene and place it in the stage
Scene scene = new Scene(chessBoard, 55 * SIZE, 55 * SIZE);
primaryStage.setTitle("EightQueens"); // Set the stage title
primaryStage.setScene(scene); // Place the scene in the stage
primaryStage.show(); // Display the stage
}
public static void main(String[] args) {
Application.launch(args);
}
/** Search for a solution */
private boolean search() {
// k - 1 indicates the number of queens placed so far
// We are looking for a position in the kth row to place a queen
int k = 0;
while(k >= 0 && k < SIZE) {
// Find a position to place a queen in the kth row
int j = findPosition(k);
if(j < 0) {
queens[k] = -1;
k--; // back track to the previous row
} else {
queens[k] = j;
k++;
}
}
if(k == -1)
return false; // No solution
else
return true; // A solution is found
}
public int findPosition(int k) {
int start = queens[k] + 1; // Search for a new placement
for(int j =start; j < SIZE; j++) {
if(isValid(k, j))
return j; // (k, j) is the place to put the queen now
}
return -1;
}
/** Return true is a queen can be placed at (row, column) */
public boolean isValid(int row, int column) {
for(int i = 1; i <= row; i++)
if(queens[row - i] == column // Check column
|| queens[row - i] == column - i // Check upleft diagonal
|| queens[row - i] == column + i) // Check upright diagonal
return false; // There is a conflict
return true; // No conflict
}
}
The program invokes search() (line 20) to search for a solution. Initially, no queens are placed in any rows (line 16). The search now starts from the first row with k = 0 (line 53) and finds a place for the queen (line 56). If successful, place it in the row (line 61) and consider the next row (line 62). If not successful, backtrack to the previous row (lines 58–59).
The findPosition(k) method searches for a possible position to place a queen in row k starting from queen[k] + 1 (line 73). It checks whether a queen can be placed at start, start + 1, . . . , and 7, in this order (lines 75–78). If possible, return the column index (line 77); otherwise, return -1 (line 80).
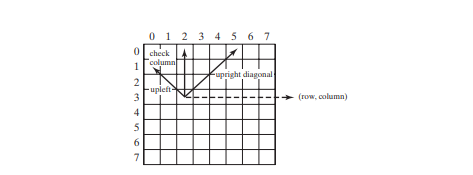
The isValid(row, column) method is called to check whether placing a queen at the specified position causes a conflict with the queens placed earlier (line 76). It ensures that no queen is placed in the same column (line 86), in the upper-left diagonal (line 87), or in the upper-right diagonal (line 88), as shown in Figure below.
The above is the detailed content of Solving the Eight Queens Problem Using Backtracking. For more information, please follow other related articles on the PHP Chinese website!
![[Web front-end] Node.js quick start](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
