The AIxiv column is a column where this site publishes academic and technical content. In the past few years, the AIxiv column of this site has received more than 2,000 reports, covering top laboratories from major universities and companies around the world, effectively promoting academic exchanges and dissemination. If you have excellent work that you want to share, please feel free to contribute or contact us for reporting. Submission email: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com
The authors of this paper are from Huawei’s Montreal Noah’s Ark Laboratory Kang Jikun, Li Xinze, Chen Xi, Amirreza Kazemi, and Chen Boxing. Artificial intelligence (AI) has made great progress in the past decade, especially in the fields of natural language processing and computer vision. However, how to improve AI’s cognitive capabilities and reasoning capabilities remains a huge challenge. Recently, a paper titled "MindStar: Enhancing Math Reasoning in Pre-trained LLMs at Inference Time" proposed a tree search-based inference time capability improvement method MindStar [1], which is implemented in the open source model Llama -13-B and Mistral-7B have achieved the reasoning capabilities of approximate closed-source large models GPT-3.5 and Grok-1 on mathematical problems. 
- Paper title: MindStar: Enhancing Math Reasoning in Pre-trained LLMs at Inference Time
- Paper address: https://arxiv.org/abs/2405.16265v2
MindStar Application effect on mathematical issues: 
Figure 1: Mathematical accuracy of different large -scale language models. LLaMA-2-13B is similar in mathematical performance to GPT-3.5 (4-shot) but saves approximately 200 times more computational resources. Introduction Impressive results have been demonstrated in areas such as ,and creative writing [5]. However, unlocking the ability of LLMs to solve complex reasoning tasks remains a challenge. Some recent studies [6,7] try to solve the problem through supervised fine-tuning (SFT). By mixing new inference data samples with the original data set, LLMs learn the underlying distribution of these samples and try to imitate the underlying distribution. Learn logic to solve unseen reasoning tasks. Although this approach has performance improvements, it relies heavily on extensive training and additional data preparation [8,9].
The Llama-3 report [10] highlights an important observation: when faced with a challenging inference problem, models sometimes generate correct inference trajectories. This suggests that the model knows how to produce the correct answer, but is having trouble selecting it. Based on this finding, we asked a simple question: Can we enhance the reasoning capabilities of LLMs by helping them choose the right output? To explore this, we conducted an experiment utilizing different reward models for LLMs output selection. Experimental results show that step-level selection significantly outperforms traditional CoT methods. Figure 2 Algorithm architecture diagram of MindStar We introduce a new inference search framework - MindStar (M*), by treating the inference task as a search problem and leveraging the rewards of process supervision Model (Process-supervised Reward Model, PRM), M * effectively navigates in the inference tree space and identifies approximately optimal paths. Combining the ideas of Beam Search (BS) and Levin Tree Search (LevinTS), the search efficiency is further enhanced and the optimal reasoning path is found within limited computational complexity. 2.1 Process Supervised Reward Model The Process Supervised Reward Model (PRM) is designed to evaluate the intermediate steps of large language model (LLM) generation to help select the correct inference path. This approach builds on the success of PRM in other applications. Specifically, PRM takes the current reasoning path 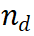 and the potential next step
and the potential next step 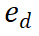 as input, and returns a reward value
as input, and returns a reward value 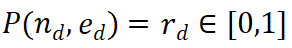 . PRM evaluates new steps by considering the entire current reasoning trajectory, encouraging consistency and fidelity to the overall path. A high reward value indicates that the new step
. PRM evaluates new steps by considering the entire current reasoning trajectory, encouraging consistency and fidelity to the overall path. A high reward value indicates that the new step 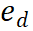 ) is likely to be correct for a given reasoning path
) is likely to be correct for a given reasoning path 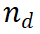 , making the expansion path worth further exploration. Conversely, a low reward value indicates that the new step may be incorrect, which means that the solution following this path may also be incorrect. The M* algorithm consists of two main steps, iterating until the correct solution is found: 1. Inference path expansion: In each iteration, the underlying LLM generates the next step of the current inference path. 2. Evaluation and selection: Use PRM to evaluate the generated steps and select the inference path for the next iteration based on these evaluations. 2.2 Inference path expansion
, making the expansion path worth further exploration. Conversely, a low reward value indicates that the new step may be incorrect, which means that the solution following this path may also be incorrect. The M* algorithm consists of two main steps, iterating until the correct solution is found: 1. Inference path expansion: In each iteration, the underlying LLM generates the next step of the current inference path. 2. Evaluation and selection: Use PRM to evaluate the generated steps and select the inference path for the next iteration based on these evaluations. 2.2 Inference path expansion
After selecting the inference path to extend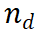 , we designed a prompt template (Example 3.1) to collect the next steps from the LLM. As the example shows, LLM treats the original question as {question} and the current reasoning path as {answer}. Note that in the first iteration of the algorithm, the selected node is the root node that contains only the question, so {answer} is empty. For an inference path
, we designed a prompt template (Example 3.1) to collect the next steps from the LLM. As the example shows, LLM treats the original question as {question} and the current reasoning path as {answer}. Note that in the first iteration of the algorithm, the selected node is the root node that contains only the question, so {answer} is empty. For an inference path  , LLM generates N intermediate steps and appends them as children of the current node. In the next step of the algorithm, these newly generated child nodes are evaluated and a new node is selected for further expansion. We also realized that another way to generate steps is to fine-tune the LLM using step markers. However, this may reduce the inference ability of LLM, and more importantly, it goes against the focus of this article - to enhance the inference ability of LLM without modifying the weights. 2.3 Inference path selection After expanding the inference tree, we use a pre-trained procedural supervised reward model (PRM) to evaluate each newly generated step. As mentioned earlier, PRM takes a path and a step , and returns the corresponding reward value. After evaluation, we need a tree search algorithm to select the next node to expand. Our framework does not rely on a specific search algorithm, and in this work we instantiate two best-first search methods, namely Beam Search and Levin Tree Search. 3. Results and Discussion Extensive evaluation on GSM8K and MATH datasets shows that M* significantly improves the inference capabilities of open source models (such as LLaMA-2), and its performance is comparable to It is comparable to larger closed-source models (such as GPT-3.5 and Grok-1), while significantly reducing model size and computational cost. These findings highlight the potential of shifting computational resources from fine-tuning to inference-time search, opening new avenues for future research into efficient inference enhancement techniques.
, LLM generates N intermediate steps and appends them as children of the current node. In the next step of the algorithm, these newly generated child nodes are evaluated and a new node is selected for further expansion. We also realized that another way to generate steps is to fine-tune the LLM using step markers. However, this may reduce the inference ability of LLM, and more importantly, it goes against the focus of this article - to enhance the inference ability of LLM without modifying the weights. 2.3 Inference path selection After expanding the inference tree, we use a pre-trained procedural supervised reward model (PRM) to evaluate each newly generated step. As mentioned earlier, PRM takes a path and a step , and returns the corresponding reward value. After evaluation, we need a tree search algorithm to select the next node to expand. Our framework does not rely on a specific search algorithm, and in this work we instantiate two best-first search methods, namely Beam Search and Levin Tree Search. 3. Results and Discussion Extensive evaluation on GSM8K and MATH datasets shows that M* significantly improves the inference capabilities of open source models (such as LLaMA-2), and its performance is comparable to It is comparable to larger closed-source models (such as GPT-3.5 and Grok-1), while significantly reducing model size and computational cost. These findings highlight the potential of shifting computational resources from fine-tuning to inference-time search, opening new avenues for future research into efficient inference enhancement techniques. 
Table 1 shows the comparison results of various schemes on the GSM8K and MATH inference benchmarks. The number for each entry indicates the percentage of problem solved. The notation SC@32 represents self-consistency among 32 candidate results, while n-shot represents the results on few-shot examples. CoT-SC@16 refers to self-consistency among 16 Chain of Thought (CoT) candidate results. BS@16 represents the beam search method, which involves 16 candidate results at each step level, while LevinTS@16 details the Levin tree search method using the same number of candidate results. It is worth noting that the latest result for GPT-4 on the MATH dataset is GPT-4-turbo-0409, which we particularly emphasize as it represents the best performance in the GPT-4 family. 
Figure 3 We study how M* performance changes as the number of step-level candidates changes. We selected Llama-2-13B as the base model and beam search (BS) as the search algorithm, respectively. 
Figure 4 Scaling laws of the Llama-2 and Llama-3 model families on the MATH data set. All results are derived from their original sources. We use Scipy tools and logarithmic functions to calculate the fitted curves. 
Table 2 Average number of tokens produced by different methods when answering questionsThis paper introduces MindStar (M*), a novel search-based reasoning framework for Enhance the inference capabilities of pre-trained large language models. By treating the inference task as a search problem and leveraging a reward model of process supervision, M* efficiently navigates in the inference tree space, identifying near-optimal paths. Combining the ideas of beam search and Levin tree search further enhances the search efficiency and ensures that the best reasoning path can be found within limited computational complexity. Extensive experimental results show that M* significantly improves the inference capabilities of open source models, and its performance is comparable to larger closed source models, while significantly reducing model size and computational costs. These research results show that shifting computing resources from fine-tuning to inference-time search has great potential, opening up new avenues for future research on efficient inference enhancement technologies. [1] Nisan Stiennon, Long Ouyang, Jeffrey Wu, Daniel Ziegler, Ryan Lowe, Chelsea Voss, Alec Radford, Dario Amodei, and Paul F Christiano. Learning to summarize with human feedback. Advances in Neural Information Processing Systems, 33:3008–3021, 2020.[2] Long Ouyang, Jeffrey Wu, Xu Jiang, Diogo Almeida, Carroll Wainwright, Pamela Mishkin, Chong Zhang, Sandhini Agarwal, Katarina Slama, Alex Ray, et al. Training language models to follow instructions with human feedback. Advances in neural information processing systems, 35:27730–27744, 2022. [3] Ziyang Luo, Can Xu, Pu Zhao, Qingfeng Sun, Xiubo Geng, Wenxiang Hu, Chongyang Tao, Jing Ma, Qingwei Lin, and Daxin Jiang. Wizardcoder: Empowering code large language models with evol-instruct. arXiv preprint arXiv:2306.08568, 2023. [4] Mark Chen, Jerry Tworek, Heewoo Jun, Qiming Yuan, Henrique Ponde de Oliveira Pinto, Jared Kaplan, Harri Edwards, Yuri Burda, Nicholas Joseph, Greg Brockman, et al. Evaluating large language models trained on code. arXiv preprint arXiv:2107.03374, 2021.[5] Carlos Gómez-Rodríguez and Paul Williams. A confederacy of models: A comprehensive evaluation of llms on creative writing. arXiv preprint arXiv:2310.08433, 2023. [6] Longhui Yu, Weisen Jiang, Han Shi, Jincheng Yu, Zhengying Liu, Yu Zhang, James T Kwok, Zhenguo Li, Adrian Weller, and Weiyang Liu. Metamath: Bootstrap your own mathematical questions for large language models. arXiv preprint arXiv:2309.12284, 2023. [7] Zhihong Shao, Peiyi Wang, Qihao Zhu, Runxin Xu, Junxiao Song, Mingchuan Zhang, YK Li, Y Wu, and Daya Guo. Deepseekmath: Pushing the limits of mathematical reasoning in open language models. arXiv preprint arXiv:2402.03300, 2024.[8] Keiran Paster, Marco Dos Santos, Zhangir Azerbayev, and Jimmy Ba. Openwebmath: An open dataset of high-quality mathematical web text. arXiv preprint arXiv:2310.06786, 2023.[9] Peiyi Wang, Lei Li, Zhihong Shao, RX Xu, Damai Dai, Yifei Li, Deli Chen, Y Wu, and Zhifang Sui. Math-shepherd : Verify and reinforce llms step-by-step without human annotations. CoRR, abs/2312.08935, 2023.[10] Meta AI. Introducing meta llama 3: The most capable openly available llm to date, April 2024 . URL https://ai.meta.com/blog/meta-llama-3/. Accessed: 2024-04-30.The above is the detailed content of Can't wait for OpenAI's Q*, Huawei Noah's secret weapon MindStar to explore LLM reasoning is here first. For more information, please follow other related articles on the PHP Chinese website!




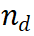 and the potential next step
and the potential next step 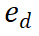 as input, and returns a reward value
as input, and returns a reward value 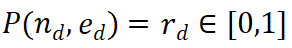 .
. 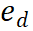 ) is likely to be correct for a given reasoning path
) is likely to be correct for a given reasoning path 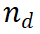 , making the expansion path worth further exploration. Conversely, a low reward value indicates that the new step may be incorrect, which means that the solution following this path may also be incorrect. The
, making the expansion path worth further exploration. Conversely, a low reward value indicates that the new step may be incorrect, which means that the solution following this path may also be incorrect. The 
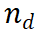 , we designed a prompt template (Example 3.1) to collect the next steps from the LLM. As the example shows, LLM treats the original question as {question} and the current reasoning path as {answer}. Note that in the first iteration of the algorithm, the selected node is the root node that contains only the question, so {answer} is empty. For an inference path
, we designed a prompt template (Example 3.1) to collect the next steps from the LLM. As the example shows, LLM treats the original question as {question} and the current reasoning path as {answer}. Note that in the first iteration of the algorithm, the selected node is the root node that contains only the question, so {answer} is empty. For an inference path  , LLM generates N intermediate steps and appends them as children of the current node. In the next step of the algorithm, these newly generated child nodes are evaluated and a new node is selected for further expansion. We also realized that another way to generate steps is to fine-tune the LLM using step markers. However, this may reduce the inference ability of LLM, and more importantly, it goes against the focus of this article - to enhance the inference ability of LLM without modifying the weights.
, LLM generates N intermediate steps and appends them as children of the current node. In the next step of the algorithm, these newly generated child nodes are evaluated and a new node is selected for further expansion. We also realized that another way to generate steps is to fine-tune the LLM using step markers. However, this may reduce the inference ability of LLM, and more importantly, it goes against the focus of this article - to enhance the inference ability of LLM without modifying the weights. 







