Insgesamt10000 bezogener Inhalt gefunden
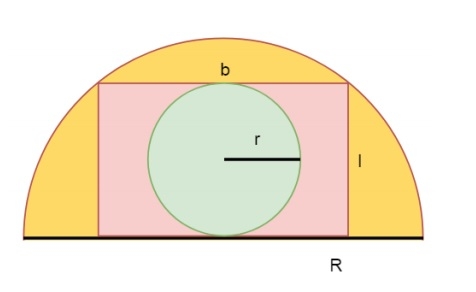
Wie groß ist die Fläche eines Kreises innerhalb eines Rechtecks, das in einen Halbkreis eingeschrieben ist?
Artikeleinführung:Betrachten wir einen gegebenen Halbkreis. Sein Radius ist R. In den Halbkreis ist ein Rechteck der Länge l und der Breite b eingeschrieben. In das Rechteck ist nun ein Kreis mit dem Radius r eingeschrieben. Wir müssen die Fläche des inneren Kreises finden. Wir wissen, dass die Länge des größten in einen Halbkreis eingeschriebenen Rechtecks l und die Breite b ist, dann lauten die Gleichungen von l und b wie folgt: Nun ist der Radius des größten Kreises, der in ein Rechteck eingeschrieben werden kann, r als folgt -
2023-09-04
Kommentar 0
1699
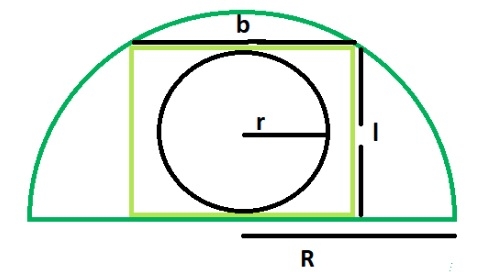
Wie groß ist die Fläche eines Kreises innerhalb eines Rechtecks, das in einen Halbkreis eingeschrieben ist?
Artikeleinführung:Ein in ein Rechteck eingeschriebener Kreis tangiert die längere Seite des Rechtecks, d. h. seine Länge tangiert den Kreis. Ein in einen Halbkreis eingeschriebenes Rechteck berührt zwei Punkte auf dem Bogen des Halbkreises. Die Breite des Rechtecks entspricht dem Durchmesser des Kreises. Wenn R der Radius des Halbkreises ist. Die Länge des Rechtecks = √2R/2 Die Breite des Rechtecks = R/√2 Der Radius des eingeschriebenen Kreises beträgt r = b/2 = R/2√2 Mit dieser Formel können wir das in den Halbkreis eingeschriebene Rechteck berechnen Die Fläche eines Kreises, Fläche = (π*r2)=π*R/8 Beispieldemonstration #include<stdio.h>intmain(){&
2023-09-13
Kommentar 0
1806

Übersetzen Sie in einem C-Programm Folgendes ins Chinesische: Wie groß ist die Fläche des eingeschriebenen Kreises eines rechtwinkligen Dreiecks?
Artikeleinführung:Um die Fläche des Innenkreises eines rechtwinkligen Dreiecks zu ermitteln, haben wir die Formel zum Ermitteln des Radius eines rechtwinkligen Dreiecks, r=(P+B–H)/2. Gegeben sind P, B und H jeweils die Senkrechte, die Basis und die Hypotenuse eines rechtwinkligen Dreiecks. Die Fläche eines Kreises ist gegeben durch: Fläche = π*r2 wobei π = 22/7 oder 3,14 und r der Radius des Kreises ist. Daher wird die Fläche des inneren Kreises durch die folgende Formel angegeben: Fläche=π*((P+B–H)/2)2. Beispiel#include#definePI3.14159265intmain(){ floatarea,P=3,B=4,H=5; area=(P+B
2023-09-07
Kommentar 0
862


C-Programm zum Drucken der Flächen von Dreiecken, Quadraten, Kreisen, Rechtecken und Polygonen mithilfe von Switch-Case-Anweisungen
Artikeleinführung:Frage: Schreiben Sie ein Programm, um mithilfe von Switchcase die Flächen von Dreiecken, Quadraten, Kreisen, Rechtecken und Polygonen zu berechnen. Lösung Berechnen Sie die Fläche von Dreieck, Quadrat, Kreis, Rechteck und Polygon basierend auf der Fallnummer. Die Logik zum Ermitteln der Fläche eines Dreiecks lautet wie folgt: Eingabedreieck a, b, cs=(float)(a+b+c)/2;area=(float)(sqrt(s*(s-a)* (s-b)*(s-c)) );Die Logik zum Ermitteln der Fläche eines Quadrats lautet wie folgt: Geben Sie zur Laufzeit die Seitenlänge des Quadrats ein. area=(float)side*side Die Logik zum Ermitteln der Fläche eines Kreises lautet wie folgt: Geben Sie den Radius des Kreises während der Laufzeit ein: area=(float)3.14159*;
2023-09-14
Kommentar 0
1075

Wie groß ist im C-Programm die Fläche eines Kreises, der in eine Raute eingeschrieben ist?
Artikeleinführung:Hier sehen wir die Fläche eines Kreises, der in eine Raute eingeschrieben ist. Die Diagonalen der Raute sind „a“ bzw. „b“. Der Radius des Kreises beträgt h. Zwei Diagonalen bilden vier gleiche Dreiecke. Jedes Dreieck ist ein rechtwinkliges Dreieck, also ist ihre Fläche - Jede Seite der Raute ist die Hypotenuse - Daher ist die Fläche des Kreises - Beispiel#include<iostream>#include<cmath>usingnamespacestd;floatarea(floata,floatb ) { if(a<0||b<0)//ifthevaluesaren
2023-09-01
Kommentar 0
1224

Wie groß ist die Fläche eines Kreises, der in eine Raute eingeschrieben ist?
Artikeleinführung:Der eingeschriebene Kreis einer Raute tangiert ihre vier Seiten und vier Endpunkte. Die Seiten der Raute berühren den Kreis. Hier ist r der Radius, der mithilfe von a und der Diagonale des angegebenen Werts ermittelt wird. Nun ist das Flächendreieck AOB = ½*OA*OB = ½*AB*r (beide verwenden die Formel ½*b*h). ½*a/2*b/2=½*(√(a2/4+b2/4))*ra*b/8=√(a2+b2)*r/4r=a*b/2√(a2 +b2) Kreisfläche = π*r*r=π*(a2*b2)/4(a2support>+b2) Beispiel für die Diagonalen der Raute 5 und 10. Die Fläche beträgt 15,700000. Beispielcode. Echtzeitdemonstration #include<stdio.h>intma
2023-09-05
Kommentar 0
1356

Ausführliches Tutorial zum Zeichnen rotierender Dreiecke mit einem geometrischen Skizzenblock
Artikeleinführung:1. Zeichnen Sie mit dem Punktwerkzeug drei Punkte A, B und C. Wählen Sie drei Punkte aus, wählen Sie [Konstruktion] – [Bogen durch drei Punkte], und wählen Sie dann [Konstruktion] – [Innenbogen] – [Innensektor] aus. 2. Bestimmen Sie mit dem Punktwerkzeug den Mittelpunkt des Kreises. (Wenn sich der Punkt in der Mitte des Kreises befindet, werden die beiden Radien des Sektors hervorgehoben.) Verwenden Sie das Liniensegment-Werkzeug, um einen Radius OD des Sektors zu erstellen. Wählen Sie mit dem Punktwerkzeug einen Punkt auf dem Radius aus, wählen Sie diesen Punkt und den Radius aus und wählen Sie [Konstruktion] - [Vertikale Linie]. 3. Wählen Sie mit dem Punktwerkzeug einen Punkt E auf der vertikalen Linie aus und konstruieren Sie die Liniensegmente DE und OE. Wählen Sie die vertikale Linie, den vertikalen Fuß und die Innenseite der Fächerform aus und drücken Sie [Strg+H], um sie auszublenden. 4. Wählen Sie das Dreieck aus, kopieren Sie es und fügen Sie es zweimal ein. Platzieren Sie einen an Punkt A und einen an Punkt C. Ziehen Sie die Eckpunkte so, dass sie mit der Mitte des Kreises übereinstimmen. Wählen Sie Punkt D aus.
2024-04-16
Kommentar 0
1192
So zeichnen Sie eine Schmetterlingsanimation auf dem Geometric Sketchpad_Design-Methode der Schmetterlingsanimation auf dem Geometrischen Sketchpad
Artikeleinführung:1. Materialien vorbereiten: halbes Schmetterlingsbild, vorzugsweise im PNG- oder GIF-Format mit transparentem Hintergrund. 2. Verwenden Sie einen Kreis, um ein Parallelogramm zu konstruieren. ① Öffnen Sie die Software zum Zeichnen mathematischer Geometrie im geometrischen Skizzenblock und zeichnen Sie mit dem Kreiswerkzeug einen Kreis O. OA ist sein Radius. ② Markieren Sie Punkt O als Rotationszentrum. Drehen Sie Punkt A um 90° um Punkt O, um Punkt B zu erhalten. Wählen Sie einen beliebigen Punkt C auf dem Kreis zwischen A und B und wählen Sie ⊙O, Punkt C und Punkt B aus, um ihn zu konstruieren Bogen CB. ③ Konstruieren Sie Punkt D auf dem Bogen CB und erstellen Sie eine Animationsschaltfläche für Punkt D auf dem Bogen CB. ④ Markieren Sie den Vektor OD und verschieben Sie den Punkt A nach E entsprechend, um das Parallelogramm OAED zu erhalten. 3. Ziehen Sie das vorbereitete halbe Schmetterlingsbild auf das geometrische Zeichenbrett, wählen Sie es aus und kopieren Sie es. 4. Wählen Sie nacheinander die drei Punkte D, O und E aus und führen Sie [Bearbeiten] → [Einfügen] aus.
2024-04-17
Kommentar 0
972
So erstellen Sie eine Schmetterlingsanimation mit einem geometrischen Skizzenblock
Artikeleinführung:1. Bereiten Sie Materialien vor: halbes Schmetterlingsbild, vorzugsweise im PNG- oder GIF-Format mit transparentem Hintergrund. 2. Verwenden Sie einen Kreis, um ein Parallelogramm zu erstellen. ① Öffnen Sie die Software zum Zeichnen von geometrischen Skizzen und mathematischen Geometrien und verwenden Sie das Kreiswerkzeug „Zeichnen“. ein Kreis O, OA ist sein Radius. ② Markieren Sie Punkt O als Rotationszentrum. Drehen Sie Punkt A um 90° um Punkt O, um Punkt B zu erhalten. Wählen Sie einen beliebigen Punkt C auf dem Kreis zwischen A und B und wählen Sie ⊙O, Punkt C und Punkt B aus, um ihn zu konstruieren Bogen CB. ③ Konstruieren Sie Punkt D auf dem Bogen CB und erstellen Sie eine Animationsschaltfläche für Punkt D auf dem Bogen CB. ④ Markieren Sie den Vektor OD und verschieben Sie den Punkt A nach E entsprechend, um das Parallelogramm OAED zu erhalten. 3. Ziehen Sie das vorbereitete halbe Schmetterlingsbild auf das geometrische Zeichenbrett, wählen Sie es aus und kopieren Sie es. 4. Wählen Sie nacheinander D und O aus
2024-04-17
Kommentar 0
694

Eine grafische Methode zum Zeichnen eines Dreiecks mit bekannten drei Seitenlängen mithilfe eines geometrischen Skizzenblocks
Artikeleinführung:Beispielsweise ist bekannt, dass die Längen der drei Seiten eines Dreiecks 3, 4 und 5 betragen. Die spezifischen Vorgänge lauten wie folgt: 1. Öffnen Sie den Geometrie-Skizzenblock, führen Sie [Daten] - [Neuer Parameter] aus und erstellen Sie einen neuer Parameter a=3; b=4; c=5, Einheit Wählen Sie [Abstand], wählen Sie Parameter a und führen Sie [Transformieren] – [Abstand markieren] aus. 2. Zeichnen Sie mit dem [Punktwerkzeug] einen Punkt und wählen Sie ihn aus, führen Sie [Transformieren] - [Übersetzung] aus, setzen Sie den Winkel auf 0 und erhalten Sie einen weiteren Punkt. 3. Wählen Sie die beiden oben genannten Punkte aus und führen Sie den Befehl [Konstruktion]-[Liniensegment] aus, um ein Liniensegment zu konstruieren und ein Liniensegment mit einer festen Länge von 3 zu erhalten. 4. Wählen Sie einen Endpunkt des Liniensegments mit einer Länge von 3 und Parameter b aus, führen Sie [Konstruktion] - [Kreis mit Mittelpunkt und Radius zeichnen] aus, um einen Kreis zu zeichnen, und wählen Sie dann den anderen Endpunkt des Liniensegments und Parameter c aus. Ausführen [Konstruktion] – [Zeichne einen Kreis mit Mittelpunkt und Radius] Zeichne einen Kreis mit Mittelpunkt und Radius】Zeichne einen Kreis
2024-04-17
Kommentar 0
1257

So fügen Sie das Pfeilwerkzeug zum benutzerdefinierten Werkzeug von Geometric Sketchpad hinzu
Artikeleinführung:1. Konstruieren Sie Liniensegmente und Punkte. Zeichnen Sie ein Liniensegment AB in der Ebene, wählen Sie Punkt B aus und verschieben Sie ihn 1 cm nach oben, um Punkt C zu erhalten. 2. Konstruieren Sie Kreise und Schnittpunkte. Zeichnen Sie einen Kreis mit B als Mittelpunkt und C als Radius. Wählen Sie im Menü [Konstruktion] die Option [Kreis aus Mittelpunkt und Punkten auf dem Umfang konstruieren] und der Kreis schneidet das Liniensegment AB am Punkt D. 3. Konstruieren Sie den Symmetriepunkt des Schnittpunkts. Doppelklicken Sie auf Punkt B, wählen Sie Punkt D aus, wählen Sie [Drehen] unter [Transformieren] und stellen Sie den Drehwinkel auf 180 Grad ein, um Punkt D‘ zu konstruieren. 4. Drehen Sie Punkt B und konstruieren Sie einen Symmetriepunkt des Rotationspunkts. Doppelklicken Sie auf Punkt D‘, wählen Sie Punkt B aus, wählen Sie im Menü [Transformieren] die Option [Drehen], stellen Sie den Drehwinkel auf 15 Grad ein und erhalten Sie Punkt E. Doppelklicken Sie auf das Liniensegment AB und wählen Sie im Menü [Transformieren] die Option [Spiegelung], um Punkt F zu erhalten. 5. Wählen Sie die Punkte E, F und D’ aus, um ein Dreieck zu konstruieren
2024-04-22
Kommentar 0
1097

Detaillierte Vorgehensweise zur Verwendung des n-Gleichwinkel-Werkzeugs zum Halbieren eines Kreises auf dem geometrischen Skizzenblock
Artikeleinführung:Schritt 1: Zeichnen Sie einen Kreis. Öffnen Sie den geometrischen Skizzenblock, klicken Sie auf das [Kreis-Werkzeug] in der Seitenleiste und erstellen Sie einen Kreis auf der Leinwand. Schritt 2: Erstellen Sie einen neuen Parameter. Wenn Sie den Kreis in 20 gleiche Teile teilen möchten, klicken Sie zunächst in der Menüleiste auf [Daten] – Neuer Parameter, geben Sie 10 in das Popup-Dialogfeld ein und klicken Sie dann auf [OK]. Taste. Sie können sehen, dass die Parameter in der oberen linken Ecke der Leinwand erstellt wurden. Schritt 3: Klicken Sie in der Seitenleiste auf das [Liniensegment-Lineal-Werkzeug], um den Kreis zu halbieren, zeichnen Sie einen Durchmesser des Kreises und beschriften Sie den Mittelpunkt des Kreises und die beiden Endpunkte des Durchmessers [O, A, B]. Klicken Sie in der linken Seitenleiste auf [Werkzeuge anpassen] – Winkelwerkzeug – n Halbierungswinkelwerkzeug. Klicken Sie mit der Maus nacheinander auf Punkt A, Punkt O und Punkt B und klicken Sie dann auf den neu erstellten Parameter. Sie können sehen, dass die Hälfte des Kreises in 10 gleiche Teile unterteilt ist. Klicken Sie auf Punkt B, Punkt O und
2024-04-17
Kommentar 0
561
Wie man einen geometrischen Pythagoras-Baum auf einem Zeichenbrett herstellt
Artikeleinführung:1. Zeichnen Sie mit der Rotationsmethode das Quadrat ABCD (1) und das Liniensegment AB. (2) Doppelklicken Sie auf Punkt A, um Punkt A als Drehzentrum zu markieren. Wählen Sie Punkt B aus, wählen Sie den Befehl [Transformieren]-[Drehen] und drehen Sie Punkt B um 90 Grad, um Punkt D zu erhalten. (3) Doppelklicken Sie auf Punkt D, um Punkt D als Drehzentrum zu markieren. Wählen Sie Punkt A aus, wählen Sie den Befehl [Transformieren]-[Drehen] und drehen Sie Punkt A um -90 Grad, um Punkt C zu erhalten. (4) Zeichnen Sie die Liniensegmente AD, DC und BC. 2. Konstruieren Sie den Mittelpunkt E von DC und konstruieren Sie einen Kreis mit Punkt E als Mittelpunkt und EC als Radius. (1) Wählen Sie das Liniensegment DC aus, wählen Sie den Befehl [Konstruieren]-[Mittelpunkt] und zeichnen Sie den Mittelpunkt E von Gleichstrom. (2) Wählen Sie nacheinander Punkt E und Punkt C aus und wählen Sie den Befehl [Konstruktion] – [Zeichnen Sie einen Kreis mit dem Mittelpunkt des Kreises und Punkten auf dem Umfang]. 3. Struktur
2024-04-08
Kommentar 0
904

So zeichnen Sie geometrische Figuren nach bekannten Bedingungen im geometrischen Skizzenblock
Artikeleinführung:Beispielsweise ist bekannt, dass im Trapez ABCD AD∥BC, AB=AD+BC gilt und E der Mittelpunkt von CD ist. Beweisen Sie: AE und BE halbieren ∠BAD bzw. ∠ABC. Wir können von den bekannten Bedingungen ausgehen und die folgenden Schritte befolgen, um eine Figur zu zeichnen, die der Bedeutung der Frage auf dem geometrischen Skizzenblock entspricht. Öffnen Sie den geometrischen Skizzenblock, zeichnen Sie mit dem [Punkt-Werkzeug] zwei Punkte A und B in den leeren Bereich des Skizzenblocks, wählen Sie das [Strahlen-Werkzeug] aus, um horizontale Strahlen durch die Punkte A bzw. B zu zeichnen, und wählen Sie die Punkte A und B aus Konstruieren Sie Liniensegmente. Wählen Sie mit dem [Punktwerkzeug] einen beliebigen Punkt F auf dem Liniensegment AB aus, nehmen Sie die Punkte A und B als Mittelpunkte und verwenden Sie die Längen von AF und BF als Radien, um Kreise zu zeichnen. Die Strahlen mit den beiden Basen schneiden sich Punkte D und C. Offensichtlich ist AD+BC =AB. Nehmen Sie den Mittelpunkt E des Liniensegments CD und verbinden Sie AE und BE. ausgewählten Punkt
2024-04-17
Kommentar 0
479

Das neue Meta Avatar SDK bietet den Bewohnern des Metaverses mehr Begehbarkeit
Artikeleinführung:IT House berichtete am 24. Dezember, dass die mit Spannung erwartete MetaAvatars SDK24-Version endlich Beinfunktionen hinzufügte und es den Bewohnern des Metaversums ermöglichte, sich vom schwebenden Zustand zu verabschieden und offiziell in die bodenständige virtuelle Welt einzutreten Lediglich der komische Oberkörper wurde in den sozialen Medien und der Tech-Welt lächerlich gemacht. Während Meta im August bzw. September Beine zum Quest-Hauptmenü und zu den Plattformidentitäten von Horizon Worlds hinzufügte, war das öffentliche MetaAvatars SDK für Drittanbieter-Apps wie GOLF+ und Eleven Table Tennis bis jetzt, fast sechs Monate später, ohne Beine, MetaAvatarsSD
2024-01-03
Kommentar 0
1039
Was sind die am häufigsten verwendeten Tastenkombinationen für 2D-Grafiken in CAD-Software?
Artikeleinführung:Was sind die am häufigsten verwendeten Tastenkombinationen für CAD2-Maßzeichnungen? L Linie A Bogen I Block einfügen B Block erstellen H Musterfüllung D Bemaßungsstil-Manager E Löschen F Verrundung G Gruppe M Verschieben O Versatz P Verschieben S Strecken X Explodieren Z Maßstab anzeigen T mehrzeilig Text co kopieren MI spiegeln AR Array RO drehen SC skalieren EX strecken TR trimmen ST Textstil-Manager Abfrageabstand AA Bereich MA Merkmalsübereinstimmung LS Listenanzeige LA Ebenenbeschriftung DAL Ausrichtungsbeschriftung DCO fortlaufende Beschriftung DRA Radiusbeschriftung F3: Steuern Sie, ob die automatische Objektfangfunktion realisiert werden soll F7: Steuerung des Rasteranzeigemodus. F8: Steuerung des Orthogonalmodus. Strg+C
2024-01-05
Kommentar 0
1559

Verbesserte Beinfunktionalität und Grafik: Meta Avatars SDK 24 bringt neue Änderungen für den schwebenden Zustand
Artikeleinführung:Laut Nachrichten vom 24. Dezember hat das Meta-Unternehmen kürzlich die mit Spannung erwartete Version metaAvatarsSDK24 veröffentlicht. Dieses Update führt die lange fehlende Beinfunktion ein, die es den Bewohnern des Metaversums ermöglicht, mit einem vollständigeren Bild in der virtuellen Umgebung zu erscheinen. Dieses Update bedeutet, dass der Avatar des Benutzers kein schwebendes Bild in halber Länge mehr sein wird, sondern vollständig stehen und sich bewegen kann. Dies ist ein wichtiger Schritt für Meta bei der Schaffung einer realistischeren und immersiveren virtuellen Welt. Zuvor war Metas Virtual-Reality-Avatar Gegenstand von Witzen in den sozialen Medien und der Tech-Community, weil er nur aus seinem Oberkörper bestand. meta im August und September letzten Jahres trotz der Erweiterung des Quest-Hauptmenüs und der Inkarnation der HorizonWorlds-Plattform.
2024-01-08
Kommentar 0
933











