

Herausgeber |. Ziluo
Tiefes maschinelles Lernen hat in verschiedenen Bereichen der KI bemerkenswerte Erfolge erzielt, aber das gleichzeitige Erreichen einer hohen Interpretierbarkeit und hohen Effizienz ist immer noch eine ernsthafte Herausforderung
Tensor-Netzwerk, nämlich Tensor Network (TN), stammt aus der Quantenmechanik und ist ein ausgereiftes mathematisches Werkzeug. Es hat einzigartige Vorteile bei der Entwicklung effizienter „White-Box“-Lösungen für maschinelles Lernen gezeigt
Kürzlich ließen sich Ran Shiju von der Capital Normal University und Su Gang von der University of Chinese Academy of Sciences von der Quantenmechanik inspirieren und überprüften eine TN-basierte Innovationsmethode. Bereitstellung einer vielversprechenden Lösung für die seit langem bestehende Herausforderung, Interpretierbarkeit und Effizienz beim tiefen maschinellen Lernen in Einklang zu bringen.
Einerseits kann die Interpretierbarkeit von TN ML durch eine solide theoretische Grundlage basierend auf Quanteninformation und Vielteilchenphysik erreicht werden. Andererseits können leistungsstarke TN-Ausdrücke und fortschrittliche Rechentechniken, die in der Quanten-Vielteilchenphysik entwickelt wurden, eine hohe Effizienz erzielen. Mit der rasanten Entwicklung von Quantencomputern wird erwartet, dass TN in naher Zukunft neuartige Lösungen hervorbringen wird, die auf Quantenhardware in Richtung „Quanten-KI“ laufen können
Diese Rezension basiert auf „Tensor-Netzwerke für interpretierbare und effiziente Inspired Machine Learning “ trug den Titel „Intelligent Computing“ und wurde am 17. November 2023 veröffentlicht.

Link zum Papier: https://spj.science.org/doi/10.34133/icomputing.0061
Deep-Learning-Modelle, insbesondere neuronale Netzwerkmodelle, werden aufgrund ihrer Entscheidung oft als „Black Boxes“ bezeichnet Der Herstellungsprozess ist komplex und schwer zu erklären. Neuronale Netze sind derzeit das leistungsstärkste Deep-Learning-Modell. Ein Paradebeispiel für seine Leistungsfähigkeit ist GPT. Aufgrund der mangelnden Erklärbarkeit stehen jedoch auch GPT vor ernsthaften Problemen wie Robustheit und Datenschutz. Die mangelnde Erklärbarkeit dieser Modelle kann zu einem Mangel an Vertrauen in ihre Vorhersagen und Entscheidungen führen und somit ihre Verwendung in wichtigen praktischen Bereichen einschränken Anwendung
Tensornetzwerke basierend auf Quanteninformation und Mehrkörperphysik bieten einen „White-Box“-Ansatz für ML. Die Forscher sagten: „Tensornetzwerke spielen eine entscheidende Rolle bei der Verbindung von Quantenkonzepten, -theorien und -methoden mit ML und der effektiven Implementierung von auf Tensornetzwerken basierendem ML.“ Die Quantenphysik hat leistungsstarke „White-Box“-Mathematikwerkzeuge hervorgebracht.
Mit der rasanten Entwicklung des klassischen und Quantencomputings liefert TN neue Ideen zur Überwindung des Dilemmas zwischen Interpretierbarkeit und Effizienz. TN ist definiert als die Kontraktion mehrerer Tensoren. Seine Netzwerkstruktur bestimmt, wie der Tensor schrumpft.In Abbildung 1 ist eine schematische Darstellung der drei TN-Typen dargestellt. Diese drei Typen sind die Matrixproduktzustandsdarstellung (MPS), die Baum-TN und die projizierte verschränkte Paarzustandsdarstellung (PEPS)
Abbildung 1: Grafische Darstellung von 3 TN-Typen: (A) MPS, (B) )Baum-TN und (C)PEPS. (Quelle: Papier)
TN hat auf dem Gebiet der Quantenmechanik bemerkenswerte Erfolge als effiziente Darstellung des Zustands großer Quantensysteme erzielt. In der TN-Theorie können Zustände, die das Flächengesetz der Verschränkungsentropie erfüllen, effizient durch eine TN-Darstellung mit endlichen Bindungsdimensionen angenähert werden. 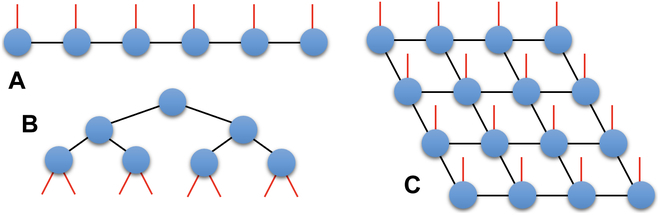
Bild 2: MPS ( Tensor-Train-Form) kann verwendet werden, um eine große Anzahl mathematischer Objekte effektiv darzustellen oder zu formulieren. (Zitiert aus: Aufsatz)
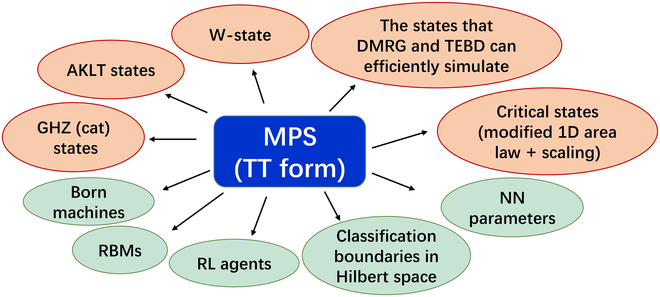 Technologische Fortschritte beim maschinellen Lernen, inspiriert durch Quanten (Technologische Fortschritte beim maschinellen Lernen, inspiriert durch Quanten)
Technologische Fortschritte beim maschinellen Lernen, inspiriert durch Quanten (Technologische Fortschritte beim maschinellen Lernen, inspiriert durch Quanten)
TN bietet dank seiner fundierten Theorie und effektiven Methoden eine neue Möglichkeit, das Dilemma zwischen Interpretierbarkeit und Effizienz beim maschinellen Lernen zu lösen. Derzeit werden zwei miteinander verflochtene Forschungsrichtungen diskutiert:
In diesem Inhalt stellen Forscher die jüngsten ermutigenden Fortschritte bei quanteninspiriertem ML aus der Perspektive von Feature-Mapping, Modellierung und quantencomputerbasiertem ML vor und eröffnen Diskussionen rund um diese beiden Themen. Diese Fortschritte stehen in engem Zusammenhang mit den Vorteilen des Einsatzes von TN bei der Verbesserung der Effizienz und Interpretierbarkeit. Diese ML-Ansätze werden oft als „quanteninspiriert“ bezeichnet, da ihre Theorien, Modelle und Methoden aus der Quantenphysik stammen oder von dieser inspiriert sind. Wir brauchen jedoch mehr Anstrengungen, um ein Systemgerüst für Interpretierbarkeit auf der Grundlage der Quantenphysik zu entwickeln.
In der folgenden Tabelle sind die wichtigsten Methoden zu TN ML und ihre Beziehung zu Effizienz und Interpretierbarkeit zusammengefasst Maschinelles Lernen
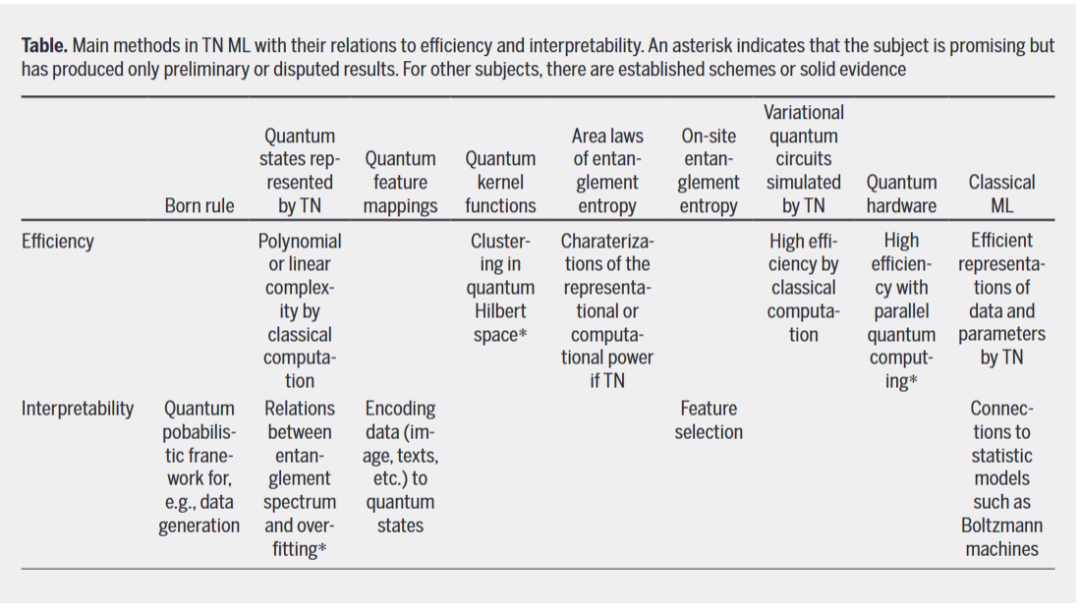 Als grundlegendes mathematisches Werkzeug sind die Anwendungen neuronaler Netze in ML nicht auf solche beschränkt, die quantenprobabilistischen Interpretationen folgen. Da TN zur effektiven Darstellung und Simulation der Partitionsfunktion klassischer stochastischer Systeme wie der Ising- und Potts-Modelle verwendet werden kann, wurde die Beziehung zwischen TN und Boltzmann-Maschinen ausführlich untersucht.
Als grundlegendes mathematisches Werkzeug sind die Anwendungen neuronaler Netze in ML nicht auf solche beschränkt, die quantenprobabilistischen Interpretationen folgen. Da TN zur effektiven Darstellung und Simulation der Partitionsfunktion klassischer stochastischer Systeme wie der Ising- und Potts-Modelle verwendet werden kann, wurde die Beziehung zwischen TN und Boltzmann-Maschinen ausführlich untersucht.
TN wird auch verwendet, um NN zu verbessern und neuartige ML-Modelle zu entwickeln, wobei jegliche probabilistische Interpretation ignoriert wird. Ins Chinesische umgeschrieben: TN wird auch verwendet, um NN zu verbessern und neuartige ML-Modelle zu entwickeln, unabhängig von einer probabilistischen Interpretation. Auf derselben Grundlage werden Modellkomprimierungsmethoden vorgeschlagen, um die Variationsparameter von NN in TN zu zerlegen oder die Variationsparameter direkt als TN darzustellen. Letzteres erfordert möglicherweise keinen expliziten Zerlegungsprozess, bei dem die Parameter des neuronalen Netzwerks nicht in Tensoren, sondern direkt in TT-Formen, Matrixproduktoperatoren oder tiefen TNs wiederhergestellt werden. TN wurden nichtlineare Aktivierungsfunktionen hinzugefügt, um die ML-Leistung zu verbessern und TN von multilinearen Modellen auf nichtlineare Modelle zu verallgemeinern.
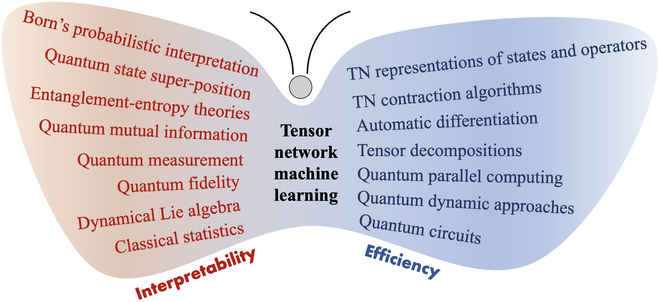
Was neu geschrieben werden muss, ist: FazitDie Menschen sind seit langem daran interessiert, das Dilemma zwischen Effizienz und Erklärbarkeit in der künstlichen Intelligenz (insbesondere tiefem maschinellen Lernen) zu lösen. In diesem Zusammenhang überprüfen wir die ermutigenden Fortschritte von TN, einer interpretierbaren und effizienten quanteninspirierten Methode des maschinellen Lernens. Der „N ML-Schmetterling“ in Abbildung 3 listet die Erfolge von TN im Bereich ML Advantage auf. Für quanteninspiriertes ML lassen sich die Vorteile von TN in zwei Schlüsselaspekten zusammenfassen: Quantentheorie für Interpretierbarkeit und Quantenmethoden für verbesserte Effizienz. Einerseits ermöglicht uns TN, Statistiken und Quantentheorie (z. B. Verschränkungstheorie) anzuwenden, um probabilistische Rahmenwerke für die Interpretierbarkeit zu erstellen, die möglicherweise über das hinausgehen, was durch klassische Information oder statistische Theorie beschrieben werden kann. Andererseits werden leistungsstarke quantenmechanische TN-Algorithmen und eine stark verbesserte Quantencomputertechnologie dazu führen, dass quanteninspirierte TN-ML-Methoden sowohl auf klassischen als auch auf Quantencomputerplattformen hocheffizient sind.
Abbildung 3: „TN ML Butterfly“ fasst zwei einzigartige Vorteile zusammen: Interpretierbarkeit basierend auf Quantentheorie (linker Flügel) und Effizienz basierend auf Quantenmethoden (rechter Flügel). (Quelle: Papier) Insbesondere mit den jüngsten erheblichen Fortschritten im Bereich GPT kam es zu einem beispiellosen Anstieg der Modellkomplexität und Rechenleistung, der TN ML neue Chancen und Herausforderungen mit sich brachte. Angesichts der aufkommenden GPT-KI wird Erklärbarkeit immer wertvoller, nicht nur um die Forschungseffizienz zu verbessern, sondern auch um eine bessere Anwendung und sicherere Kontrolle zu ermöglichenIn der aktuellen NISQ-Ära und der kommenden realen Ära des Quantencomputers entwickelt sich TN schnell entwickelt sich zu einem wichtigen mathematischen Werkzeug zur Erforschung der künstlichen Quantenintelligenz aus verschiedenen Perspektiven wie Theorie, Modell, Algorithmus, Software, Hardware und Anwendung
 Referenzinhalt:
Referenzinhalt:
Das obige ist der detaillierte Inhalt vonZusammenfassung der Zusammenarbeit zwischen der National University of Science and Technology und der First Normal University: Aufdecken, wie „White-Box'-Tensornetzwerke die Interpretierbarkeit und Effizienz des quantenmaschinellen Lernens verbessern können. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




