Zunächst müssen wir noch erklären, dass der Hauptinhalt, den wir studieren, Binärbäume sind, da Binärbäume die typischste Anwendung von Bäumen sind, die man kennen und lernen muss Inhalt.
Bevor wir die Funktionsweise des Baums lernen, müssen wir zunächst verstehen, dass der Kern der Funktionsweise des Baums das „Durchqueren“ ist. Warum sagst du das? Im Gegensatz zu Stapeln und Warteschlangen ist die Baumstruktur tatsächlich nicht mehr eindimensional. Sie hat Zweige, verschiedene Winkel und, was noch wichtiger ist, das Konzept der Hierarchie.
Dinge im eindimensionalen Raum sind unsere gemeinsamen „Linien“, die nur Länge, aber keine Höhe haben, und diese Länge ist ihre einzige Dimension. Stapel und Warteschlangen sind offensichtlich eindimensional. Aufgrund des hierarchischen Konzepts hat der Baum eine „Höhe“, das heißt, er wurde zu einem zweidimensionalen Konzept aufgewertet. Genau wie bei der Reihe von Substantiven, die im vorherigen Artikel vorgestellt wurden, gibt es das Konzept der „Höhe (Tiefe) eines Baumes“.
Nachdem wir einen Baum durchlaufen haben, können wir den Knoten des Baums basierend auf dem Durchlauf hinzufügen, löschen, ändern und andere Operationen durchführen. Beginnen ihre logischen Operationen nicht auch mit der Durchquerung? Egal, ob es sich um das Knallen oder Betreten des Stapels oder das Aus- oder Einreihen in die Warteschlange handelt, wir alle basieren auf einer festen Durchlaufregel (FILO, FIFO).
Bei zweidimensionalen Dingen ist die Art und Weise, wie man sie durchquert, ein entscheidender Punkt. Wir müssen die eindimensionale Datenstruktur nur sequentiell durchlaufen, aber die zweidimensionalen Datenergebnisse können nicht einfach einzeln der Reihe nach durchlaufen werden, da es hierarchische Beziehungen zwischen Knoten gibt, sodass wir die aktuelle Situation berücksichtigen müssen. Wenn der Knoten keine hat Untergeordnete Knoten, was sollen wir mit unserer Durchquerungsoperation machen?
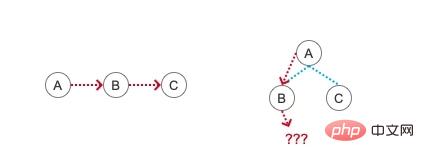
Glücklicherweise lernen wir dieses Wissen, indem wir auf den Schultern von Riesen stehen. Viele Senioren haben für uns einige sehr einfache Baumdurchquerungsmethoden zusammengefasst. Wie einfach sind sie? Lassen Sie uns zunächst aus dem Weg gehen und einen Blick darauf werfen, wie man einen Baum erstellt. Dabei handelt es sich um den Binärbaum, den wir im vorherigen Artikel gezeigt haben.
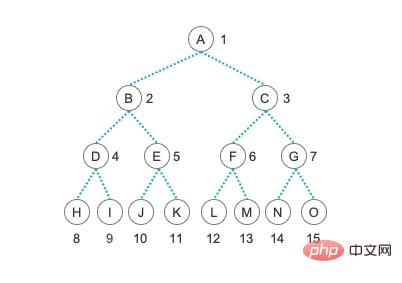
Die Verwendung von verkettetem Speicher zum Speichern von Binärbäumen ist sehr einfach und sehr anschaulich. Freunde, legen Sie bitte Ihre Fragen zur sequentiellen Speicherung von Binärbäumen beiseite, denn wir werden sie im nächsten Artikel erklären Wann sollte sequentieller Speicher verwendet werden?
class BiTree
{
public $data;
public $lChild;
public $rChild;
}Tatsächlich verwenden wir bei der Kettenspeicherung Knoten nacheinander, um den Baum zu speichern. Jeder Binärbaumknoten verfügt über ein Datenfeld, das Datenattribut. Die anderen beiden Attribute können als zwei gegabelte Zeiger betrachtet werden, nämlich der linke untergeordnete Knoten lChild und der rechte untergeordnete Knoten rChild dieses Knotens.
Beim Vergleich des Stapels und der Warteschlange haben wir lediglich den nächsten Knoten durch den linken und rechten untergeordneten Knoten ersetzt. Im Wesentlichen unterscheidet er sich nicht wesentlich vom Stapel und der Warteschlange. Um es ganz klar auszudrücken: Aus Sicht der Datenstruktur verwenden wir immer noch eindimensionale Speicherung, um zweidimensionale Konzepte darzustellen, und die Transformation dieses Konzepts erfordert, dass wir aus der Perspektive des konzeptionellen Verständnisses beginnen.
// 建立二叉树
function CreateBiTree($arr, $i)
{
if (!isset($arr[$i])) {
return null;
}
$t = new BiTree();
$t->data = $arr[$i];
$t->lChild = CreateBiTree($arr, $i * 2);
$t->rChild = CreateBiTree($arr, $i * 2 + 1);
return $t;
}Mit einer so einfachen Methode können wir die Erstellung eines verketteten Binärbaums abschließen. Freunde, bitte schauen Sie genau hin, dieser einfache Vorgang zum Erstellen eines Baums birgt tatsächlich viele Geheimnisse:
Wir verwenden ein Array, um jeden Knoten des Baums der Reihe nach darzustellen, z. B. die Eingabe von A, B, C, D, E nacheinander ... (Wir werden sie in der sequentiellen Speicherung des Baums wieder sehen)
Der zugewiesene Inhalt sind die Daten des aktuellen $i-Index. Beachten Sie, dass wir beim Zuweisen von Werten nach links und rechts eine rekursive Operation durchgeführt haben Richtige Kinder
Beim Erlernen des Stapels haben wir gelernt, dass „Rekursion“ eine Stapeloperation ist. Daher erstellen wir in diesem Code den Baum in Form eines Stapels. Beachten Sie, dass jedes Mal, wenn ich 2 und ich 2 + 1, oder? Bitte überprüfen Sie Eigenschaft 5 von Binärbäumen
Abschließend testen wir, ob diese Methode erfolgreich eine verknüpfte Baumstruktur aufbauen kann.
$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O']; $tree = CreateBiTree($treeList, 1); print_r($tree); // BiTree Object // ( // [data] => A // [lChild] => BiTree Object // ( // [data] => B // [lChild] => BiTree Object // ( // [data] => D // [lChild] => BiTree Object // ( // [data] => H // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => I // [lChild] => // [rChild] => // ) // ) // [rChild] => BiTree Object // ( // [data] => E // [lChild] => BiTree Object // ( // [data] => J // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => K // [lChild] => // [rChild] => // ) // ) // ) // [rChild] => BiTree Object // ( // [data] => C // [lChild] => BiTree Object // ( // [data] => F // [lChild] => BiTree Object // ( // [data] => L // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => M // [lChild] => // [rChild] => // ) // ) // [rChild] => BiTree Object // ( // [data] => G // [lChild] => BiTree Object // ( // [data] => N // [lChild] => // [rChild] => // ) // [rChild] => BiTree Object // ( // [data] => O // [lChild] => // [rChild] => // ) // ) // ) // )
说完二叉树的建树了，其实我们就已经接触到了一种二叉树的遍历形式。注意看我们建树方法中的代码，我们是先给结点的 data 赋值，然后建立这个结点的左、右孩子结点，并为它们赋值后再继续使用同样的操作一路建立完成所有的结点。现在，我们将这个操作反过来，不是建立结点，而是读取这些结点的内容，先读取结点的内容，然后再读取这个结点左右孩子结点的内容，这就是“先序遍历”。
先序遍历
/**
* 前序遍历
*/
function PreOrderTraverse(?BiTree $t)
{
if ($t) {
echo $t->data, ',';
PreOrderTraverse($t->lChild);
PreOrderTraverse($t->rChild);
}
}
PreOrderTraverse($tree);
// A,B,D,H,I,E,J,K,C,F,L,M,G,N,O,是不是很神奇？就连建树我们竟然也使用的是同一种遍历的方法，可以看出对于二叉树这种复杂的数据结构来说，遍历的重要作用了吧。
大家可以看一个遍历读取出来的结点顺序，貌似和我们输入的顺序不一样呀！没错，先序遍历是通过递归，先按一个方向走到底，当这个结点没有子结点之后，通过递归栈的特性再向上弹出。并且在遍历孩子结点之前先输出当前这个结点的内容。注意，这一句话很重要！所以我们的顺序就是 A,B,D,H ，当 H 没有子结点之后，我们就回到父结点 D 再进入它的右子结点 I ，具体顺序可以参考下图：
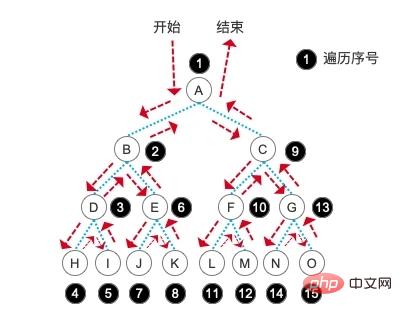
我们代码中的先序遍历和先序建树的结点顺序是完全不一样的，这一点也是要搞清楚的。建树的过程我们根据二叉树的 性质5 直接为它指定了数据下标。而在遍历过程中则是一个结点一个结点的去扫描遍历整颗树的。
中序遍历
顾名思义，中序遍历其实就是在遍历完左孩子结点之后再输出当前这个结点的内容，所以我们只需要微调先序遍历的代码即可。
/**
* 中序遍历
*/
function InOrderTraverse(?BiTree $t)
{
if ($t) {
InOrderTraverse($t->lChild);
echo $t->data, ',';
InOrderTraverse($t->rChild);
}
}
InOrderTraverse($tree);
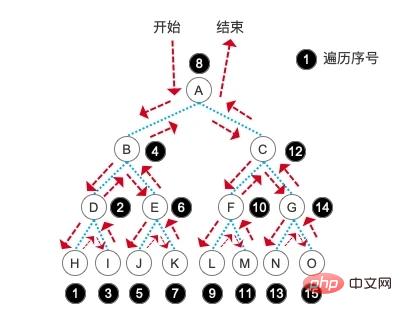
// H,D,I,B,J,E,K,A,L,F,M,C,N,G,O,中序遍历的步骤就是我们会直接先走到最左边的子结点，当遇到最后一个结点时，输出内容，也就是图中的 H 结点，接着回到它的父结点 D 结点，这时根据中序的原理输出 D ，再进入它的右孩子结点并输出 I 。
D 结点的子树及它本身遍历完成后，返回 D 结点的上级结点 B 结点，输出 B ，然后进入 B 结点的右孩子结点 E 。再次进入到 E 的最左孩子结点 J ，然后参考 D 结点的遍历形式完成整颗树的遍历。具体顺序参考下图：
后序遍历
在学习了先序和中序之后，从名字就可以看出来后序就是在遍历完一个结点的左右孩子之后最后输出这个结点的内容，代码当然也是简单地微调一下就可以了。
/**
* 后序遍历
*/
function PostOrderTraverse(?BiTree $t)
{
if ($t) {
PostOrderTraverse($t->lChild);
PostOrderTraverse($t->rChild);
echo $t->data, ',';
}
}
PostOrderTraverse($tree);
// H,I,D,J,K,E,B,L,M,F,N,O,G,C,A,具体原理就不详细说明了，相信在学习了先序和中序之后，你一定能马上想明白后序遍历到底是什么意思了。直接上图：
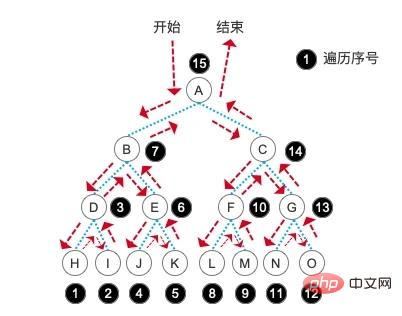
层序遍历
最后，我们要讲的就是层序遍历。既然有“层”这个关键字了，相信大家马上就能联想到，是不是一层一层地去遍历啊！没错，层序遍历就是这个意思，我们按照树的层次，一层一层地输出相应的结点信息。需要注意的，在这里我们会用到队列，而不是栈了。
/**
* 层序遍历
*/
$q = InitLinkQueue();
function LevelOrderTraverse(?BiTree $t)
{
global $q;
if (!$t) {
return;
}
EnLinkQueue($q, $t);
$node = $q;
while ($node) {
$node = DeLinkQueue($q);
if ($node->lChild) {
EnLinkQueue($q, $node->lChild);
}
if ($node->rChild) {
EnLinkQueue($q, $node->rChild);
}
echo $node->data, ',';
}
}
LevelOrderTraverse($tree);
// A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,InitLinkQueue() EnLinkQueue() 、 EnLinkQueue() 这些都是我们之前学习队列的时候所写的对于队列的逻辑操作方法。是不是很开心呀，之前的知识又用上了。层序遍历的核心思想就是运用队列的概念，遇到一个结点，就把这个结点入队，然后判断它是否有子结点，然后相继把子结点入队。
每遍历一个结点，就把队首的结点出队，这样就完成了按树的层次遍历的能力。文字说明还是太抽象，我们还是通过图片来展示这一过程：
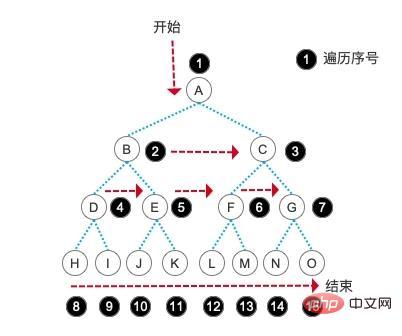
大家有没有发现，层序遍历的输出结果就和我们建树时的数组顺序完全相同了。很好玩吧，所以说代码的世界总是有无穷的乐趣等着我们去发现哦！
今天的内容有没有懵圈？如果懵圈了就多找资料好好研究一下，先序、中序、后序都是利用栈来进行树的结点遍历的，而层序遍历则是利用了队列。一环套一环呀，前面学习的内容都派上用场了吧！不过这只是个开始，在学习图的时候，我们会在深度遍历和广度遍历中再次看到栈和队列的身影，它们可都是亲戚哦。
这四种遍历方式在考试和面试中也是经常出现的，不管是它们的原理还是画图或者是根据图形来写出各种遍历的顺序，都是非常常见的考核内容，所以大家在这篇文章入门的基础上还是要更加深入的去根据一些教材来深入的理解这几种遍历，熟练的掌握它们。
测试代码：
https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/4.树/source/4.2二叉树的遍历及逻辑操作.php
推荐学习：php视频教程
Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung der Binärbaumdurchquerung und Methoden logischer Operationen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
So öffnen Sie eine PHP-Datei
So entfernen Sie die ersten paar Elemente eines Arrays in PHP
Was tun, wenn die PHP-Deserialisierung fehlschlägt?
So verbinden Sie PHP mit der MSSQL-Datenbank
So verbinden Sie PHP mit der MSSQL-Datenbank
So laden Sie HTML hoch
So lösen Sie verstümmelte Zeichen in PHP
So öffnen Sie PHP-Dateien auf einem Mobiltelefon
![[Web-Frontend] Node.js-Schnellstart](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
