Ändern Sie die Kantengewichte des Diagramms

2699. Kantengewichte des Diagramms ändern

Schwierigkeit:Schwer

Themen:Diagramm, Heap (Prioritätswarteschlange), kürzester Pfad

Sie erhalten einenungerichteten gewichteten zusammenhängendenGraphen mit n Knoten, die von 0 bis n - 1 beschriftet sind, und einem ganzzahligen Array von Kanten, wobei Kanten[i] = [a_i, b_i, w_i] zeigt an, dass es eine Kante zwischen den Knoten a_iund b_imit dem Gewicht w_i.

i_{= -1), während andere ein}positivesGewicht haben (wi_{> 0) .}

alle Kantenmit einer Gewichtung von -1 zu modifizieren, indem Sie ihnenpositive Ganzzahlwerteim Bereich [1, 2 * 109^{zuweisen ], sodass der}kürzeste Abstandzwischen den Knoten Quelle und Ziel einem ganzzahligen Ziel entspricht. Wenn esmehrere Änderungengibt, die dazu führen, dass die kürzeste Entfernung zwischen Quelle und Ziel dem Ziel entspricht, wird jede davon als korrekt angesehen.

ein Array zurück, das alle Kanten (auch unveränderte) in beliebiger Reihenfolge enthält, wenn es möglich ist, die kürzeste Entfernung von der Quelle zum Ziel gleich dem Ziel zu machen, oder einleeres Array, wenn dies unmöglich ist.

Hinweis:Sie dürfen die Gewichte von Kanten mit anfänglichen positiven Gewichten nicht ändern.

Beispiel 1:

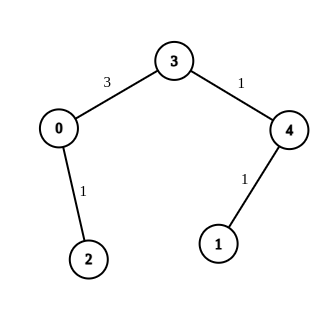
• Eingabe:n = 5, Kanten = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1] ], Quelle = 0, Ziel = 1, Ziel = 5
• Ausgabe:[[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
• Erklärung:Die obige Grafik zeigt eine mögliche Änderung an den Kanten, sodass der Abstand von 0 zu 1 gleich 5 ist.

Beispiel 2:

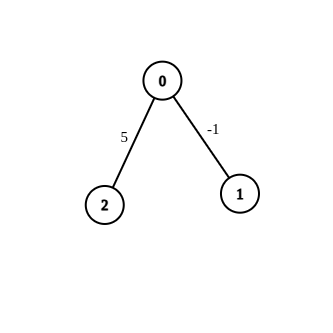
• Eingabe:n = 3, Kanten = [[0,1,-1],[0,2,5]], Quelle = 0, Ziel = 2, Ziel = 6
• Ausgabe:[]
• Erklärung:Die obige Grafik enthält die Anfangskanten. Es ist nicht möglich, den Abstand von 0 bis 2 auf 6 zu bringen, indem man die Kante mit der Gewichtung -1 ändert. Es wird also ein leeres Array zurückgegeben.

Beispiel 3:

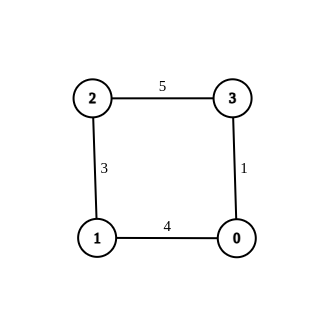
• Eingabe:n = 4, Kanten = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], Quelle = 0, Ziel = 2, Ziel = 6
• Ausgabe:[[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
• Erklärung:Die obige Grafik zeigt eine modifizierte Grafik mit dem kürzesten Abstand von 0 zu 2 als 6.

Einschränkungen:

1 <= n <= 100
1 <= Kanten.Länge <= n * (n - 1) / 2
edges[i].length == 3
0 <= a
• i_{, b}i_{< n}
w
• i_{= -1 oder 1 <= w}i_{<= 10}7
a
• i_{!= b}i
0 <= Quelle, Ziel < n
Quelle != Ziel
1 <= Ziel <= 10
• 9
Der Graph ist verbunden und es gibt keine Selbstschleifen oder wiederholte Kanten

Hinweis:

Überprüfen Sie zunächst, ob es tatsächlich möglich ist, den kürzesten Weg von der Quelle zum Ziel gleich dem Ziel zu machen.
Wenn der kürzeste Weg von der Quelle zum Ziel ohne die zu ändernden Kanten kürzer als das Ziel ist, ist dies nicht möglich.
Wenn der kürzeste Weg von der Quelle zum Ziel einschließlich der zu ändernden Kanten und der Zuweisung einer temporären Gewichtung von 1 größer als das Ziel ist, ist dies ebenfalls nicht möglich.
Angenommen, wir können eine modifizierbare Kante (u, v) finden, sodass die Länge des kürzesten Pfads von der Quelle zu u (dis1) plus die Länge des kürzesten Pfads von v zum Ziel (dis2) kleiner als das Ziel (dis1) ist + dis2 < Ziel), dann können wir seine Gewichtung in „Ziel – dis1 – dis2“ ändern.
Für alle anderen Kanten, die noch das Gewicht „-1“ haben, ändern Sie die Gewichte in ausreichend große Zahlen (Ziel, Ziel + 1 oder 200000000 usw.).

Lösung:

1. Erstkontrolle mit vorhandenen Gewichten:

   • Zuerst berechnen wir den kürzesten Weg von der Quelle zum Ziel, indem wir nur die Kanten mit positivem Gewicht verwenden und die Kanten mit dem Gewicht -1 ignorieren.
   • Wenn dieser Abstand bereits größer als das Ziel ist, ist es unmöglich, die -1-Kanten zu ändern, um das Ziel zu erreichen, daher geben wir ein leeres Array zurück.

2. Vorübergehende Gewichtszuweisung 1:

   • Als nächstes weisen Sie allen Kanten mit dem Gewicht -1 eine temporäre Gewichtung von 1 zu und berechnen den kürzesten Pfad neu.
   • Wenn dieser kürzeste Pfad immer noch größer als das Ziel ist, ist es unmöglich, das Ziel zu erreichen, also geben wir ein leeres Array zurück.

3. Bestimmte Kantengewichte ändern:

   • Durchlaufen Sie die Kanten mit der Gewichtung -1 und identifizieren Sie Kanten, die so angepasst werden können, dass sie genau der Zielentfernung entsprechen. Dies geschieht, indem das Gewicht einer Kante so angepasst wird, dass die kombinierten Entfernungen der Wege, die zu und von dieser Kante führen, die genaue Zielentfernung ergeben.
   • Für alle verbleibenden -1-Kanten weisen Sie eine Gewichtung zu, die groß genug ist (z. B. 2 * 10^9), um sicherzustellen, dass sie sich nicht auf den kürzesten Pfad auswirken.

4. Geänderte Kanten zurückgeben:

   • Zum Schluss wird die geänderte Liste der Kanten zurückgegeben.

Lassen Sie uns diese Lösung in PHP implementieren:2699. Kantengewichte des Diagramms ändern

        
Erläuterung:
        

         
Die Dijkstra-Funktion berechnet den kürzesten Weg von der Quelle zu allen anderen Knoten.
         
Wir berechnen zunächst den kürzesten Pfad und ignorieren -1-Kanten.
         
Wenn der Pfad ohne -1 Kanten kleiner als das Ziel ist, gibt die Funktion ein leeres Array zurück, was darauf hinweist, dass es unmöglich ist, die Gewichtungen anzupassen, um das Ziel zu erreichen.
         
Andernfalls setzen wir vorübergehend alle -1-Kanten auf 1 und prüfen, ob der kürzeste Weg das Ziel überschreitet.
         
Wenn dies der Fall ist, ist es erneut unmöglich, das Ziel zu erreichen, und wir geben ein leeres Array zurück.
         
Wir modifizieren dann die Gewichte der -1-Kanten strategisch, um den gewünschten kürzesten Weg mit genau dem Ziel zu erreichen.
        
Dieser Ansatz überprüft und passt die Kantengewichte effizient an und stellt so sicher, dass der Zielabstand nach Möglichkeit eingehalten wird.
Kontaktlinks
Wenn Sie diese Serie hilfreich fanden, denken Sie bitte darüber nach, demRepositoryeinen Stern auf GitHub zu geben oder den Beitrag in Ihren bevorzugten sozialen Netzwerken zu teilen? Ihre Unterstützung würde mir sehr viel bedeuten!
Wenn Sie weitere hilfreiche Inhalte wie diesen wünschen, folgen Sie mir gerne:
        

         
LinkedIn
         
GitHub
        
Das obige ist der detaillierte Inhalt vonÄndern Sie die Kantengewichte des Diagramms. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!