
2192. Alle Vorfahren eines Knotens in einem gerichteten azyklischen Graphen
Mittel
Sie erhalten eine positive ganze Zahl n, die die Anzahl der Knoten eines Gerichteten Azyklischen Graphen (DAG) darstellt. Die Knoten sind von 0 bis n - 1 (einschließlich) nummeriert.
Sie erhalten außerdem ein ganzzahliges 2D-Array mit Kanten, wobei Kanten[i] = [voni, bisi] angibt, dass es eine unidirektionale gibt Kante von voni bis zui im Diagramm.
Eine Listenantwort zurückgeben, wobei Antwort[i] die Liste der Vorfahren des iten Knotens ist, sortiert in aufsteigender Reihenfolge.
Ein Knoten u ist ein Vorfahre eines anderen Knotens v, wenn u über eine Reihe von Kanten v erreichen kann.
Beispiel 1:
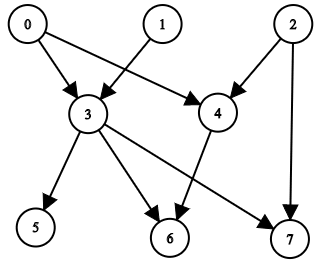
Beispiel 2:
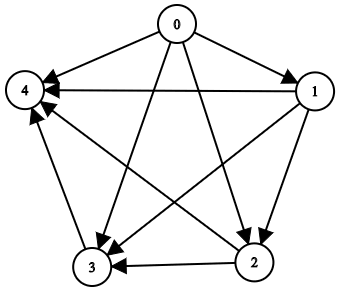
Einschränkungen:
Lösung:
class Solution {
/**
* @param Integer $n
* @param Integer[][] $edges
* @return Integer[][]
*/
function getAncestors($n, $edges) {
$adjacencyList = array_fill(0, $n, []);
foreach ($edges as $edge) {
$from = $edge[0];
$to = $edge[1];
$adjacencyList[$to][] = $from;
}
$ancestorsList = [];
for ($i = 0; $i < $n; $i++) {
$ancestors = [];
$visited = [];
$this->findChildren($i, $adjacencyList, $visited);
for ($node = 0; $node < $n; $node++) {
if ($node == $i) continue;
if (in_array($node, $visited))
$ancestors[] = $node;
}
$ancestorsList[] = $ancestors;
}
return $ancestorsList;
}
private function findChildren($currentNode, &$adjacencyList, &$visitedNodes) {
$visitedNodes[] = $currentNode;
foreach ($adjacencyList[$currentNode] as $neighbour) {
if (!in_array($neighbour, $visitedNodes)) {
$this->findChildren($neighbour, $adjacencyList, $visitedNodes);
}
}
}
}
Kontaktlinks
Das obige ist der detaillierte Inhalt vonAlle Vorfahren eines Knotens in einem gerichteten azyklischen Graphen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 So öffnen Sie eine VSD-Datei
So öffnen Sie eine VSD-Datei
 Methode zum Ändern des MySQL-Passworts
Methode zum Ändern des MySQL-Passworts
 Yiou Exchange-App herunterladen
Yiou Exchange-App herunterladen
 Detaillierte Erläuterung der Nginx-Konfiguration
Detaillierte Erläuterung der Nginx-Konfiguration
 So erstellen Sie eine Webseite in Python
So erstellen Sie eine Webseite in Python
 So lösen Sie das Problem, dass Apple nicht mehr als 200 Dateien herunterladen kann
So lösen Sie das Problem, dass Apple nicht mehr als 200 Dateien herunterladen kann
 So lösen Sie verstümmelte Filezilla-Zeichen
So lösen Sie verstümmelte Filezilla-Zeichen
 Welche Methoden gibt es zum Neustarten von Anwendungen in Android?
Welche Methoden gibt es zum Neustarten von Anwendungen in Android?




