当前,采用下一 token 预测范式的自回归大型语言模型已经风靡全球,同时互联网上的大量合成图像和视频也早已让我们见识到了扩散模型的强大之处。
近日,MIT CSAIL 的一个研究团队(一作为 MIT 在读博士陈博远)成功地将全序列扩散模型与下一 token 模型的强大能力统合到了一起,提出了一种训练和采样范式:Diffusion Forcing(DF)。
论文标题:Diffusion Forcing:Next-token Prediction Meets Full-Sequence Diffusion
论文地址:https://arxiv.org/pdf/2407.01392
项目网站:https://boyuan.space/diffusion-forcing
代码地址:https://github.com/buoyancy99/diffusion-forcing
如下所示,扩散强制在一致性和稳定性方面都明显胜过全序列扩散和教师强制这两种方法。

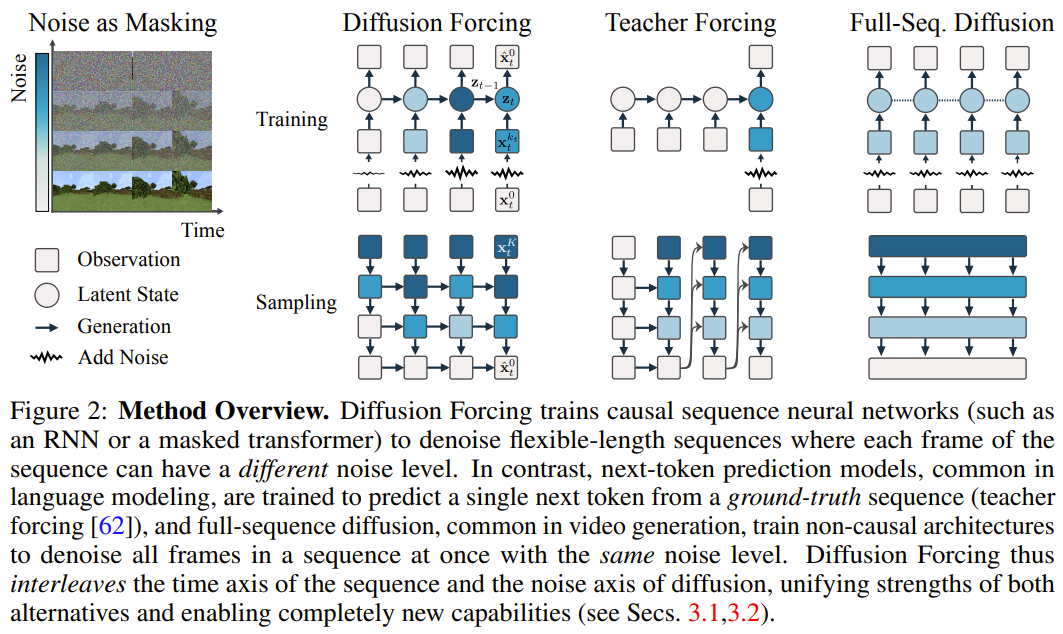
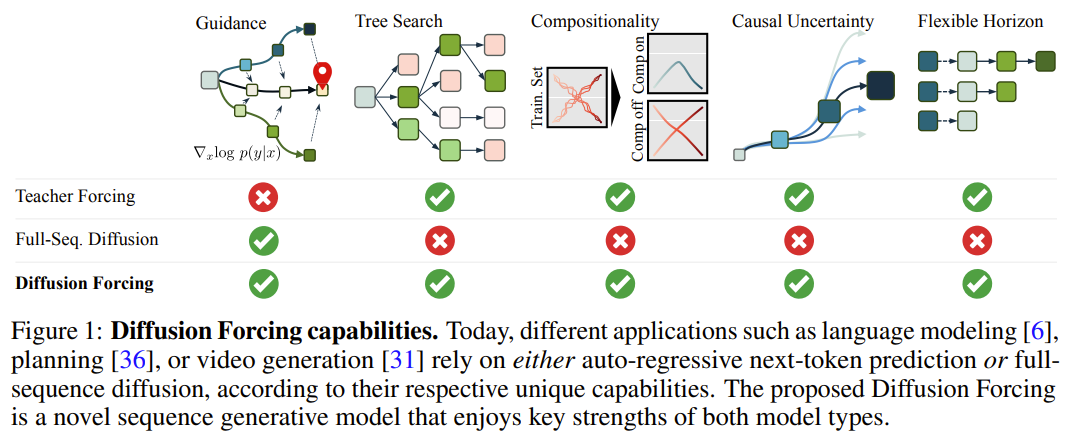
在该框架中,每个 token 都关联了一个随机的、独立的噪声水平,并且可使用一种共享的下一 token 预测模型或下几 token 预测模型根据任意的、独立的、每 token 的方案对 token 进行去噪。该方法的研究灵感来自这一观察:对 token 加噪声的过程就是一种形式的部分掩码过程 —— 零噪声就意味着未对 token 加掩码,而完整噪声则是完全掩蔽 token。因此,DF 可强迫模型学习去除任何可变有噪声 token 集合的掩码(图 2)。与此同时,通过将预测方法参数化为多个下一 token 预测模型的组合,该系统可以灵活地生成不同长度的序列,并以组合方式泛化到新的轨迹(图 1)。该团队将用于序列生成的 DF 实现成了因果扩散强制(Causal Diffusion Forcing/CDF),其中未来 token 通过一个因果架构依赖于过去 token。他们训练该模型一次性去噪序列的所有 token(其中每个 token 都有独立的噪声水平)。在采样期间,CDF 会将一个高斯噪声帧序列逐渐地去噪成洁净的样本,其中不同帧在每个去噪步骤可能会有不同的噪声水平。类似于下一 token 预测模型,CDF 可以生成长度可变的序列;不同于下一 token 预测,CDF 的表现非常稳定 —— 不管是预测接下来的一个 token,还是未来的数千 token,甚至是连续 token。此外,类似于全序列扩散,它也可接收引导,从而实现高奖励生成。通过协同利用因果关系、灵活的范围和可变噪声调度,CDF 能实现一项新功能:蒙特卡洛树引导(MCTG)。相比于非因果全序列扩散模型,MCTG 能极大提升高奖励生成的采样率。图 1 给出了这些能力的概况。首先,我们可以将任意 token 集合(不管是否为序列)视为一个通过 t 索引的有序集合。那么,使用教师强制(teacher forcing)训练下一 token 预测便可被解释成掩蔽掉时间 t 的每个 token x_t 基于过去 x_{1:t−1} 预测它们。对于序列,可将这种操作描述成:沿时间轴执行掩码。我们可以将全序列前向扩散(即逐渐向数据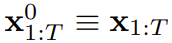 添加噪声的过程)看作一种部分掩码(partial masking),这可被称为「沿噪声轴执行掩码)。事实上,在 K 步加噪之后,
添加噪声的过程)看作一种部分掩码(partial masking),这可被称为「沿噪声轴执行掩码)。事实上,在 K 步加噪之后, (大概)就是白噪声了,不再有任何有关原数据的信息。如图 2 所示,该团队建立了一个统一视角来看待沿这两个轴的掩码。扩散强制(DF)框架可用于训练和采样任意序列长度的有噪声 token
(大概)就是白噪声了,不再有任何有关原数据的信息。如图 2 所示,该团队建立了一个统一视角来看待沿这两个轴的掩码。扩散强制(DF)框架可用于训练和采样任意序列长度的有噪声 token 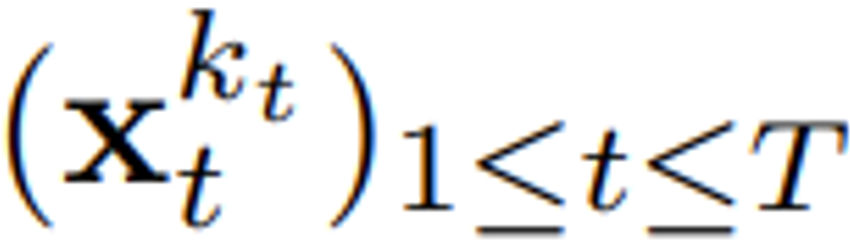 ,其中的关键在于每个 token 的噪声水平 k_t 会随时间步骤而变化。这篇论文关注的重点是时间序列数据,因此他们通过一种因果架构实例化了 DF,并由此得到了因果扩散强制(CDF)。简单来说,这是使用基础循环神经网络(RNN)获得的一种最小实现。权重为 θ 的 RNN 维护着获悉过去 token 影响的隐藏状态 z_t,其会通过一个循环层根据动态
,其中的关键在于每个 token 的噪声水平 k_t 会随时间步骤而变化。这篇论文关注的重点是时间序列数据,因此他们通过一种因果架构实例化了 DF,并由此得到了因果扩散强制(CDF)。简单来说,这是使用基础循环神经网络(RNN)获得的一种最小实现。权重为 θ 的 RNN 维护着获悉过去 token 影响的隐藏状态 z_t,其会通过一个循环层根据动态 而演化。Lorsqu'une observation de bruit d'entrée
而演化。Lorsqu'une observation de bruit d'entrée 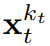 est obtenue, l'état caché est mis à jour de manière markovienne. Quand k_t=0, c'est la mise à jour postérieure du filtrage bayésien ; et quand k_t=K (bruit pur, aucune information), cela équivaut à la modélisation du filtrage bayésien p_θ(z_t | z_{. t−1}). Étant donné l'état caché z_t, le but du modèle d'observation p_θ(x_t^0 | z_t) est de prédire x_t ; le comportement entrée-sortie de cette unité est le même que le modèle de diffusion conditionnelle standard : avec le la variable de condition z_{t−1 } et le jeton bruyant en entrée, prédisent le x_t=x_t^0 silencieux, et prédisent ainsi indirectement le bruit ε^{k_t} via un reparamétrage affine. Par conséquent, nous pouvons directement utiliser la cible de diffusion classique pour entraîner le forçage de diffusion (causal). Selon le résultat de prédiction du bruit ε_θ, l'unité ci-dessus peut être paramétrée. Ensuite, les paramètres θ sont trouvés en minimisant la perte suivante :
est obtenue, l'état caché est mis à jour de manière markovienne. Quand k_t=0, c'est la mise à jour postérieure du filtrage bayésien ; et quand k_t=K (bruit pur, aucune information), cela équivaut à la modélisation du filtrage bayésien p_θ(z_t | z_{. t−1}). Étant donné l'état caché z_t, le but du modèle d'observation p_θ(x_t^0 | z_t) est de prédire x_t ; le comportement entrée-sortie de cette unité est le même que le modèle de diffusion conditionnelle standard : avec le la variable de condition z_{t−1 } et le jeton bruyant en entrée, prédisent le x_t=x_t^0 silencieux, et prédisent ainsi indirectement le bruit ε^{k_t} via un reparamétrage affine. Par conséquent, nous pouvons directement utiliser la cible de diffusion classique pour entraîner le forçage de diffusion (causal). Selon le résultat de prédiction du bruit ε_θ, l'unité ci-dessus peut être paramétrée. Ensuite, les paramètres θ sont trouvés en minimisant la perte suivante : 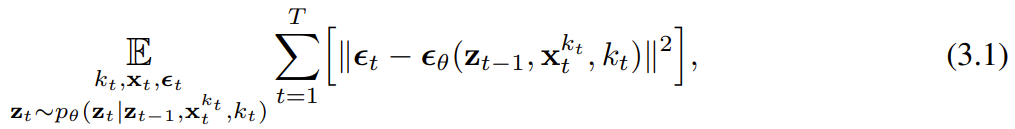 L'algorithme 1 donne le pseudocode. Le fait est que cette perte capture les éléments clés du filtrage bayésien et de la diffusion conditionnelle. L’équipe a également réinféré les techniques courantes utilisées dans la formation des modèles de diffusion pour le forçage de diffusion, comme détaillé dans l’annexe de l’article original. Ils sont également parvenus à un théorème informel. Théorème 3.1 (informel). La procédure d'entraînement forcé par diffusion (algorithme 1) est une repondération qui optimise la limite inférieure des preuves (ELBO) sur le log-vraisemblance attendue
L'algorithme 1 donne le pseudocode. Le fait est que cette perte capture les éléments clés du filtrage bayésien et de la diffusion conditionnelle. L’équipe a également réinféré les techniques courantes utilisées dans la formation des modèles de diffusion pour le forçage de diffusion, comme détaillé dans l’annexe de l’article original. Ils sont également parvenus à un théorème informel. Théorème 3.1 (informel). La procédure d'entraînement forcé par diffusion (algorithme 1) est une repondération qui optimise la limite inférieure des preuves (ELBO) sur le log-vraisemblance attendue 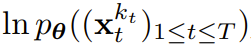 , où la valeur attendue est moyennée sur le niveau de bruit et
, où la valeur attendue est moyennée sur le niveau de bruit et 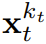 est bruyante selon un processus direct. De plus, dans des conditions appropriées, l’optimisation (3.1) peut également maximiser simultanément la limite inférieure de vraisemblance de toutes les séquences de niveaux de bruit. Échantillonnage forcé par diffusion et capacités qui en résultentL'algorithme 2 décrit le processus d'échantillonnage, qui est défini comme : dans une grille M × T bidimensionnelle K ∈ [K]^{M×T } spécifie le programme de bruit où les colonnes correspondent aux pas de temps t et les lignes indexées par m déterminent le niveau de bruit. Afin de générer la séquence entière de longueur T, le jeton x_{1:T} est d'abord initialisé au bruit blanc, correspondant au niveau de bruit k = K. Il parcourt ensuite la grille ligne par ligne et débruite colonne par colonne de gauche à droite jusqu'à ce que le niveau de bruit atteigne K. Au moment où m = 0 dans la dernière ligne, le bruit du jeton a été nettoyé, c'est-à-dire que le niveau de bruit est K_{0,t} ≡ 0. Ce paradigme d'échantillonnage apportera les nouvelles capacités suivantes :
est bruyante selon un processus direct. De plus, dans des conditions appropriées, l’optimisation (3.1) peut également maximiser simultanément la limite inférieure de vraisemblance de toutes les séquences de niveaux de bruit. Échantillonnage forcé par diffusion et capacités qui en résultentL'algorithme 2 décrit le processus d'échantillonnage, qui est défini comme : dans une grille M × T bidimensionnelle K ∈ [K]^{M×T } spécifie le programme de bruit où les colonnes correspondent aux pas de temps t et les lignes indexées par m déterminent le niveau de bruit. Afin de générer la séquence entière de longueur T, le jeton x_{1:T} est d'abord initialisé au bruit blanc, correspondant au niveau de bruit k = K. Il parcourt ensuite la grille ligne par ligne et débruite colonne par colonne de gauche à droite jusqu'à ce que le niveau de bruit atteigne K. Au moment où m = 0 dans la dernière ligne, le bruit du jeton a été nettoyé, c'est-à-dire que le niveau de bruit est K_{0,t} ≡ 0. Ce paradigme d'échantillonnage apportera les nouvelles capacités suivantes :
- Génération autorégressive stable
- Gardez l'avenir incertain
- Capacité de guidage à long terme
Utilisez le forçage de diffusion pour des décisions de séquence flexiblesLa nouvelle capacité de forçage de diffusion apporte également de nouvelles possibilités. Sur cette base, l’équipe a conçu un nouveau cadre pour la prise de décision séquentielle (SDM) et l’a appliqué avec succès aux domaines des robots et des agents autonomes. Tout d'abord, définissez un processus de décision markovien avec p dynamique (s_{t+1}|s_t, a_t), observation p (o_t|s_t) et récompense p (r_t|s_t, a_t) . Le but ici est de former une politique π(a_t|o_{1:t}) pour maximiser la récompense cumulée attendue de la trajectoire 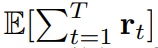 . Ici, le jeton x_t = [a_t, r_t, o_{t+1}] est alloué. Une trajectoire est une séquence x_{1:T}, dont la longueur peut être variable ; la méthode d'entraînement est celle présentée dans l'algorithme 1. A chaque étape t du processus d'exécution, il existe un état caché z_{t-1} résumant le jeton sans bruit passé x_{1:t-1}.Sur la base de cet état caché, un plan
. Ici, le jeton x_t = [a_t, r_t, o_{t+1}] est alloué. Une trajectoire est une séquence x_{1:T}, dont la longueur peut être variable ; la méthode d'entraînement est celle présentée dans l'algorithme 1. A chaque étape t du processus d'exécution, il existe un état caché z_{t-1} résumant le jeton sans bruit passé x_{1:t-1}.Sur la base de cet état caché, un plan 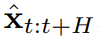 est échantillonné selon l'algorithme 2, où
est échantillonné selon l'algorithme 2, où 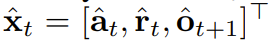 contient des actions, des récompenses et des observations prédites. H est une fenêtre d'observation vers l'avant, similaire aux prédictions futures du contrôle prédictif du modèle. Après avoir effectué l'action planifiée, l'environnement reçoit une récompense et l'observation suivante, et donc le prochain jeton. L'état caché peut être mis à jour en fonction du p_θ(z_t|z_{t−1}, x_t, 0) postérieur. Le cadre peut être utilisé à la fois comme stratégie et comme planificateur, et ses avantages incluent :
contient des actions, des récompenses et des observations prédites. H est une fenêtre d'observation vers l'avant, similaire aux prédictions futures du contrôle prédictif du modèle. Après avoir effectué l'action planifiée, l'environnement reçoit une récompense et l'observation suivante, et donc le prochain jeton. L'état caché peut être mis à jour en fonction du p_θ(z_t|z_{t−1}, x_t, 0) postérieur. Le cadre peut être utilisé à la fois comme stratégie et comme planificateur, et ses avantages incluent :
- avec des horizons de planification flexibles
- permet des conseils de récompense flexibles
- peut être atteint Monte Carlo Tree Guidance (MCTG) pour atteindre l'incertitude future
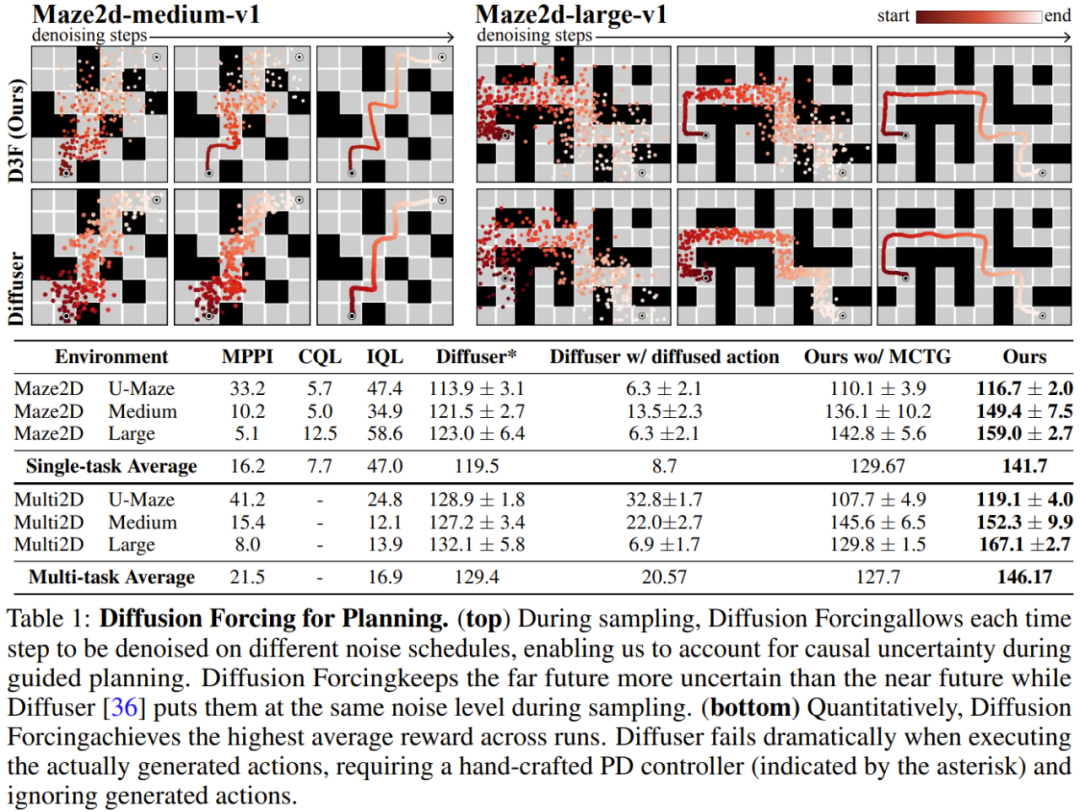
L'équipe a évalué les avantages du forçage de diffusion en tant que modèle de séquence génératif impliquant la prévision, la planification et l'apprentissage par imitation de vidéos et de séries chronologiques et autres applications. Prédiction vidéo : génération de séquences cohérentes et stables et expansion infinie Pour la tâche de modélisation générative vidéo, ils ont formé un RNN convolutif pour l'application de la diffusion causale basé sur les vidéos de jeux Minecraft et les réalisations de navigation DMLab. La figure 3 montre les résultats qualitatifs du forçage de diffusion par rapport à la ligne de base. On peut voir que le forçage de diffusion peut se déployer de manière stable, même au-delà de sa plage de formation, tandis que les repères de forçage des enseignants et de diffusion en séquence complète divergent rapidement. Planification de la diffusion : MCTG, incertitude causale, contrôle flexible de la portéeLa capacité de diffuser le forçage peut apporter des avantages uniques à la prise de décision. L'équipe a évalué le cadre de prise de décision nouvellement proposé à l'aide de D4RL, un cadre standard d'apprentissage par renforcement hors ligne. Le Tableau 1 donne les résultats de l'évaluation qualitative et quantitative. Comme on peut le constater, Diffusion Enforcement surpasse Diffuser et toutes les lignes de base dans les 6 environnements. Génération de combinaisons de séquences contrôlables L'équipe a découvert qu'il est possible de combiner de manière flexible des sous-séquences de séquences observées au moment de l'entraînement simplement en modifiant le schéma d'échantillonnage. Ils ont mené des expériences en utilisant un ensemble de données de trajectoire 2D : sur un plan carré, toutes les trajectoires partent d'un coin et se terminent au coin opposé, formant une sorte de forme de croix. Comme le montre la figure 1 ci-dessus, lorsque le comportement de combinaison n'est pas requis, DF peut être autorisé à conserver une mémoire complète et à reproduire la distribution du croisement. Lorsqu'une combinaison est nécessaire, le modèle peut être utilisé pour générer des plans plus courts sans mémoire à l'aide de MPC, assemblant ainsi les sous-trajectoires de cette croix pour obtenir une trajectoire en forme de V. Robots : apprentissage par imitation à longue portée et contrôle visuel robuste des mouvementsLe forçage par diffusion offre également de nouvelles opportunités pour le contrôle visuel des mouvements de vrais robots. L'apprentissage par imitation est une technique de contrôle de robot couramment utilisée qui apprend les cartographies des actions observées démontrées par des experts. Cependant, le manque de mémoire rend souvent l’apprentissage par imitation difficile pour les tâches à longue portée. DF peut non seulement atténuer cette lacune, mais également rendre l’apprentissage par imitation plus robuste. Utilisez la mémoire pour l'apprentissage par imitation. En contrôlant à distance le robot Franka, l’équipe a collecté un ensemble de données vidéo et de mouvement. Comme le montre la figure 4, la tâche consiste à échanger les positions des pommes et des oranges en utilisant la troisième position. La position initiale du fruit est aléatoire, il existe donc deux états cibles possibles. De plus, lorsqu'il y a un fruit en troisième position, le résultat souhaité ne peut pas être déduit de l'observation actuelle - la stratégie doit mémoriser la configuration initiale afin de décider quel fruit déplacer.Contrairement aux méthodes de clonage de comportement couramment utilisées, DF peut naturellement intégrer des souvenirs dans son propre état caché. Il a été constaté que DF atteignait un taux de réussite de 80 %, tandis que la stratégie de diffusion (actuellement le meilleur algorithme d’apprentissage par imitation sans mémoire) échouait.  De plus, DF peut également gérer le bruit de manière plus robuste et faciliter la pré-formation des robots. Prévision de séries chronologiques : le forçage de diffusion est un excellent modèle de séquence généralePour les tâches de prévision de séries chronologiques multivariées, les recherches de l'équipe montrent que DF est suffisant pour rivaliser avec les modèles de diffusion précédents et le modèle basé sur les transformateurs. comparable. Veuillez vous référer à l'article original pour plus de détails techniques et de résultats expérimentaux.
De plus, DF peut également gérer le bruit de manière plus robuste et faciliter la pré-formation des robots. Prévision de séries chronologiques : le forçage de diffusion est un excellent modèle de séquence généralePour les tâches de prévision de séries chronologiques multivariées, les recherches de l'équipe montrent que DF est suffisant pour rivaliser avec les modèles de diffusion précédents et le modèle basé sur les transformateurs. comparable. Veuillez vous référer à l'article original pour plus de détails techniques et de résultats expérimentaux. 以上是无限生成视频,还能规划决策,扩散强制整合下一token预测与全序列扩散的详细内容。更多信息请关注PHP中文网其他相关文章!


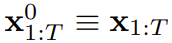 添加噪声的过程)看作一种部分掩码(partial masking),这可被称为「沿噪声轴执行掩码)。
添加噪声的过程)看作一种部分掩码(partial masking),这可被称为「沿噪声轴执行掩码)。 (大概)就是白噪声了,不再有任何有关原数据的信息。
(大概)就是白噪声了,不再有任何有关原数据的信息。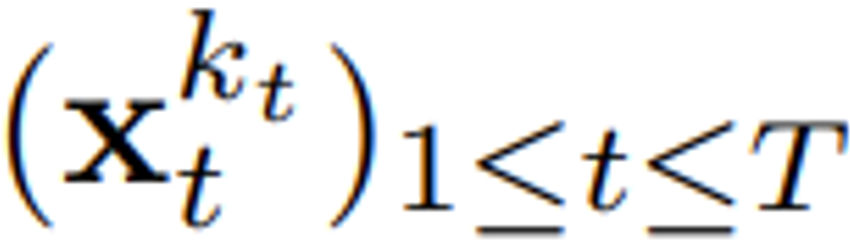 ,其中的关键在于每个 token 的噪声水平 k_t 会随时间步骤而变化。
,其中的关键在于每个 token 的噪声水平 k_t 会随时间步骤而变化。 而演化。Lorsqu'une observation de bruit d'entrée
而演化。Lorsqu'une observation de bruit d'entrée 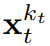 est obtenue, l'état caché est mis à jour de manière markovienne.
est obtenue, l'état caché est mis à jour de manière markovienne. 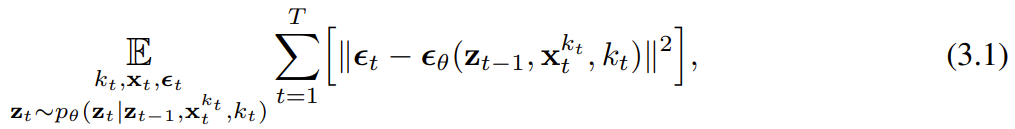

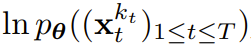 , où la valeur attendue est moyennée sur le niveau de bruit et
, où la valeur attendue est moyennée sur le niveau de bruit et 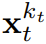 est bruyante selon un processus direct. De plus, dans des conditions appropriées, l’optimisation (3.1) peut également maximiser simultanément la limite inférieure de vraisemblance de toutes les séquences de niveaux de bruit.
est bruyante selon un processus direct. De plus, dans des conditions appropriées, l’optimisation (3.1) peut également maximiser simultanément la limite inférieure de vraisemblance de toutes les séquences de niveaux de bruit. 
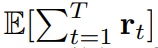 . Ici, le jeton x_t = [a_t, r_t, o_{t+1}] est alloué. Une trajectoire est une séquence x_{1:T}, dont la longueur peut être variable ; la méthode d'entraînement est celle présentée dans l'algorithme 1.
. Ici, le jeton x_t = [a_t, r_t, o_{t+1}] est alloué. Une trajectoire est une séquence x_{1:T}, dont la longueur peut être variable ; la méthode d'entraînement est celle présentée dans l'algorithme 1. 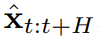 est échantillonné selon l'algorithme 2, où
est échantillonné selon l'algorithme 2, où 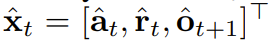 contient des actions, des récompenses et des observations prédites. H est une fenêtre d'observation vers l'avant, similaire aux prédictions futures du contrôle prédictif du modèle. Après avoir effectué l'action planifiée, l'environnement reçoit une récompense et l'observation suivante, et donc le prochain jeton. L'état caché peut être mis à jour en fonction du p_θ(z_t|z_{t−1}, x_t, 0) postérieur.
contient des actions, des récompenses et des observations prédites. H est une fenêtre d'observation vers l'avant, similaire aux prédictions futures du contrôle prédictif du modèle. Après avoir effectué l'action planifiée, l'environnement reçoit une récompense et l'observation suivante, et donc le prochain jeton. L'état caché peut être mis à jour en fonction du p_θ(z_t|z_{t−1}, x_t, 0) postérieur.