
编辑 | 绿罗
就像随风扩散、扑面而来的花香,材料中的原子与分子也在进行着它们的「扩散」。
材料中的分散决定了沉淀、新相形成和微观结构演化的动力学,并强烈影响机械和物理性能。成分复杂的材料固有的化学复杂性,给原子扩散建模和化学有序结构的形成带来了挑战。
在这方面,加州大学的研究人员提出了一种神经网络动力学(NNK)方法,用于预测成分复杂材料中的原子扩散,并由此产生的微观结构演化。
该框架基于高效的晶格结构和化学表征,结合人工神经网络,能够精确预测所有依赖于路径的迁移势垒和单个原子跳跃。可扩展的 NNK 框架为探索隐藏着非凡属性的广阔组合空间中的扩散相关属性提供了一条有前途的新途径。
相关研究以「Neural network kinetics for exploring diffusion multiplicity and chemical ordering in compositionally complex materials」为题,于 5 月 9 日发布在《Nature Communications》上。

原子从一个位置转移到另一个位置的扩散控制着许多重要的过程和行为,如沉淀和相成核。
在金属和合金中,扩散过程与介导晶格中原子跳跃的空位、点缺陷有关。基于力场或密度泛函理论的分子动力学(MD)建模可探测纳秒时间尺度的原子扩散机制,但通常无法获得缓慢扩散动力学引起的微观结构变化。
kMC模拟方法是一种用来模拟扩散介导的结构演化的技术。在kMC模拟中,由于过渡状态搜索的计算成本较高,关键参数通常从连续模型参数化。
成分复杂合金(CCA)的出现,通常被称为高熵合金,带来了许多有趣的动力学行为,包括化学短程有序、沉淀、偏析和辐射缺陷湮灭,这些行为尚未从根本上得到理解和最终预测。然而,CCA 中的化学复杂性给扩散介导过程的建模带来了新的挑战。
机器学习方法的出现证明了解决材料科学中涉及非线性相互作用和大规模组合空间的计算复杂问题的潜力。
关于成分复杂的合金中的空位扩散,一个重要的关键参数是扩散能垒 ΔE,即过渡态与初始能量最小值之间的能量差。由于 CCA 中原子尺度的成分波动和多个扩散方向的存在,需要机器学习模型来精确预测矢量属性,特别是扩散路径相关的势垒。
在该研究中,研究人员提出了一种神经网络动力学(NNK)方案,来预测和模拟复杂浓缩(concentrated)化学环境中扩散诱导的化学和结构演化。
下图 a 为晶格结构和化学表示,其中带有空位的初始原子构型被编码成数字矩阵或神经元图。数字(1、2 和 3)代表相应的原子类型,0 表示空位。然后,这些矢量化数字被传递到 NNK 模型并用作输入神经元。
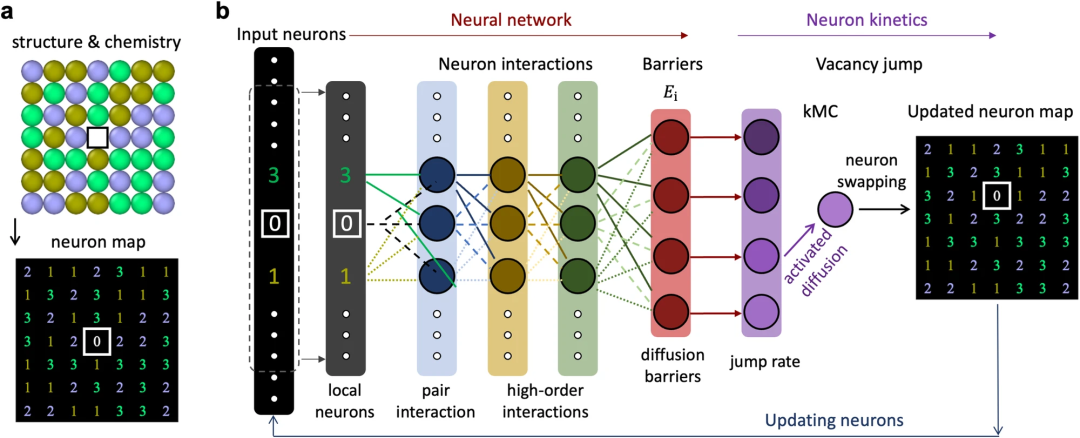
NNK 由人工神经网络和神经元动力学模块组成。引入的神经网络(具有两个以上的隐藏层)旨在学习输入神经元(即原子和空位)之间的非线性相互作用,并输出扩散能垒。值得注意的是,该网络仅使用空位及其相邻神经元作为输入,从而导致计算成本较低且恒定,而不会牺牲准确性。
神经元动力学模块采用动力学蒙特卡罗方法,利用与每条扩散路径相关的可用势垒进行扩散动力学演化。只需将原子构型一次性转换为神经元图,就可以通过交换神经图的两位数字来模拟空位跳跃和化学演化。通过这种方式,可以有效地对数百万个空位跳跃进行建模,每次跳跃迭代仅涉及两个神经元的动作。
研究人员使用 NNK 和 bcc NbMoTa 作为模型系统,探索了扩散动力学介导的化学排序和 B2 相形成,并揭示了 CCA 固有的反常扩散(扩散多重性)。
发现了临界温度的存在,在该温度下 B2(B2 晶胞具有简单的 bcc 结构,由 Ta 和 Mo 两种物质组成,有序地位于立方角或中心)有序达到最大值。化学有序的温度依赖性与潜在的晶格跳跃随机性密切相关。

在接近熔点的高温下,扩散跳跃最终接近纯粹的随机过程,对应于有序形成的低倾向。在低温下,晶格扩散由最低势垒路径主导,表现为定向跳跃并限制化学有序结构的成核。在中间范围的临界温度下,随机和定向型晶格跳跃遍布整个系统,表现出最高的扩散异质性(多重性)。
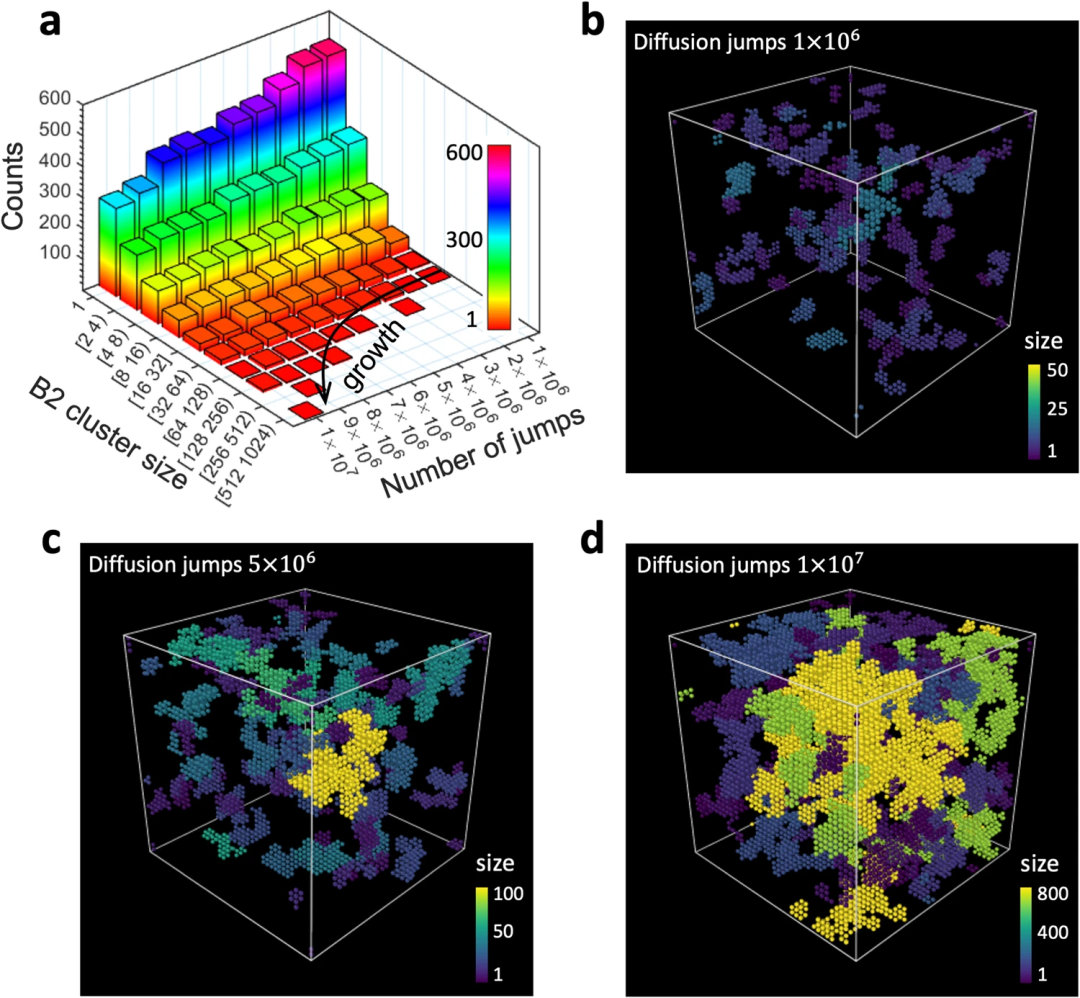
通过在退火过程中跟踪各个 B2 团簇,发现它们的成核和生长是间歇性且不均匀的,并伴随着小团簇的减少和湮灭。使用随机原子类型交换的基于虚拟热力学的建模并未捕获 B2 结构动力学增长的这一显著特征,该模型显示出更均匀的增长。
这些结果凸显了 CCA 走向稳定状态的复杂且众多的动力学途径,其中有序结构成核、湮灭、生长和重排等许多过程相互作用和协调。

对数十种成分进行训练的神经网络展示了对未见成分的高性能,揭示了 Nb-Mo-Ta 的整个三元空间。由于构图的设计空间几乎是无限的,通过混合多种元素形成的构图复杂的材料开辟了一个有待探索的新领域。
通过直接将多维成分与扩散势垒谱联系起来,NNK 为探索 CCA 的广阔成分空间指明了一条光明的道路,其中隐藏着非凡的动力学特性。
以上是探索复合材料中的原子扩散,加州大学开发神经网络动力学方法的详细内容。更多信息请关注PHP中文网其他相关文章!




