讓theta=模型參數和max_iters=時期數。對於itr=1,2,3,...,max_iters：對於mini_batch(X_mini,y_mini)：
批次X_mini的前傳遞：
##1、對小批次進行預測2、使用參數的目前值計算預測誤差(J(theta))後傳：計算梯度(theta)=J(theta)wrt theta的偏導數 #更新參數：theta=theta–learning_rate*gradient(theta)Python實現梯度下降演算法的程式碼流程第一步：導入依賴項，為線性迴歸產生數據，並視覺化產生的數據。以8000個資料範例，每個範例都有2個屬性特徵。這些資料樣本進一步分為訓練集（X_train，y_train）和測試集（X_test，y_test），分別有7200和800個樣本。import numpy as np import matplotlib.pyplot as plt mean=np.array([5.0,6.0]) cov=np.array([[1.0,0.95],[0.95,1.2]]) data=np.random.multivariate_normal(mean,cov,8000) plt.scatter(data[:500,0],data[:500,1],marker='.') plt.show() data=np.hstack((np.ones((data.shape[0],1)),data)) split_factor=0.90 split=int(split_factor*data.shape[0]) X_train=data[:split,:-1] y_train=data[:split,-1].reshape((-1,1)) X_test=data[split:,:-1] y_test=data[split:,-1].reshape((-1,1)) print(& quot Number of examples in training set= % d & quot % (X_train.shape[0])) print(& quot Number of examples in testing set= % d & quot % (X_test.shape[0]))
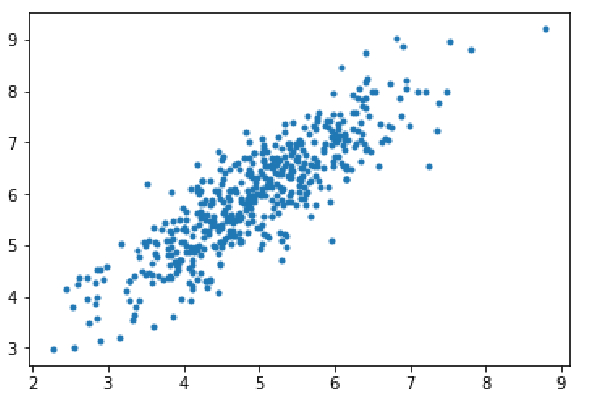訓練集中的範例數=7200測試集中的範例數=800第二步：使用小批量梯度下降實現線性迴歸的程式碼。 gradientDescent()是主要的驅動函數，其他函數是輔助函數：進行預測－hypothesis()#計算梯度－gradient()##計算誤差— —cost()
建立小批量－create_mini_batches()
驅動程式函數初始化參數，計算模型的最佳參數集，並傳回這些參數以及一個列表，其中包含參數更新時的錯誤歷史記錄。
def hypothesis(X,theta):
return np.dot(X,theta)
def gradient(X,y,theta):
h=hypothesis(X,theta)
grad=np.dot(X.transpose(),(h-y))
return grad
def cost(X,y,theta):
h=hypothesis(X,theta)
J=np.dot((h-y).transpose(),(h-y))
J/=2
return J[0]
def create_mini_batches(X,y,batch_size):
mini_batches=[]
data=np.hstack((X,y))
np.random.shuffle(data)
n_minibatches=data.shape[0]//batch_size
i=0
for i in range(n_minibatches+1):
mini_batch=data[i*batch_size:(i+1)*batch_size,:]
X_mini=mini_batch[:,:-1]
Y_mini=mini_batch[:,-1].reshape((-1,1))
mini_batches.append((X_mini,Y_mini))
if data.shape[0]%batch_size!=0:
mini_batch=data[i*batch_size:data.shape[0]]
X_mini=mini_batch[:,:-1]
Y_mini=mini_batch[:,-1].reshape((-1,1))
mini_batches.append((X_mini,Y_mini))
return mini_batches
def gradientDescent(X,y,learning_rate=0.001,batch_size=32):
theta=np.zeros((X.shape[1],1))
error_list=[]
max_iters=3
for itr in range(max_iters):
mini_batches=create_mini_batches(X,y,batch_size)
for mini_batch in mini_batches:
X_mini,y_mini=mini_batch
theta=theta-learning_rate*gradient(X_mini,y_mini,theta)
error_list.append(cost(X_mini,y_mini,theta))
return theta,error_list呼叫gradientDescent()函數來計算模型參數(theta)並視覺化誤差函數的變化。
theta,error_list=gradientDescent(X_train,y_train)
print("Bias=",theta[0])
print("Coefficients=",theta[1:])
plt.plot(error_list)
plt.xlabel("Number of iterations")
plt.ylabel("Cost")
plt.show()偏差=[0.81830471]係數=[[1.04586595]]
第三步：對測試集進行預測併計算預測中的平均絕對誤差。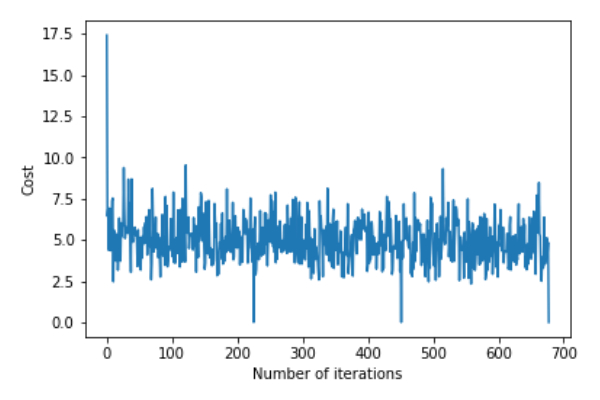
y_pred=hypothesis(X_test,theta) plt.scatter(X_test[:,1],y_test[:,],marker='.') plt.plot(X_test[:,1],y_pred,color='orange') plt.show() error=np.sum(np.abs(y_test-y_pred)/y_test.shape[0]) print(& quot Mean absolute error=",error)
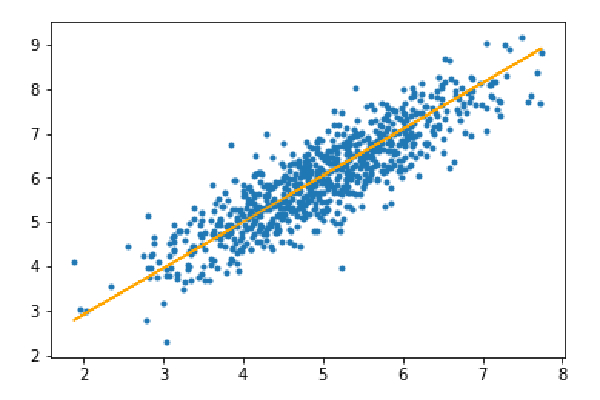
橘色線代表最終假設函數：theta[0] theta[1]*X_test[:,1] theta[2]*X_test[ :,2]=0
以上是使用Python實現小批量梯度下降演算法的程式碼邏輯的詳細內容。更多資訊請關注PHP中文網其他相關文章！
