在機器學習中,術語Ensemble指的是平行組合多個模型,這個想法是利用群體的智慧,在給出的最終答案上形成更好的共識。

在監督學習領域,已經廣泛研究和應用了這種方法,尤其是在分類問題上,像RandomForest這樣非常成功的演算法。通常會採用投票/加權系統,將每個單獨模型的輸出組合成更健壯和一致的最終輸出
在無監督學習領域,這項任務變得更加困難。首先,因為它包含了該領域本身的挑戰,我們對數據沒有先驗知識,無法將自己與任何目標進行比較。其次,因為找到合適的方法來結合所有模型的資訊仍然是一個問題,而且對於如何做到這一點還沒有共識。
在本文中,我們討論關於這個主題的最佳方法,即相似性矩陣的聚類。
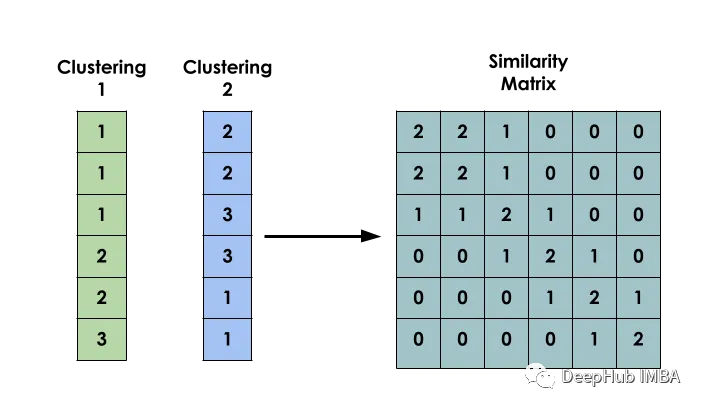
該方法的主要想法是:給定一個資料集X,建立一個矩陣S,使得Si表示xi和xj之間的相似性。此矩陣是基於幾個不同模型的聚類結果建構的。
建立輸入之間的二元共現矩陣是建立模型的第一步

它用於指示兩個輸入i和j是否屬於同一個簇。
import numpy as np from scipy import sparse def build_binary_matrix( clabels ): data_len = len(clabels) matrix=np.zeros((data_len,data_len))for i in range(data_len):matrix[i,:] = clabels == clabels[i]return matrix labels = np.array( [1,1,1,2,3,3,2,4] ) build_binary_matrix(labels)
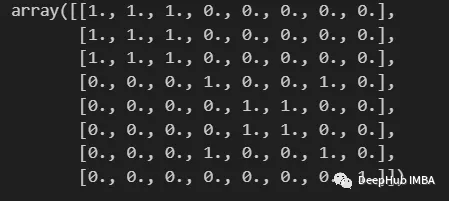
我們已經建構了一個函數來二值化我們的聚類,下面可以進入建構相似矩陣的階段。
我們在這裡介紹一個常見的方法,它只涉及計算M個不同模型產生的M個共現矩陣之間的平均值。我們將其定義為:

當條目落在同一簇中時,它們的相似度值將接近1,而當條目落在不同群組中時,它們的相似度值將接近0
我們將基於K-Means模型建立的標籤建立一個相似矩陣。使用MNIST資料集進行。為了簡單和高效,我們將只使用10000張經過PCA降維的影像。
from sklearn.datasets import fetch_openml from sklearn.decomposition import PCA from sklearn.cluster import MiniBatchKMeans, KMeans from sklearn.model_selection import train_test_split mnist = fetch_openml('mnist_784') X = mnist.data y = mnist.target X, _, y, _ = train_test_split(X,y, train_size=10000, stratify=y, random_state=42 ) pca = PCA(n_components=0.99) X_pca = pca.fit_transform(X)
為了讓模型之間存在多樣性,每個模型都使用隨機數量的簇實例化。
NUM_MODELS = 500 MIN_N_CLUSTERS = 2 MAX_N_CLUSTERS = 300 np.random.seed(214) model_sizes = np.random.randint(MIN_N_CLUSTERS, MAX_N_CLUSTERS+1, size=NUM_MODELS) clt_models = [KMeans(n_clusters=i, n_init=4, random_state=214) for i in model_sizes] for i, model in enumerate(clt_models):print( f"Fitting - {i+1}/{NUM_MODELS}" )model.fit(X_pca)
下面的函數就是建立相似矩陣
def build_similarity_matrix( models_labels ):n_runs, n_data = models_labels.shape[0], models_labels.shape[1] sim_matrix = np.zeros( (n_data, n_data) ) for i in range(n_runs):sim_matrix += build_binary_matrix( models_labels[i,:] ) sim_matrix = sim_matrix/n_runs return sim_matrix
呼叫這個函數:
models_labels = np.array([ model.labels_ for model in clt_models ]) sim_matrix = build_similarity_matrix(models_labels)
最終結果如下:
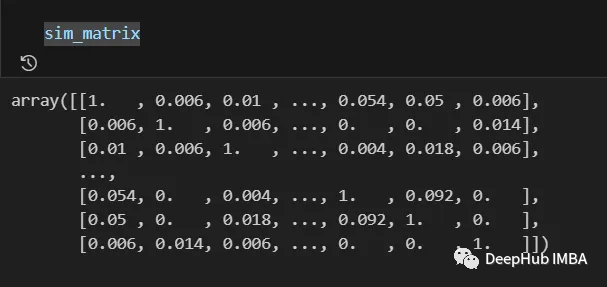
來自相似矩陣的資訊在最後一步之前仍然可以進行後處理,例如應用對數、多項式等變換。
在我們的情況下,我們將保持原意不變進行重寫
Pos_sim_matrix = sim_matrix
相似矩陣是一種表示所有聚類模型協作所建立的知識的方法。
我們可以透過它直觀地看到哪些條目更有可能屬於同一個簇,哪些不屬於。然而,這些資訊仍然需要轉換為實際的簇
這是透過使用可以接收相似矩陣作為參數的聚類演算法來完成的。這裡我們使用SpectralClustering。
from sklearn.cluster import SpectralClustering spec_clt = SpectralClustering(n_clusters=10, affinity='precomputed',n_init=5, random_state=214) final_labels = spec_clt.fit_predict(pos_sim_matrix)
我們來與KMeans進行性對比,這樣可以確認我們的方法是否有效。
我們將使用NMI、ARI、群集純度和類別純度指標來評估標準的KMeans模型和我們的整合模型進行比較。此外,我們還將繪製權變矩陣,以視覺化每個簇中屬於哪些類別
from seaborn import heatmap import matplotlib.pyplot as plt def data_contingency_matrix(true_labels, pred_labels): fig, (ax) = plt.subplots(1, 1, figsize=(8,8)) n_clusters = len(np.unique(pred_labels))n_classes = len(np.unique(true_labels))label_names = np.unique(true_labels)label_names.sort() contingency_matrix = np.zeros( (n_classes, n_clusters) ) for i, true_label in enumerate(label_names):for j in range(n_clusters):contingency_matrix[i, j] = np.sum(np.logical_and(pred_labels==j, true_labels==true_label)) heatmap(contingency_matrix.astype(int), ax=ax,annot=True, annot_kws={"fontsize":14}, fmt='d') ax.set_xlabel("Clusters", fontsize=18)ax.set_xticks( [i+0.5 for i in range(n_clusters)] )ax.set_xticklabels([i for i in range(n_clusters)], fontsize=14) ax.set_ylabel("Original classes", fontsize=18)ax.set_yticks( [i+0.5 for i in range(n_classes)] )ax.set_yticklabels(label_names, fontsize=14, va="center") ax.set_title("Contingency Matrix\n", ha='center', fontsize=20)
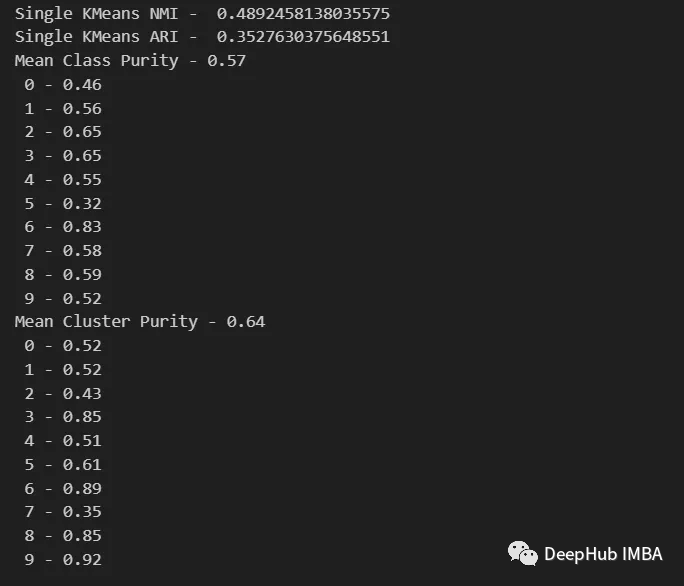
from sklearn.metrics import normalized_mutual_info_score, adjusted_rand_score def purity( true_labels, pred_labels ): n_clusters = len(np.unique(pred_labels))n_classes = len(np.unique(true_labels))label_names = np.unique(true_labels) purity_vector = np.zeros( (n_classes) )contingency_matrix = np.zeros( (n_classes, n_clusters) ) for i, true_label in enumerate(label_names):for j in range(n_clusters):contingency_matrix[i, j] = np.sum(np.logical_and(pred_labels==j, true_labels==true_label)) purity_vector = np.max(contingency_matrix, axis=1)/np.sum(contingency_matrix, axis=1) print( f"Mean Class Purity - {np.mean(purity_vector):.2f}" ) for i, true_label in enumerate(label_names):print( f" {true_label} - {purity_vector[i]:.2f}" ) cluster_purity_vector = np.zeros( (n_clusters) )cluster_purity_vector = np.max(contingency_matrix, axis=0)/np.sum(contingency_matrix, axis=0) print( f"Mean Cluster Purity - {np.mean(cluster_purity_vector):.2f}" ) for i in range(n_clusters):print( f" {i} - {cluster_purity_vector[i]:.2f}" ) kmeans_model = KMeans(10, n_init=50, random_state=214) km_labels = kmeans_model.fit_predict(X_pca) data_contingency_matrix(y, km_labels) print( "Single KMeans NMI - ", normalized_mutual_info_score(y, km_labels) ) print( "Single KMeans ARI - ", adjusted_rand_score(y, km_labels) ) purity(y, km_labels)
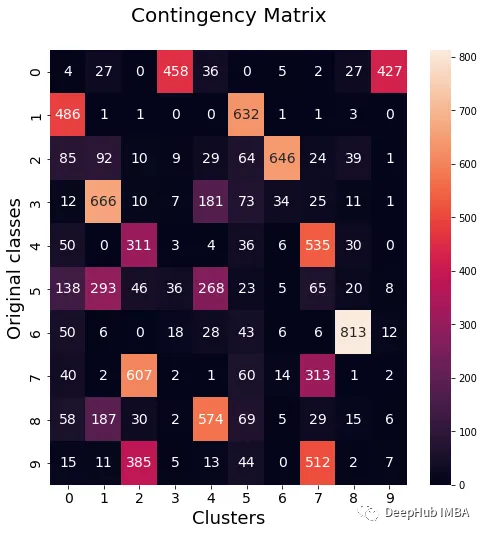
data_contingency_matrix(y, final_labels) print( "Ensamble NMI - ", normalized_mutual_info_score(y, final_labels) ) print( "Ensamble ARI - ", adjusted_rand_score(y, final_labels) ) purity(y, final_labels)
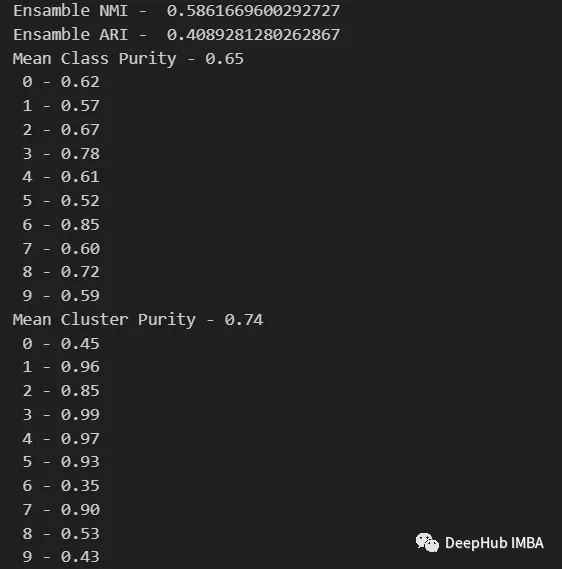
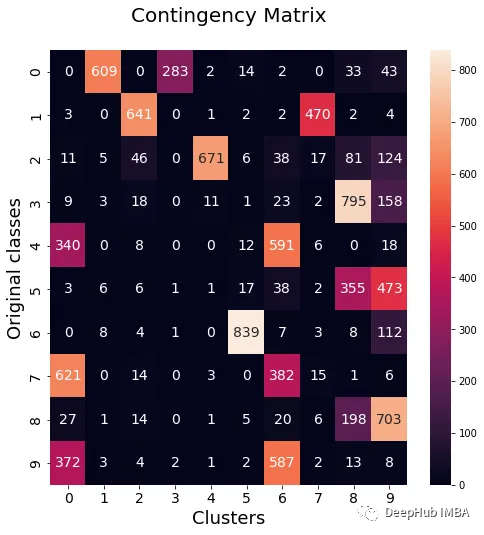
透過觀察上述數值,可以明顯看出Ensemble方法能夠有效提升聚類的品質。同時,在權變矩陣中也能觀察到更一致的行為,具有較好的分佈類別和較少的「雜訊」
以上是無監督學習的整合方法:相似性矩陣的聚類的詳細內容。更多資訊請關注PHP中文網其他相關文章!