線性迴歸有四個假設:
殘差是指預測值與觀測值之間的誤差。它測量數據點與迴歸線的距離。它是透過從觀察值中減去預測值的計算機。
殘差圖是評估迴歸模型的好方法。它是一個圖表,在垂直軸上顯示所有殘差,在 x 軸上顯示特徵。如果數據點隨機散佈在沒有圖案的線上,那麼線性迴歸模型非常適合數據,否則我們應該使用非線性模型。
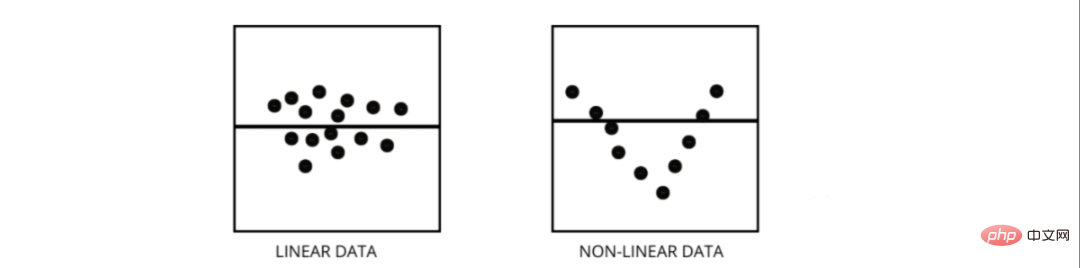
兩者都是迴歸問題的型別。兩者的差別在於他們訓練的數據。
線性迴歸模型假設特徵和標籤之間存在線性關係,這表示如果我們取得所有資料點並將它們繪製成線性(直線)線應該適合資料。
非線性迴歸模型假設變數之間沒有線性關係。非線性(曲線)線應該能夠正確地分離和擬合數據。
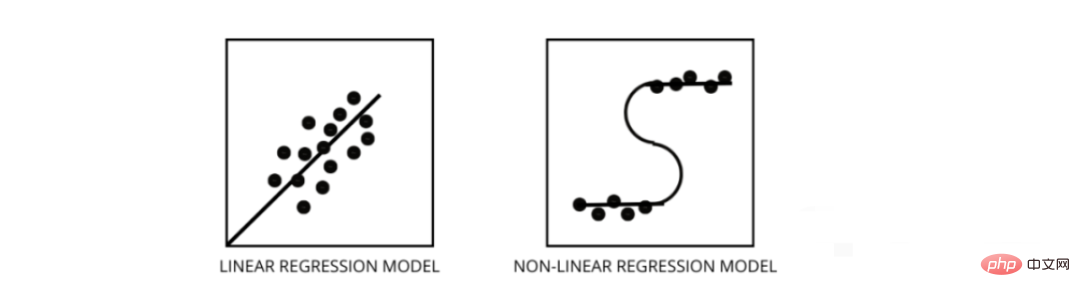
找出資料是線性還是非線性的三種最佳方法-
當某些特徵彼此高度相關時,就會發生多重共線性。相關性是指表示一個變數如何受到另一個變數變化影響的量測。
如果特徵 a 的增加導致特徵 b 的增加,那麼這兩個特徵是正相關的。如果 a 的增加導致特徵 b 的減少,那麼這兩個特徵是負相關的。在訓練資料上有兩個高度相關的變數會導致多重共線性,因為它的模型無法在資料中找到模式,從而導致模型表現不佳。所以在訓練模型之前首先要盡量消除多重共線性。
異常值是值與資料點的平均值範圍不同的資料點。換句話說,這些點與數據不同或在第 3 標準之外。
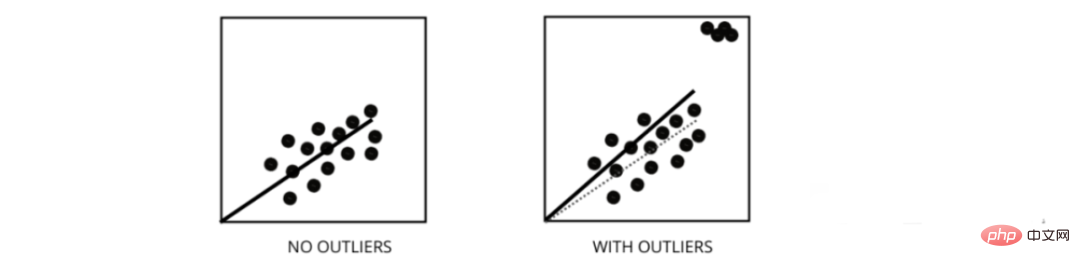
線性迴歸模型試圖找出一條可以減少殘差的最佳擬合線。如果資料包含異常值,則最佳擬合線將向異常值移動一點,從而增加錯誤率並得出具有非常高 MSE 的模型。
MSE 代表均方誤差,它是實際值和預測值之間的平方差。而 MAE 是目標值和預測值之間的絕對差。
MSE 會懲罰大錯誤,而 MAE 不會。隨著 MSE 和 MAE 的值都降低,模型趨向於一條更好的擬合線。
在機器學習中,我們的主要目標是創建一個可以在訓練和測試資料上表現更好的通用模型,但是在資料非常少的情況下,基本的線性迴歸模型往往會過度擬合,因此我們會使用l1 和l2 正規化。
L1 正規化或 lasso 迴歸透過在成本函數內添加添加斜率的絕對值作為懲罰項。有助於透過刪除斜率值小於閾值的所有資料點來去除異常值。
L2 正規化或ridge 迴歸增加了相當於係數大小平方的懲罰項。它會懲罰具有較高斜率值的特徵。
l1 和 l2 在訓練資料較少、變異數高、預測特徵大於觀察值、資料存在多重共線性的情況下都很有用。
它是指最佳擬合線周圍的資料點的變異數在一個範圍內不一樣的情況。它導致殘差的不均勻分散。如果它存在於資料中,那麼模型傾向於預測無效輸出。檢定異方差的最好方法之一是繪製殘差圖。
資料內部異方差的最大原因之一是範圍特徵之間的巨大差異。例如,如果我們有一個從1 到100000 的列,那麼將值增加10% 不會改變較低的值,但在較高的值時則會產生非常大的差異,從而產生很大的方差差異的數據點。
變異數膨脹因子(vif)用於找出使用其他自變數可預測自變數的程度。
讓我們以具有 v1、v2、v3、v4、v5 和 v6 特徵的範例資料為例。現在,為了計算 v1 的 vif,將其視為預測變量,並嘗試使用所有其他預測變量對其進行預測。
如果 VIF 的值很小,那麼最好從資料中刪除該變數。因為較小的值表示變數之間的高相關性。
逐步迴歸是在假設檢定的幫助下,透過移除或加入預測變數來建立迴歸模型的一種方法。它透過迭代檢驗每個自變量的顯著性來預測因變量,並在每次迭代之後刪除或添加一些特徵。它運行n次,並試圖找到最佳的參數組合,以預測因變數的觀測值和預測值之間的誤差最小。
它可以非常有效率地管理大量數據,並解決高維度問題。

我們用一個迴歸問題來介紹這些指標,我們的其中輸入是工作經驗,輸出是薪水。下圖顯示了為預測薪水而繪製的線性迴歸線。
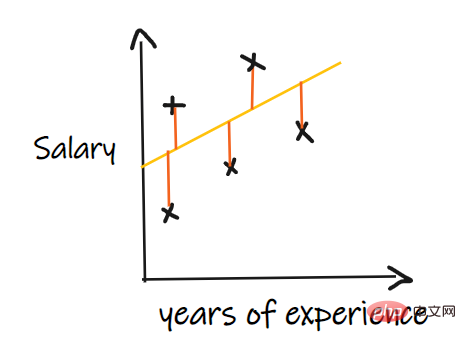
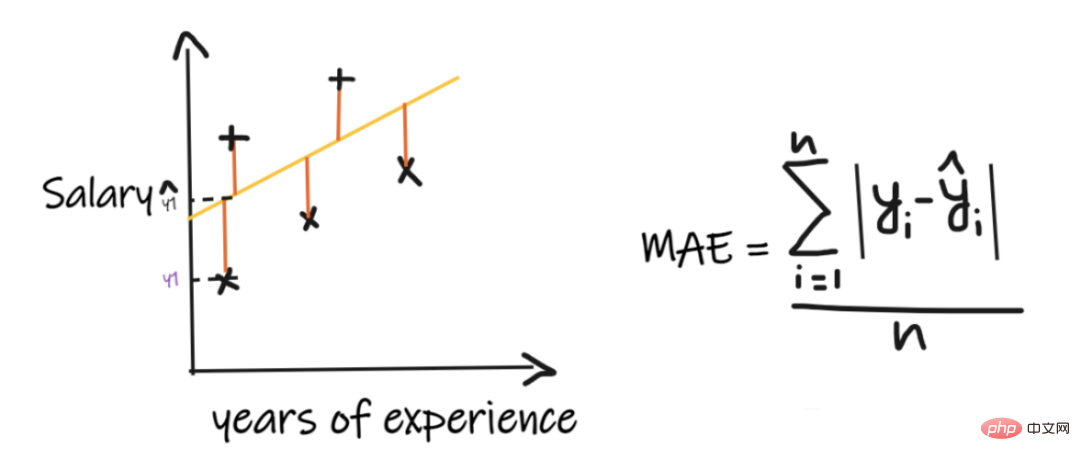
平均絕對誤差(MAE) 是最簡單的迴歸度量。它將每個實際值和預測值的差異相加,最後除以觀察次數。為了使迴歸模型被認為是一個好的模型,MAE 應該盡可能小。
簡單易懂。結果將具有與輸出相同的單位。例如:如果輸出列的單位是LPA,那麼如果MAE 為1.2,那麼我們可以解釋結果是1.2LPA 或-1.2LPA,MAE 對異常值相對穩定(與其他一些迴歸指標相比,MAE 受異常值的影響較小)。
MAE使用的是模函數,但模函數不是在所有點都可微的,所以很多情況下不能作為損失函數。
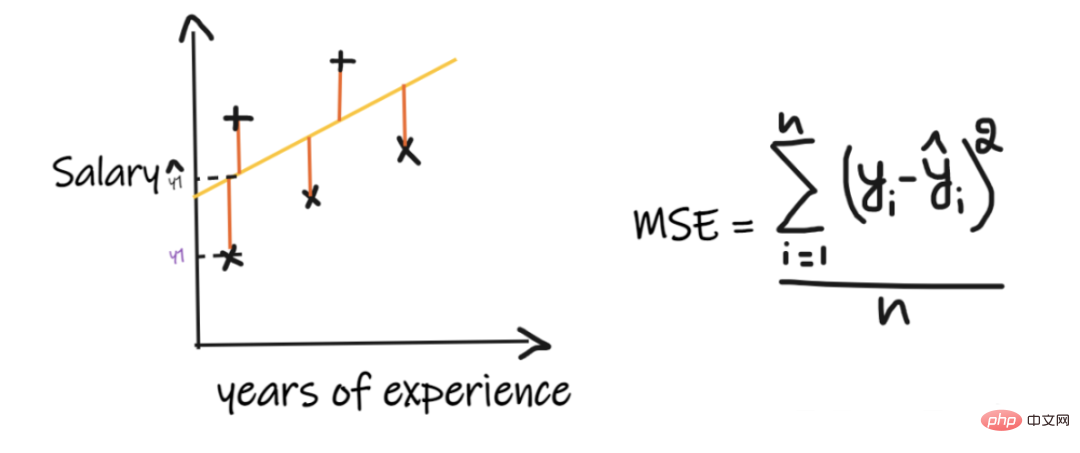
MSE取每個實際值和預測值之間的差異,然後將差異平方並將它們相加,最後除以觀測數量。為了使迴歸模型被認為是一個好的模型,MSE 應該盡可能小。
MSE的優點:平方函數在所有點上都是可微的,因此它可以用作損失函數。
MSE的缺點:由於 MSE 使用平方函數,結果的單位是輸出的平方。因此很難解釋結果。由於它使用平方函數,如果資料中有異常值,則差異也會被平方,因此,MSE 對異常值不穩定。
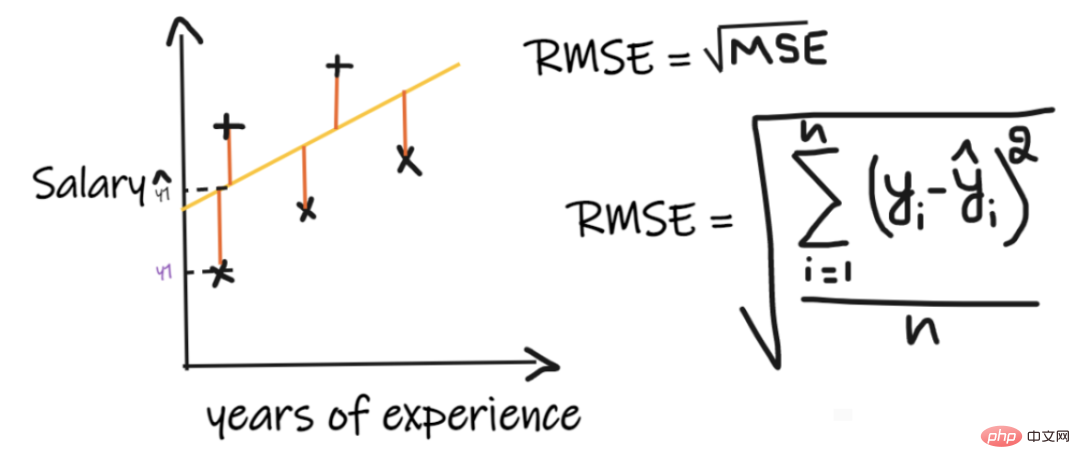
#均方根誤差(RMSE)取每個實際值和預測值之間的差值,然後將差異平方並將它們相加,最後除以觀測數量。然後取結果的平方根。因此,RMSE 是 MSE 的平方根。為了使迴歸模型被認為是一個好的模型,RMSE 應該盡可能小。
RMSE 解決了 MSE 的問題,單位將與輸出的單位相同,因為它取平方根,但仍然對異常值不那麼穩定。
上述指標取決於我們正在解決的問題的上下文, 我們不能在不了解實際問題的情況下,只看 MAE、MSE 和 RMSE 的值來判斷模型的好壞。
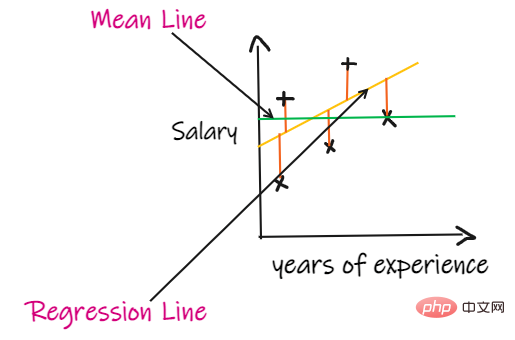
如果我們沒有任何輸入數據,但是想知道他在這家公司能拿到多少薪水,那麼我們能做的最好的事情就是給他們所有員工薪水的平均值。
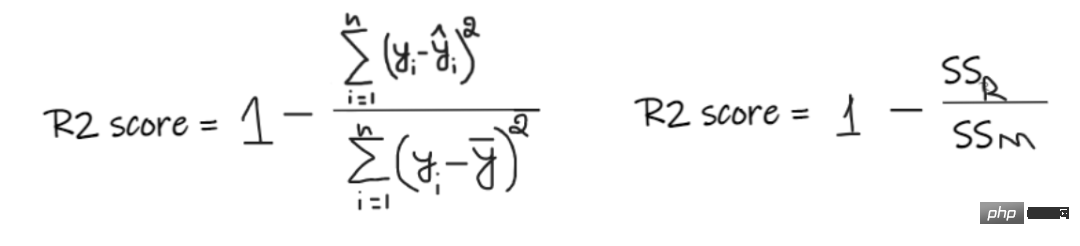
R2 score 給出的值介於 0 到 1 之間,可以針對任何上下文進行解釋。它可以理解為是適合度的好壞。
SSR 是迴歸線的誤差平方和,SSM 是均線誤差的平方和。我們將迴歸線與平均線進行比較。
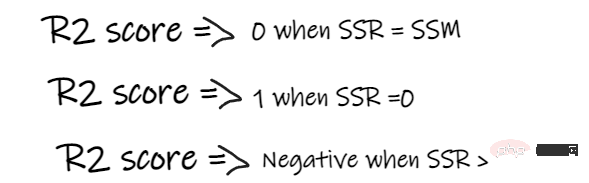
如果我們模型的R2 得分為0.8,這意味著可以說模型能夠解釋80% 的輸出變異數。也就是說,80%的薪資變動可以用輸入(工作年資)來解釋,但剩下的20%是未知的。
如果我們的模型有2個特徵,工作年資和麵試分數,那麼我們的模型能夠使用這兩個輸入特徵來解釋80%的薪資變化。
隨著輸入特徵數量的增加,R2會趨於相應的增加或保持不變,但永遠不會下降,即使輸入特徵對我們的模型不重要(例如,將面試當天的氣溫添加到我們的範例中,R2是不會下降的即使溫度對輸出不重要)。
上式中R2為R2,n為觀測數(行),p為獨立特徵數。 Adjusted R2解決了R2的問題。
當我們加入對我們的模型不那麼重要的特性時,例如添加溫度來預測工資.....

當加入對模型很重要的特性時,例如加入面試分數來預測薪資…

以上是機器學習迴歸模型相關重要知識點總結的詳細內容。更多資訊請關注PHP中文網其他相關文章!




