深入了解Vue中的雙端diff 演算法

diff 演算法是渲染器中最複雜的部分，這篇文章帶大家了解一下Vue中的雙端diff 演算法，希望對大家有幫助！

Vue 和 React 都是基於 vdom 的前端框架，元件渲染會回傳 vdom，渲染器再把 vdom 透過增刪改的 api 同步到 dom。 （學習影片分享：vuejs影片教學）

當再次渲染時，會產生新的vdom，渲染器會對比兩棵vdom 樹，對有差異的部分透過增刪改的api 更新到dom。

這裡比較兩棵 vdom 樹，找到有差異的部分的演算法，就叫做 diff 演算法。

diff 演算法是渲染器中最複雜的部分，也是面試的熱門議題。今天我們就透過 Vue 的 diff 演算法來探究下 diff 演算法吧。

diff 演算法

我們知道，兩棵樹做diff，複雜度是O(n^3) 的，因為每個節點都要去和另一棵樹的全部節點對比一次，這就是n 了，如果找到有變化的節點，執行插入、刪除、修改也是n 的複雜度。所有的節點都是這樣，再乘以 n，所以是 O(n * n * n) 的複雜度。

這樣的複雜度對於前端框架來說是不可接受的，這意味著1000 個節點，渲染一次就要處理1000 * 1000 * 1000，總共10 億次。

所以前端框架的 diff 約定了兩種處理原則：只做同層的對比，type 變了就不再對比子節點。

因為 dom 節點做跨層級移動的情況還是比較少的，一般情況下都是同一層級的 dom 的增刪改。

這樣只要遍歷一遍，對比一下 type 就行了，是 O(n) 的複雜度，而且 type 變了就不再對比子節點，能省下一大片節點的遍歷。另外，因為 vdom 中記錄了關聯的 dom 節點，執行 dom 的增刪改也不需要遍歷，是 O(1)的，整體的 diff 演算法複雜度就是 O(n) 的複雜度。

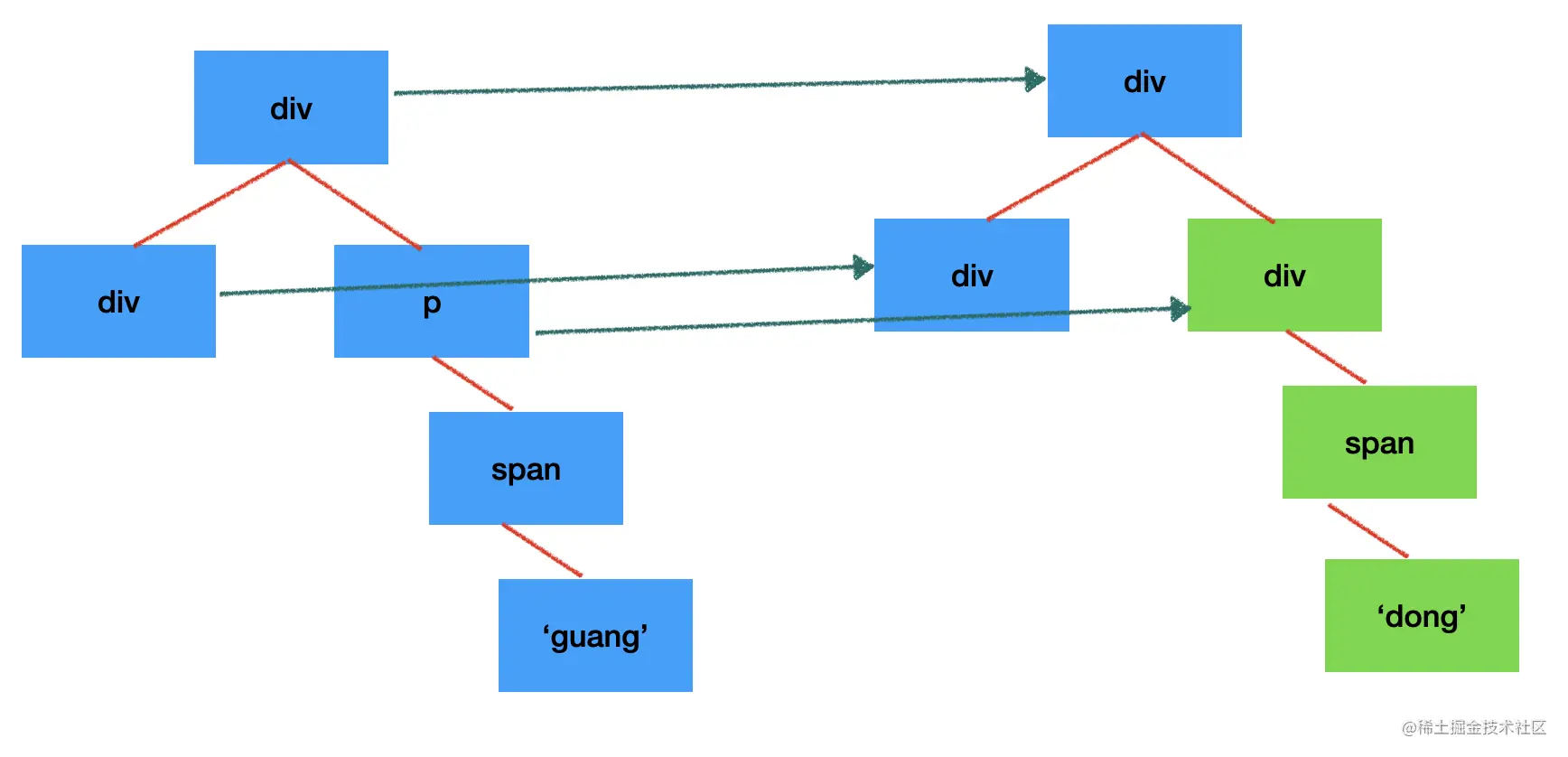
1000 節點渲染一次最多對比 1000 次，這樣的複雜度就是可接受的範圍了。

但是這樣的演算法雖然複雜度低了，卻還是有問題的。

例如一組節點，假設有 5 個，類型是 ABCDE，下次渲染出來的是 EABCD，這時候逐一對比，發現 type  不一樣，就會重新渲染這 5 個節點。

而且根據 type 不同就不再對比子節點的原則，如果這些節點有子節點，也會重新渲染。

dom 操作是比較慢的，這樣雖然 diff 的演算法複雜度是低了，重新渲染的效能也不高。

所以，diff 演算法除了考慮本身的時間複雜度之外，還要考慮一個因素：dom 操作的次數。

上面那個範例的 ABCDE 變成 EABCD，很明顯只需要移動 E 就行了，根本不用建立新元素。

但是怎麼比較出是同個節點發生了移動呢？

判斷 type 麼？那不行，同 type 的節點可能很多，區分不出來的。

最好每個節點都是有唯一的識別。

所以當渲染一組節點的時候，前端框架會讓開發者指定 key，透過 key 來判斷是不是有點節點只是發生了移動，從而直接復用。

這樣，diff 演算法處理一組節點的比較的時候，就要根據 key 來再做一次演算法的最佳化。

我們會把基於 key 的兩組節點的 diff 演算法叫做多節點 diff 演算法，它是整個 vdom 的 diff 演算法的一部分。

接下來我們來學習多節點diff 演算法：

簡單diff

假設渲染ABCD 一組節點，再次渲染是DCAB，這時候怎麼處理呢？

多節點 diff 演算法的目的是為了盡量重複使用節點，透過移動節點代替創建。

所以新 vnode 數組的每個節點我們都要找下在舊 vnode 數組中有沒有對應 key 的，有的話就移動到新的位置，沒有的話再創建新的。

也就是這樣的：

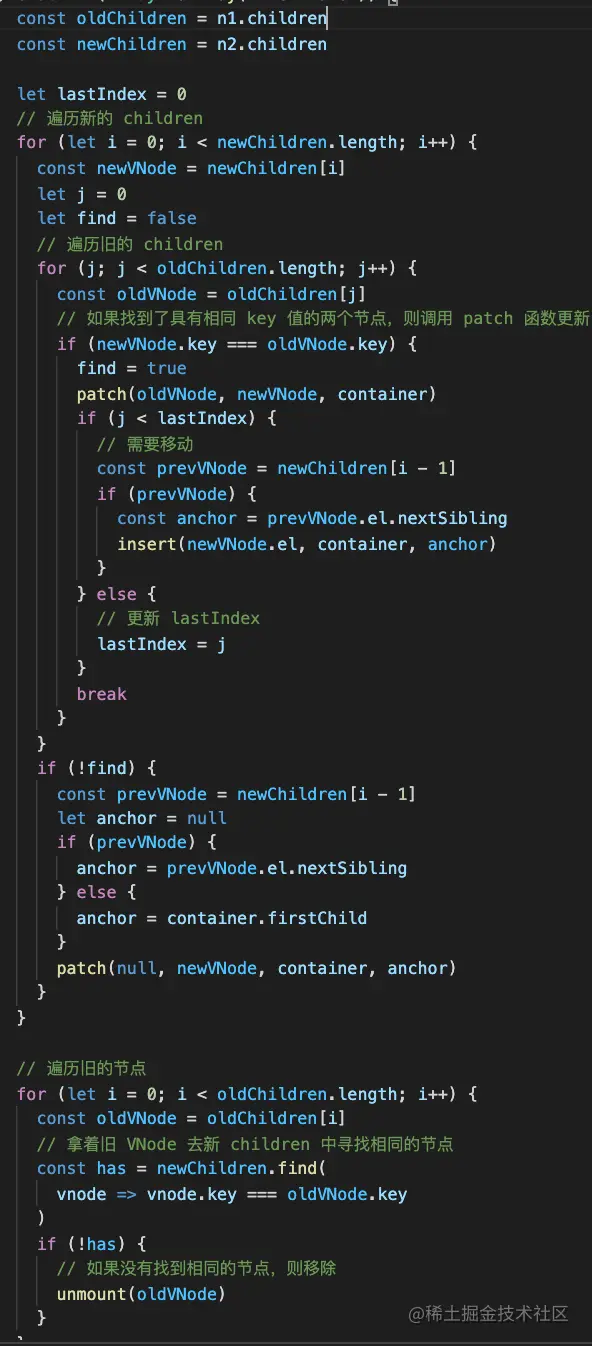
const oldChildren = n1.children
const newChildren = n2.children

let lastIndex = 0
// 遍历新的 children
for (let i = 0; i < newChildren.length; i++) {
    const newVNode = newChildren[i]
    let j = 0
    let find = false
    // 遍历旧的 children
    for (j; j < oldChildren.length; j++) {
      const oldVNode = oldChildren[j]
      // 如果找到了具有相同 key 值的两个节点，则调用 patch 函数更新
      if (newVNode.key === oldVNode.key) {
        find = true
        patch(oldVNode, newVNode, container)
        
        处理移动...
        
        break //跳出循环，处理下一个节点
      }
   }
   // 没有找到就是新增了
   if (!find) {
      const prevVNode = newChildren[i - 1]
      let anchor = null
      if (prevVNode) {
        anchor = prevVNode.el.nextSibling
      } else {
        anchor = container.firstChild
      }
      patch(null, newVNode, container, anchor)
   }
}

這裡的 patch 函數的作用是更新節點的屬性，重新設定事件監聽器。如果沒有對應的舊節點的話，就是插入節點，需要傳入一個它之後的節點作為錨點 anchor。

我們遍歷處理新的 vnode：

先從舊的 vnode 陣列中找出對應的節點，如果找到了就代表可以重複使用，接下來只要移動就好了。

如果沒找到，那就執行插入，錨點是上一個節點的 nextSibling。

那如果找到了可复用的节点之后，那移动到哪里呢？

其实新的 vnode 数组中记录的顺序就是目标的顺序。所以把对应的节点按照新 vnode 数组的顺序来移动就好了。

const prevVNode = newChildren[i - 1]
if (prevVNode) {
    const anchor = prevVNode.el.nextSibling
    insert(newVNode.el, container, anchor)
}

要插入到 i 的位置，那就要取 i-1 位置的节点的 nextSibling 做为锚点来插入当前节点。

但是并不是所有的节点都需要移动，比如处理到第二个新的 vnode，发现它在旧的 vnode 数组中的下标为 4，说明本来就是在后面了，那就不需要移动了。反之，如果是 vnode 查找到的对应的旧的 vnode 在当前 index 之前才需要移动。

也就是这样：

let j = 0
let find = false
// 遍历旧的 children
for (j; j < oldChildren.length; j++) {
    const oldVNode = oldChildren[j]
    // 如果找到了具有相同 key 值的两个节点，则调用 patch 函数更新之
    if (newVNode.key === oldVNode.key) {
        find = true
        patch(oldVNode, newVNode, container)

        if (j < lastIndex) { // 旧的 vnode 数组的下标在上一个 index 之前，需要移动
          const prevVNode = newChildren[i - 1]
          if (prevVNode) {
            const anchor = prevVNode.el.nextSibling
            insert(newVNode.el, container, anchor)
          }
        } else {// 不需要移动
          // 更新 lastIndex
          lastIndex = j
        }
        break
    }
}

查找新的 vnode 在旧的 vnode 数组中的下标，如果找到了的话，说明对应的 dom 就是可以复用的，先 patch 一下，然后移动。

移动的话判断下下标是否在 lastIndex 之后，如果本来就在后面，那就不用移动，更新下 lastIndex 就行。

如果下标在 lastIndex 之前，说明需要移动，移动到的位置前面分析过了，就是就是新 vnode 数组 i-1 的后面。

这样，我们就完成了 dom 节点的复用和移动。

新的 vnode 数组全部处理完后，旧的 vnode 数组可能还剩下一些不再需要的，那就删除它们：

// 遍历旧的节点
for (let i = 0; i < oldChildren.length; i++) {
    const oldVNode = oldChildren[i]
    // 拿着旧 VNode 去新 children 中寻找相同的节点
    const has = newChildren.find(
      vnode => vnode.key === oldVNode.key
    )
    if (!has) {
      // 如果没有找到相同的节点，则移除
      unmount(oldVNode)
    }
}

这样，我们就完成了两组 vnode 的 diff 和对应 dom 的增删改。

小结一下：

diff 算法的目的是根据 key 复用 dom 节点，通过移动节点而不是创建新节点来减少 dom 操作。

对于每个新的 vnode，在旧的 vnode 中根据 key 查找一下，如果没查找到，那就新增 dom 节点，如果查找到了，那就可以复用。

复用的话要不要移动要判断下下标，如果下标在 lastIndex 之后，就不需要移动，因为本来就在后面，反之就需要移动。

最后，把旧的 vnode 中在新 vnode 中没有的节点从 dom 树中删除。

这就是一个完整的 diff 算法的实现。

这个 diff 算法我们是从一端逐个处理的，叫做简单 diff 算法。

简单 diff 算法其实性能不是最好的，比如旧的 vnode 数组是 ABCD，新的 vnode 数组是 DABC，按照简单 diff 算法，A、B、C 都需要移动。

那怎么优化这个算法呢？

从一个方向顺序处理会有这个问题，那从两个方向同时对比呢？

这就是双端 diff 算法：

双端 diff

简单 diff 算法能够实现 dom 节点的复用，但有的时候会做一些没必要的移动。双端 diff 算法解决了这个问题，它是从两端进行对比。

我们需要 4 个指针，分别指向新旧两个 vnode 数组的头尾：

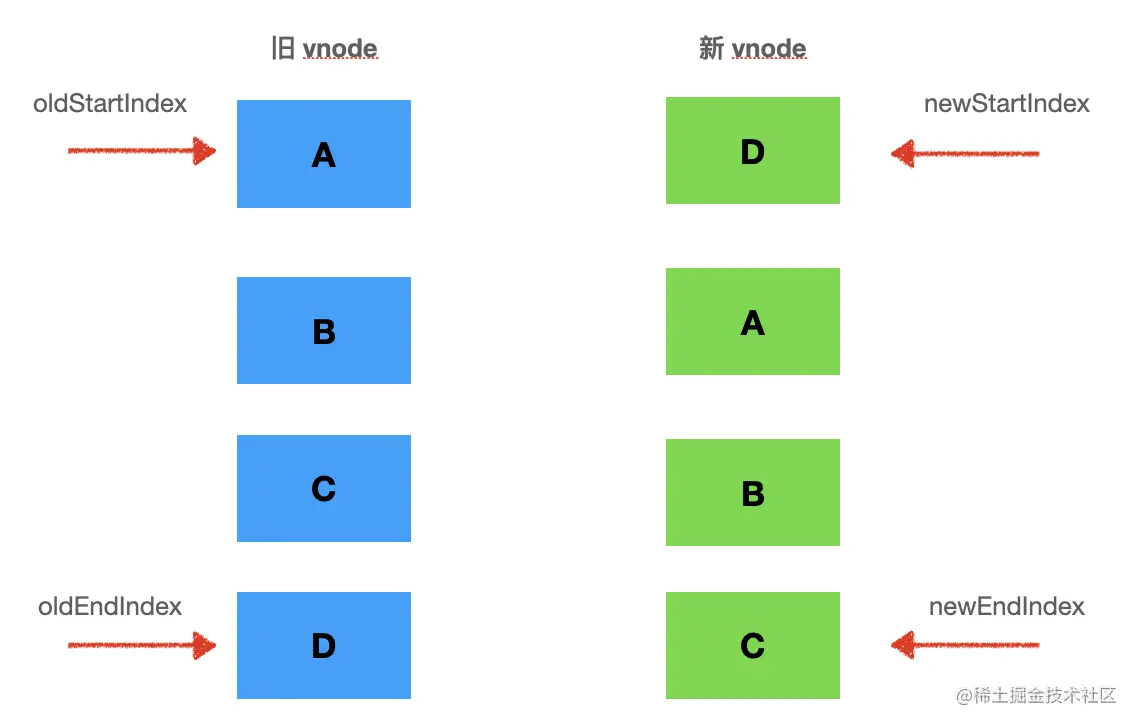
头和尾的指针向中间移动，直到 oldStartIdx <= oldEndIdx 并且 newStartIdx <= newEndIdx，说明就处理完了全部的节点。

每次对比下两个头指针指向的节点、两个尾指针指向的节点，头和尾指向的节点，是不是 key是一样的，也就是可复用的。

如果是可复用的话就直接用，调用 patch 更新一下，如果是头尾这种，还要移动下位置。

也就是这样的：

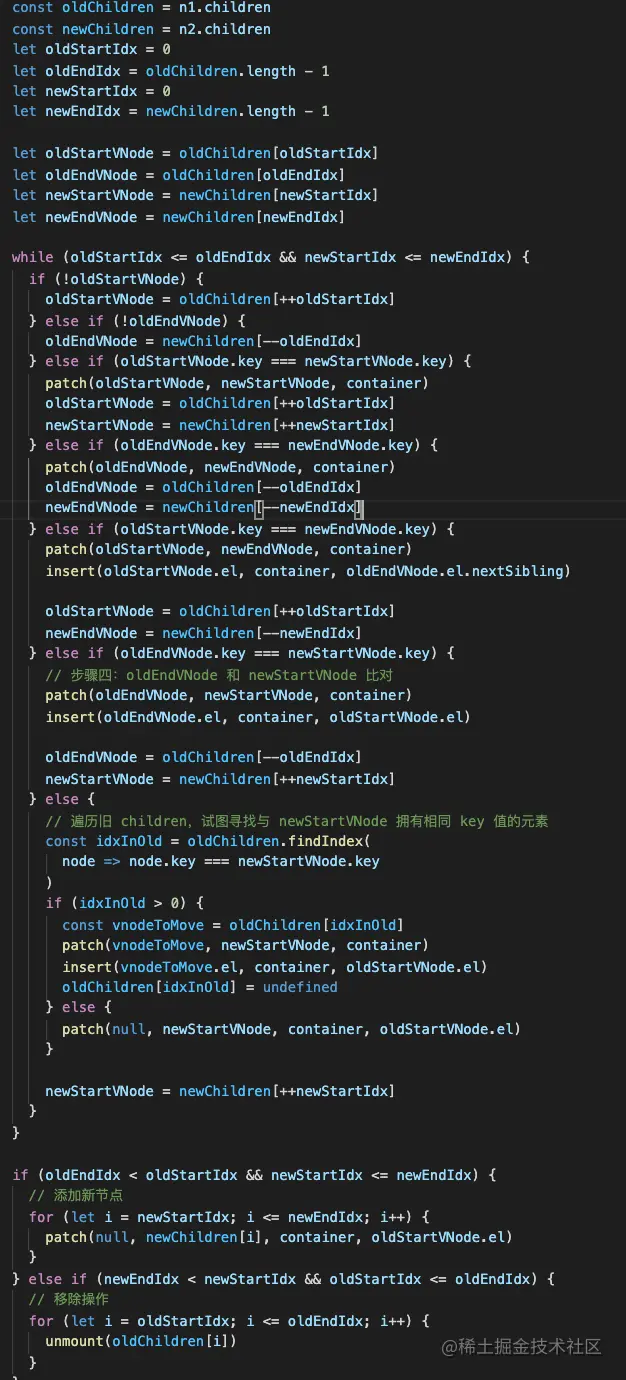
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
  if (oldStartVNode.key === newStartVNode.key) { // 头头
    patch(oldStartVNode, newStartVNode, container)
    oldStartVNode = oldChildren[++oldStartIdx]
    newStartVNode = newChildren[++newStartIdx]
  } else if (oldEndVNode.key === newEndVNode.key) {//尾尾
    patch(oldEndVNode, newEndVNode, container)
    oldEndVNode = oldChildren[--oldEndIdx]
    newEndVNode = newChildren[--newEndIdx]
  } else if (oldStartVNode.key === newEndVNode.key) {//头尾，需要移动
    patch(oldStartVNode, newEndVNode, container)
    insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling)

    oldStartVNode = oldChildren[++oldStartIdx]
    newEndVNode = newChildren[--newEndIdx]
  } else if (oldEndVNode.key === newStartVNode.key) {//尾头，需要移动
    patch(oldEndVNode, newStartVNode, container)
    insert(oldEndVNode.el, container, oldStartVNode.el)

    oldEndVNode = oldChildren[--oldEndIdx]
    newStartVNode = newChildren[++newStartIdx]
  } else {
    
    // 头尾没有找到可复用的节点
  }
}

头头和尾尾的对比比较简单，头尾和尾头的对比还要移动下节点。

比如旧 vnode 的头节点是新的 vnode 的尾节点，那就要把它移动到旧的 vnode 的尾节点的位置。

也就是：

insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling)

插入节点的锚点节点是 oldEndVNode 对应的 dom 节点的 nextSibling。

如果旧 vnode 的尾节点是新 vnode 的头结点，那就要把它移动到旧 vnode 的头结点的位置。

也就是：

insert(oldEndVNode.el, container, oldStartVNode.el)

插入节点的锚点节点是 oldStartVNode 对应的 dom 节点（因为要插在它之前）。

从双端进行对比，能尽可能的减少节点移动的次数。

当然，还要处理下如果双端都没有可复用节点的情况：

如果双端都没有可复用节点，那就在旧节点数组中找，找到了就把它移动过来，并且原位置置为 undefined。没找到的话就插入一个新的节点。

也就是这样：

const idxInOld = oldChildren.findIndex(
  node => node.key === newStartVNode.key
)
if (idxInOld > 0) {
  const vnodeToMove = oldChildren[idxInOld]
  patch(vnodeToMove, newStartVNode, container)
  insert(vnodeToMove.el, container, oldStartVNode.el)
  oldChildren[idxInOld] = undefined
} else {
  patch(null, newStartVNode, container, oldStartVNode.el)
}

因为有了一些 undefined 的节点，所以要加上空节点的处理逻辑：

if (!oldStartVNode) {
    oldStartVNode = oldChildren[++oldStartIdx]
} else if (!oldEndVNode) {
    oldEndVNode = newChildren[--oldEndIdx]
}

这样就完成了节点的复用和移动的逻辑。

那确实没有可复用的节点的那些节点呢？

经过前面的移动之后，剩下的节点都被移动到了中间，如果新 vnode 有剩余，那就批量的新增，如果旧 vnode 有剩余那就批量的删除。

因为前面一个循环的判断条件是 oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx，这样如果 old vnode 多了，最后 newStartIdx 会小于 newEndIdx。如果 new vnode 多了，最后 oldStartIdx 会小于 oldEndIdx。

所以判断条件是这样的：

if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {
  // 添加新节点
  for (let i = newStartIdx; i <= newEndIdx; i++) {
    patch(null, newChildren[i], container, oldStartVNode.el)
  }
} else if (newEndIdx < newStartIdx && oldStartIdx <= oldEndIdx) {
  // 移除操作
  for (let i = oldStartIdx; i <= oldEndIdx; i++) {
    unmount(oldChildren[i])
  }
}

这样就是一个完整的 diff 算法了，包括查找可复用节点和移动节点、新增和删除节点。

而且因为从两侧查找节点，会比简单 diff 算法性能更好一些。

比如 ABCD 到 DABC，简单 diff 算法需要移动 ABC 三个节点，而双端 diff 算法只需要移动 D 一个节点。

小结一下：

双端 diff 是头尾指针向中间移动的同时，对比头头、尾尾、头尾、尾头是否可以复用，如果可以的话就移动对应的 dom 节点。

如果头尾没找到可复用节点就遍历 vnode 数组来查找，然后移动对应下标的节点到头部。

最后还剩下旧的 vnode 就批量删除，剩下新的 vnode 就批量新增。

双端 diff 算法是 Vue2 采用的 diff 算法，性能还不错。

后来，Vue3 又对 diff 算法进行了一次升级，叫做快速 diff 算法。这个后面再讲。

总结

React 和 Vue 都是基于 vdom 的前端框架，组件产生 vdom，渲染器再把 vdom 通过增删改的 dom api 更新到 dom。

当再次渲染出 vdom 时，就要新旧两棵 vdom 树做 diff，只更新变化的 dom 节点。

两棵树的 diff 是 O(n^3) 的，时间复杂度太高，因此前端框架规定了只做同层 diff，还有 type 不一样就认为节点不一样，不再对比子节点。这样时间复杂度一下子就降到了 O(n)。

但是对于多个子字节点的 diff 不能粗暴的删除和新增，要尽量复用已有的节点，也就是通过移动代替新增。

所以多节点的时候，要指定 key，然后 diff 算法根据 key 来查找和复用节点。

简单 diff 算法是依次根据 key 查找旧节点的，移动的话通过 lastIndex 判断，大于它就不用动，小于它才需要移动。剩下的节点再批量删除和新增。

但是简单 diff 算法局限性还是比较大的，有些情况下性能并不好，所以 vue2 用的是双端 diff 算法。

双端 diff 算法是头尾指针向中间移动，分别判断头尾节点是否可以复用，如果没有找到可复用的节点再去遍历查找对应节点的下标，然后移动。全部处理完之后也要对剩下的节点进行批量的新增和删除。

其实 diff 算法最重要的就是找到可复用的节点，然后移动到正确的位置。只不过不同的算法查找顺序不一样。

vue2 是用的双端 diff 的算法，而 vue3 则通过最长递增子序列的算法做了进一步的优化，关于优化后的 diff 算法，我们之后再聊。

【相关视频教程推荐：web前端】

以上是深入了解Vue中的雙端diff 演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章！