這篇文章帶給大家的內容是介紹使用JS如何實現排序和搜尋演算法,有一定的參考價值,有需要的朋友可以參考一下,希望對你有幫助。
在進入正題之前,先準備幾個基礎的函數
(1)交換陣列兩個元素
function swap(arr, sourceIndex, targetIndex) {
let temp = arr[sourceIndex];
arr[sourceIndex] = arr[targetIndex];
arr[targetIndex] = temp;
}(2)快速產生0~N的陣列
function createArr(length) {
return Array.from({length}, (_, i) => i);
}(3)洗牌函數
洗牌函數可快速打亂數組,常見的用法如切換音樂播放順序
function shuffle(arr) {
for (let i = 0; i <h2><strong>二、排序</strong></h2>##常見排序演算法可以分為兩大類:<p></p>,因此也稱為非線性時間比較類別排序
核心:比較任何兩個相鄰的項,如果第一個比第二個大,則交換它們。元素項向上移動至正確的順序,就好像氣泡升至表面一樣,冒泡排序因而得名
#動圖:

注意:第一層遍歷找出剩餘元素的最大值,至指定位置【依序冒泡出最大值】
function bubbleSort(arr) {
const len = arr.length;
for (let i = 0; i arr[j + 1]) { // 比较相邻元素
swap(arr, j, j + 1);
}
}
}
return arr;
}2.2 選擇排序
選擇排序是一種原址比較排序演算法。動圖:
#:第一層遍歷找出剩餘元素最小值的索引,然後交換目前位置和最小值索引值【依序找到最小值】
#程式碼:##function selectionSort(arr) {
const len = arr.length;
let minIndex;
for (let i = 0; i arr[j]) {
minIndex = j; // 寻找最小值对应的索引
}
}
if (minIndex === i) continue;
swap(arr, minIndex, i);
}
return arr;
}
插入排序的比較順序不同於冒泡排序和選擇排序,插入排序的比較順序是當前項目向前比較。
類別定義了一個注意:從第二項開始,依序向前比較,保證目前項先前的序列是順序排列#程式碼:function insertionSort(arr) { const len = arr.length; let current, pointer; for (let i = 1; i = 0 && current <code></code>2.4 歸併排序<strong></strong><code>歸併排序與快速排序相較於上面三種排序演算法在實際中更有可行性(在第四小節我們會透過實踐複雜度來比較這幾種排序演算法)</code><code></code>JavaScript<strong>的</strong>Array登入後複製
sort函數(Array.prototype.sort)用來排序JavaScript陣列。 ECMAScript
Mozilla Firefox使用歸併排序
作為Array.prototype.sort的實現,而Chrome
使用了一個快速排序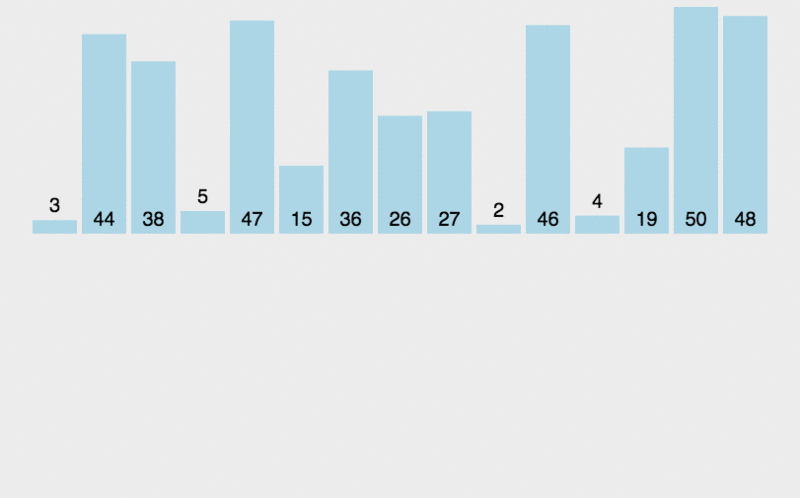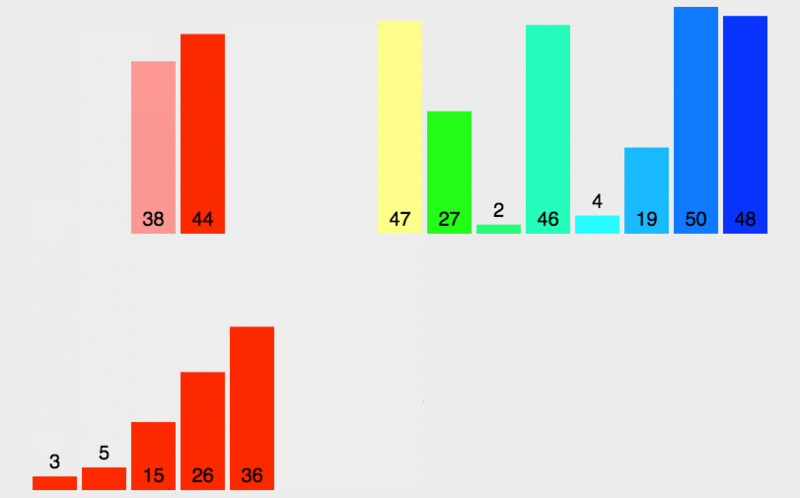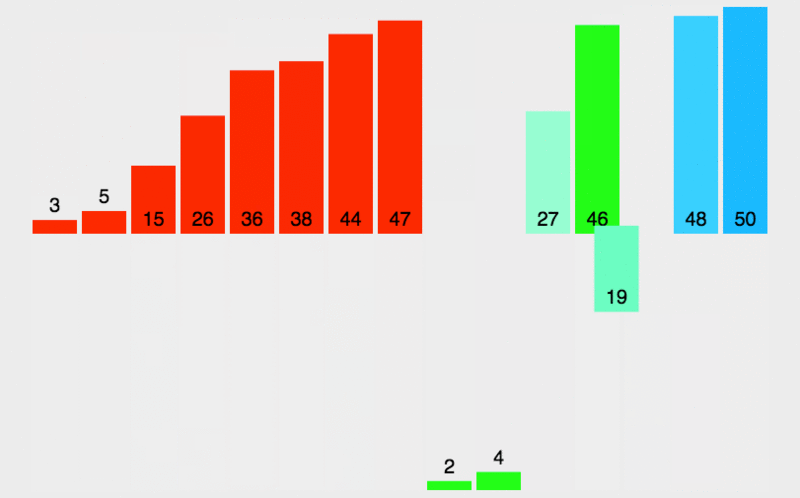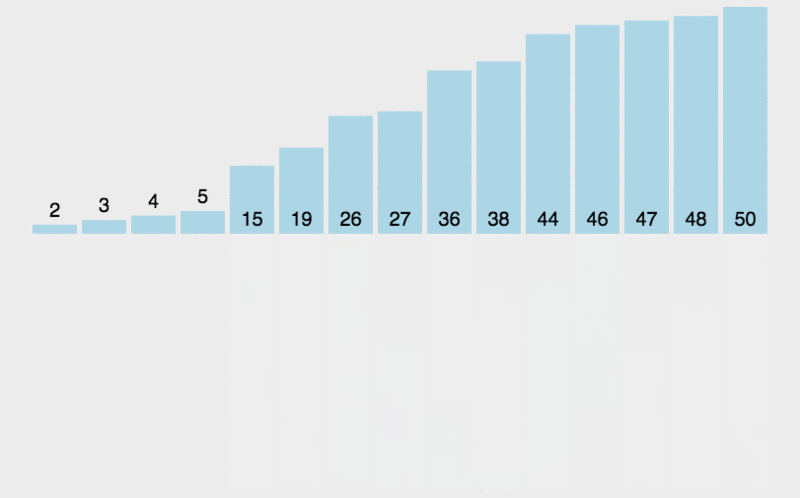 的變體
的變體
注意:递归中最小的左右数组比较为单个元素的数组,因此在较上层多个元素对比时,左右两个数组一定是顺序的
代码:
function mergeSort(arr) {
const len = arr.length;
if (len right[0]) {
ret.push(right.shift());
} else {
ret.push(left.shift());
}
}
while (left.length) {
ret.push(left.shift());
}
while (right.length) {
ret.push(right.shift());
}
return ret;
}快速排序也许是最常用的排序算法了。它的复杂度为O(nlogn),且它的性能通常比其他的复 杂度为O(nlogn)的排序算法要好。和归并排序一样,快速排序也使用分治的方法,将原始数组分为较小的数组
核心:分治算法,以参考值为界限,将比它小的和大的值拆开
动图:
注意:每一次遍历筛选出比基准点小的值
代码:
function quickSort(arr, left = 0, right = arr.length - 1) {
// left和right默认为数组首尾
if (left <h2><strong>三、搜索算法</strong></h2><h3><strong>3.1 顺序搜索</strong></h3><p>顺序或线性搜索是最基本的搜索算法。它的机制是,将每一个数据结构中的元素和我们要找的元素做比较。<strong>顺序搜索是最低效的一种搜索算法。</strong></p><pre class="brush:php;toolbar:false">function findItem(item, arr) {
for (let i = 0; i <h3><strong>3.2 二分搜索</strong></h3><p>二分搜索要求被搜索的数据结构已排序。以下是该算法遵循的步骤:</p><ol>
<li>选择数组的中间值</li>
<li>如果选中值是待搜索值,那么算法执行完毕</li>
<li>如果待搜索值比选中值要小,则返回步骤1在选中值左边的子数组中寻找</li>
<li>如果待搜索值比选中值要大,则返回步骤1在选中值右边的子数组中寻找</li>
</ol><pre class="brush:php;toolbar:false">function binarySearch(item, arr) {
arr = quickSort(arr); // 排序
let low = 0;
let high = arr.length - 1;
let mid;
while (low item) {
high = mid - 1;
} else {
return mid;
}
}
return -1;
}大O表示法用于描述算法的性能和复杂程度。分析算法时,时常遇到一下几类函数
(1)O(1)
function increment(num){
return ++num;
}执行时间和参数无关。因此说,上述函数的复杂度是O(1)(常数)
(2)O(n)
以顺序搜索函数为例,查找元素需要遍历整个数组,直到找到该元素停止。函数执行的总开销取决于数组元素的个数(数组大小),而且也和搜索的值有关。但是函数复杂度取决于最坏的情况:如果数组大小是10,开销就是10;如果数组大小是1000,开销就是1000。这种函数的时间复杂度是O(n),n是(输入)数组的大小
(3)O(n2)
以冒泡排序为例,在未优化的情况下,每次排序均需进行n*n次执行。时间复杂度为O(n2)
时间复杂度O(n)的代码只有一层循环,而O(n2)的代码有双层嵌套循环。如 果算法有三层遍历数组的嵌套循环,它的时间复杂度很可能就是O(n3)
(1)常用数据结构时间复杂度
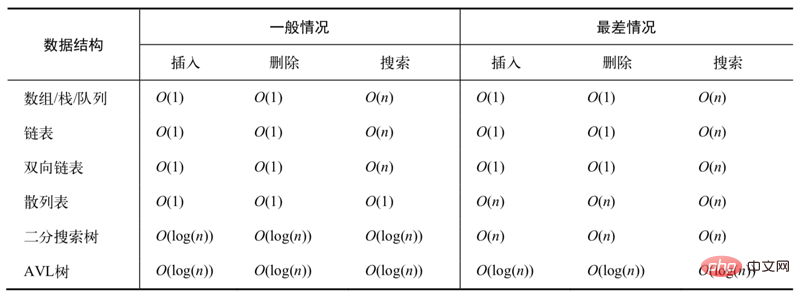
(2)排序算法时间复杂度
相关视频教程推荐:《JavaScript教程》
以上就是本篇文章的全部内容,希望能对大家的学习有所帮助。更多精彩内容大家可以关注php中文网相关教程栏目!!!
以上是JS如何實作排序和搜尋演算法的詳細內容。更多資訊請關注PHP中文網其他相關文章!


