2699。修改圖邊權重
難度:難
主題:圖、堆(優先權隊列)、最短路徑
給你一個無向加權連通圖,其中包含標記為0到n - 1的n個節點,以及一個整數數組edges,其中edges[i] = [ai, bi, wi] 表示節點ai和bi之間有一條邊,權重為wi.
某些邊的權重為-1 (wi= -1),而其他邊的權重為正(wi> 0) .
你的任務是修改所有邊的權重為-1,方法是在[1, 2 * 109範圍內分配正整數值] 使得節點來源與目的地之間的最短距離變成等於整數目標。如果有多次修改使來源和目的地之間的最短距離等於目標,則其中任何一個都將被視為正確。
如果可以使從來源到目的地的最短距離等於目標,則傳回以任意順序包含所有邊(甚至未修改的邊)的數組,如果不可能,則傳回空數組.
注意:不允許修改初始為正權重的邊的權重。
範例1:
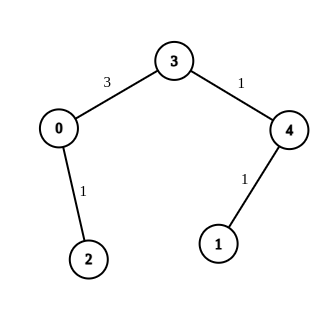
- 輸入:n = 5,邊= [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1] ],來源= 0,目的地= 1,目標= 5
- 輸出:[[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
- 解釋:上圖顯示了對邊緣的可能修改,使得從 0 到 1 的距離等於 5。
範例2:
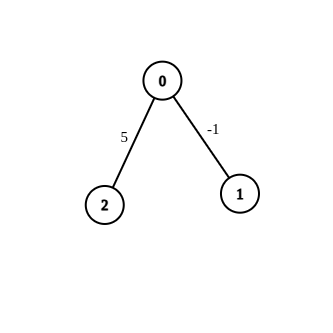
- 輸入:n = 3,邊 = [[0,1,-1],[0,2,5]],來源 = 0,目的地 = 2,目標 = 6
- 輸出:[]
- 解釋:上圖包含初始邊。透過修改權重-1的邊是不可能使從0到2的距離等於6的。因此,傳回一個空數組。
範例 3:
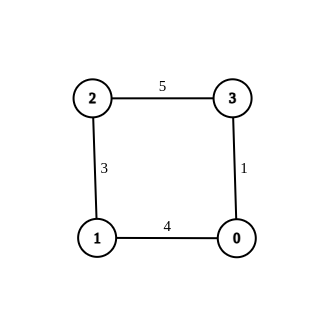
- 輸入:n = 4,邊= [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]],源= 0,目的地= 2,目標= 6
- 輸出:[[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
- 解釋:上圖顯示了修改後的圖,其中從 0 到 2 的最短距離為 6。
約束:
- 1
- 1
- 邊[i].length == 3
- 0 i, bi
- wi= -1 或 1 i 7
- ai!= bi
- 0
- 來源! =目的地
- 1 9
- 圖是連通的,不存在自環或重複邊
提示:
- 首先,檢查是否確實可以使從來源到目的地的最短路徑等於目標。
- 如果在沒有修改邊的情況下從來源到目的地的最短路徑小於目標,則這是不可能的。
- 如果從來源到目的地的最短路徑(包括要修改的邊並為其分配臨時權重 1)大於目標,那麼它也是不可能的。
- 假設我們可以找到一條可修改的邊(u, v),使得從來源到u 的最短路徑長度(dis1) 加上從v 到目的地的最短路徑長度(dis2) 小於目標(dis1) + dis2
- 對於所有其他仍具有權重「-1」的邊,將權重更改為足夠大的數字(目標、目標 + 1 或 200000000 等)。
解:
我們可以將方法分解如下:
方法:
對現有權重進行初步檢查:
- First, we compute the shortest path from source to destination using only the edges with positive weights, ignoring the edges with weight -1.
- If this distance is already greater than target, then it's impossible to modify the -1 edges to achieve the target, so we return an empty array.
Temporary Assignment of Weight 1:
- Next, assign a temporary weight of 1 to all edges with weight -1 and recompute the shortest path.
- If this shortest path is still greater than target, then it's impossible to achieve the target, so we return an empty array.
Modify Specific Edge Weights:
- Iterate through the edges with weight -1 and identify edges that can be adjusted to exactly match the target distance. This is done by adjusting the weight of an edge such that the combined distances of paths leading to and from this edge result in the exact target distance.
- For any remaining -1 edges, assign a large enough weight (e.g., 2 * 10^9) to ensure they don't impact the shortest path.
Return Modified Edges:
- Finally, return the modified list of edges.
Let's implement this solution in PHP:2699. Modify Graph Edge Weights
Explanation:
- The dijkstra function calculates the shortest path from the source to all other nodes.
- We initially compute the shortest path ignoring -1 edges.
- If the path without -1 edges is less than the target, the function returns an empty array, indicating it's impossible to adjust the weights to meet the target.
- Otherwise, we temporarily set all -1 edges to 1 and check if the shortest path exceeds the target.
- If it does, it's again impossible to reach the target, and we return an empty array.
- We then modify the weights of -1 edges strategically to achieve the desired shortest path of exactly target.
This approach efficiently checks and adjusts edge weights, ensuring that the target distance is met if possible.
Contact Links
If you found this series helpful, please consider giving therepositorya star on GitHub or sharing the post on your favorite social networks ?. Your support would mean a lot to me!
If you want more helpful content like this, feel free to follow me:
以上是修改圖邊權重的詳細內容。更多資訊請關注PHP中文網其他相關文章!







