PHP implements Diffie–Hellman key exchange (Diffie–Hellman) algorithm

How does PHP implement the Diffie–Hellman key exchange (Diffie–Hellman) algorithm? This article mainly introduces the principle of Diffie-Hellman key exchange (Diffie-Hellman) algorithm and PHP implementation examples. I hope to be helpful.

Diffie-Hellman is an algorithm that allows both parties to establish a secret key on an insecure public channel. Both parties can later use this secret key for encryption (such as RC4) content.
The principle of Diffie–Hellman algorithm is very simple:

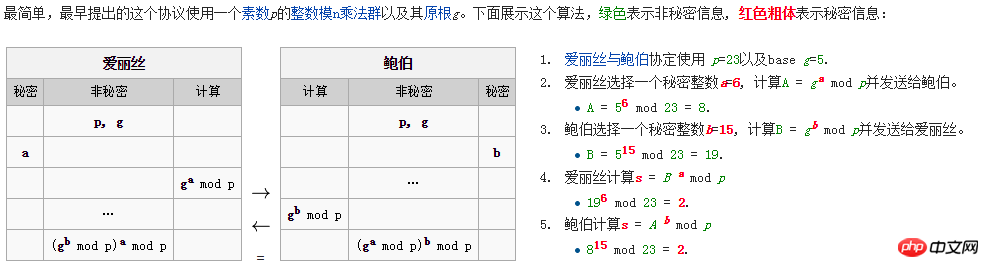
The above principle is easy to prove through mathematical principles(g^ b%p)^a%p = (g^a%p)^b%p, so they get the same key.
Except for a, b and the final public key, which are secret, the others can be transmitted on the public channel. In actual applications, p is very large (more than 300 bits), and g usually takes 2 or 5. Then it is almost impossible to calculate a from p, g and g^a%p (discrete math problem).

Many languages have implemented this algorithm, take Crypt_DiffieHellman in the PHP package as an example:

generateKeys()->getPublicKey(); $bob = new Crypt_DiffieHellman($p, $g, 14); $bob_pubKey = $bob->generateKeys()->getPublicKey(); $alice_computeKey = $alice->computeSecretKey($bob_pubKey)->getSharedSecretKey(); $bob_computeKey = $bob->computeSecretKey($alice_pubKey)->getSharedSecretKey(); echo "{$alice_pubKey}-{$bob_pubKey}-{$alice_computeKey}-{$bob_computeKey}"; //78-534-117-117

Related recommendations:

#php Algorithm to split array without array_chunk()_PHP tutorial

##php Algorithm to print out The picture below

PHP method to solve session deadlock_PHP tutorial

The above is the detailed content of PHP implements Diffie–Hellman key exchange (Diffie–Hellman) algorithm. For more information, please follow other related articles on the PHP Chinese website!