Regresi kuantil untuk ramalan kebarangkalian siri masa

Jangan ubah maksud kandungan asal, perhalusi kandungan, tulis semula kandungan, dan jangan teruskan menulis. "Regression kuantil memenuhi keperluan ini, menyediakan selang ramalan dengan peluang yang dikira. Ia adalah teknik statistik yang digunakan untuk memodelkan hubungan antara pembolehubah peramal dan pembolehubah tindak balas, terutamanya apabila taburan bersyarat pembolehubah tindak balas adalah menarik Apabila. Tidak seperti regresi tradisional kaedah, regresi kuantil memfokuskan pada menganggar magnitud bersyarat pembolehubah tindak balas dan bukannya min bersyarat ”

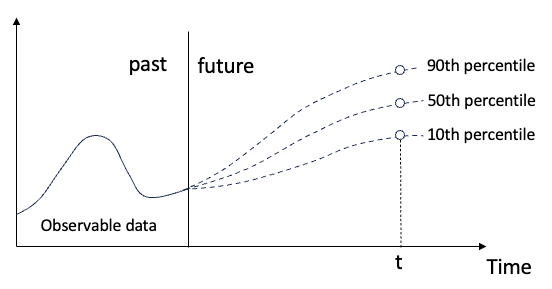Rajah (A): Regresi kuantil

Regresi kuantil ialah kaedah regresi hubungan linear antara set regressor X dan kuantiti pembolehubah yang dijelaskan Y.

Model regresi sedia ada sebenarnya adalah kaedah mengkaji hubungan antara pembolehubah yang dijelaskan dan pembolehubah penjelasan. Mereka memberi tumpuan kepada hubungan antara pembolehubah penjelasan dan pembolehubah yang dijelaskan dan taburan ralat mereka regresi median dan regresi kuantil adalah dua model regresi biasa. Mereka pertama kali dicadangkan menurut Koenker dan Bassett (1978).

Pengiraan penganggar regresi kuasa dua terkecil biasa adalah berdasarkan meminimumkan jumlah baki kuasa dua. Pengiraan penganggar regresi kuantil juga berdasarkan meminimumkan baki nilai mutlak dalam bentuk simetri. Antaranya, operasi regresi median ialah penganggar sisihan mutlak terkecil (LAD, penganggar sisihan mutlak terkecil).

Kelebihan Regresi Kuantil

Jelaskan gambaran penuh taburan bersyarat bagi pembolehubah yang dijelaskan Ia bukan sahaja menganalisis jangkaan bersyarat (min) pembolehubah yang dijelaskan, tetapi juga menganalisis bagaimana pembolehubah penjelasan mempengaruhi median dan kuantil. pembolehubah dijelaskan. Anggaran pekali regresi pada kuantil yang berbeza selalunya berbeza, iaitu pembolehubah penjelasan mempunyai kesan yang berbeza pada kuantil yang berbeza Oleh itu, kesan yang berbeza bagi kuantiti yang berbeza bagi pembolehubah penjelasan akan mempunyai kesan yang berbeza terhadap pembolehubah yang dijelaskan.

Berbanding dengan kaedah pendaraban terkecil, kaedah anggaran untuk regresi median adalah lebih teguh kepada outlier, dan regresi kuantil tidak memerlukan andaian yang kukuh pada istilah ralat, jadi untuk bukan normal Taburan keadaan dan pekali regresi median adalah lebih sihat. Pada masa yang sama, anggaran kuantiti sistem regresi kuantil menjadi lebih mantap.

Apakah kelebihan regresi kuantil berbanding simulasi Monte Carlo? Pertama, regresi kuantil menganggarkan secara langsung magnitud bersyarat pembolehubah tindak balas yang diberikan peramal. Ini bermakna, daripada menghasilkan sejumlah besar hasil yang mungkin seperti simulasi Monte Carlo, ia memberikan anggaran magnitud khusus taburan pembolehubah tindak balas. Ini amat berguna untuk memahami tahap ketidakpastian ramalan yang berbeza, seperti kuintil, kuartil atau magnitud melampau. Kedua, regresi kuantil menyediakan kaedah anggaran ketidakpastian ramalan berasaskan model yang menggunakan data pemerhatian untuk menganggar hubungan antara pembolehubah dan membuat ramalan berdasarkan hubungan ini. Sebaliknya, simulasi Monte Carlo bergantung pada menentukan taburan kebarangkalian untuk pembolehubah input dan menjana keputusan berdasarkan persampelan rawak.

NeuralProphet menyediakan dua teknik statistik: (1) regresi kuantil dan (2) regresi kuantil konformal. Teknik ramalan kuantil konformal menambah proses penentukuran untuk melakukan regresi kuantil. Dalam artikel ini, kami akan menggunakan modul regresi kuantil Nabi Neural untuk membuat ramalan regresi kuantil. Modul ini menambah proses penentukuran untuk memastikan keputusan ramalan adalah konsisten dengan pengagihan data yang diperhatikan. Kami akan menggunakan modul regresi kuantil Nabi Neural dalam bab ini.

Keperluan alam sekitar

Pasang NeuralProphet.

!pip install neuralprophet!pip uninstall numpy!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5

%matplotlib inlinefrom matplotlib import pyplot as pltimport pandas as pdimport numpy as npimport loggingimport warningslogging.getLogger('prophet').setLevel(logging.ERROR)warnings.filterwarnings("ignore")

Data basikal kongsi. Set data ialah set data berbilang variasi yang mengandungi permintaan sewaan harian serta medan cuaca lain seperti suhu atau kelajuan angin.

data = pd.read_csv('/bike_sharing_daily.csv')data.tail()

Gambar (B): Basikal kongsiPlot bilangan basikal kongsi. Kami melihat bahawa permintaan meningkat pada tahun kedua dan mengikut corak bermusim.

# convert string to datetime64data["ds"] = pd.to_datetime(data["dteday"])# create line plot of sales dataplt.plot(data['ds'], data["cnt"])plt.xlabel("date")plt.ylabel("Count")plt.show()

Rajah (C): Permintaan harian untuk sewa basikal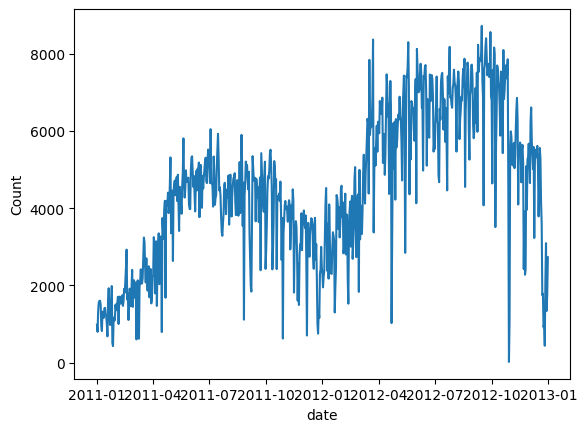 Buat penyediaan data paling asas untuk pemodelan. NeuralProphet memerlukan nama lajur ds dan y, yang sama seperti Nabi.

df = data[['ds','cnt']]df.columns = ['ds','y']

构建分位数回归模型

直接在 NeuralProphet 中构建分位数回归。假设我们需要第 5、10、50、90 和 95 个量级的值。我们指定 quantile_list = [0.05,0.1,0.5,0.9,0.95]，并打开参数 quantiles = quantile_list。

from neuralprophet import NeuralProphet, set_log_levelquantile_list=[0.05,0.1,0.5,0.9,0.95 ]# Model and predictionm = NeuralProphet(quantiles=quantile_list,yearly_seasnotallow=True,weekly_seasnotallow=True,daily_seasnotallow=False)m = m.add_country_holidays("US")m.set_plotting_backend("matplotlib")# Use matplotlibdf_train, df_test = m.split_df(df, valid_p=0.2)metrics = m.fit(df_train, validation_df=df_test, progress="bar")metrics.tail()

分位数回归预测

我们将使用 .make_future_dataframe()为预测创建新数据帧，NeuralProphet 是基于 Prophet 的。参数 n_historic_predictions 为 100，只包含过去的 100 个数据点。如果设置为 True，则包括整个历史数据。我们设置 period=50 来预测未来 50 个数据点。

future = m.make_future_dataframe(df, periods=50, n_historic_predictinotallow=100) #, n_historic_predictinotallow=1)# Perform prediction with the trained modelsforecast = m.predict(df=future)forecast.tail(60)

预测结果存储在数据框架 predict 中。

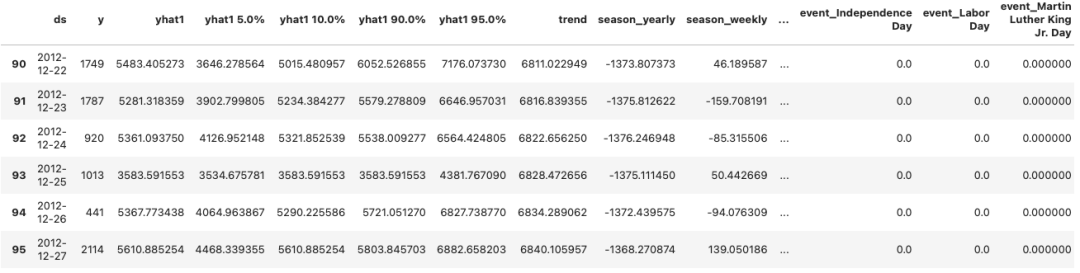图 (D)：预测

上述数据框架包含了绘制地图所需的所有数据元素。

m.plot(forecast, plotting_backend="plotly-static"#plotting_backend = "matplotlib")

预测区间是由分位数值提供的！

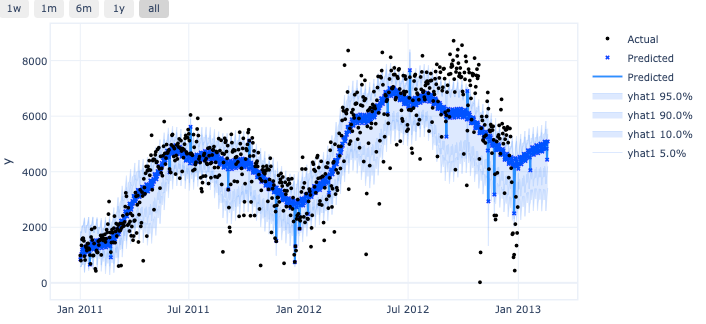图 (E)：分位数预测

预测区间和置信区间的区别

预测区间和置信区间在流行趋势中很有帮助，因为它们可以量化不确定性。它们的目标、计算方法和应用是不同的。下面我将用回归来解释两者的区别。在图(F)中，我在左边画出了线性回归，在右边画出了分位数回归。

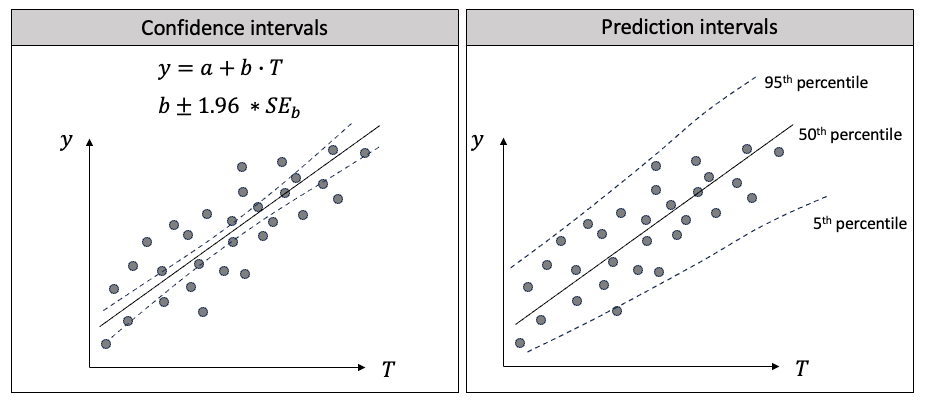图(F)：置信区间与预测区间的区别

首先，它们的目标不同：

• 线性回归的主要目标是找到一条线，使预测值尽可能接近给定自变量值时因变量的条件均值。
• 分位数回归旨在提供未来观测值的范围，在一定的置信度下。它估计自变量与因变量条件分布的不同量化值之间的关系。

其次，它们的计算方法不同：

• 在线性回归中，置信区间是对自变量系数的区间估计，通常使用普通最小二乘法 (OLS) 找出数据点到直线的最小总距离。系数的变化会影响预测的条件均值 Y。
• 在分位数回归中，你可以选择依赖变量的不同量级来估计回归系数，通常是最小化绝对偏差的加权和，而不是使用OLS方法。

第三，它们的应用不同：

• 在线性回归中，预测的条件均值有 95% 的置信区间。置信区间较窄，因为它是条件平均值，而不是整个范围。
• 在分位数回归中，预测值有 95% 的概率落在预测区间的范围内。

写在最后

本文介绍了分位数回归预测区间的概念，以及如何利用 NeuralProphet 生成预测区间。我们还强调了预测区间和置信区间之间的差异，这在商业应用中经常引起混淆。后面将继续探讨另一项重要的技术，即复合分位数回归（CQR），用于预测不确定性。