
Sebelum kita memahami prinsip kerja Model Kebarangkalian Penyebaran Denoising (DDPM) secara terperinci, mari kita fahami dahulu beberapa perkembangan kecerdasan buatan generatif, yang juga merupakan salah satu penyelidikan asas DDPM.

VAE menggunakan pengekod, ruang terpendam kemungkinan dan penyahkod. Semasa latihan, pengekod meramalkan min dan varians setiap imej dan sampel nilai ini daripada taburan Gaussian. Hasil pensampelan dihantar ke penyahkod, yang menukar imej input ke dalam bentuk yang serupa dengan imej output. KL divergence digunakan untuk mengira kerugian. Kelebihan ketara VAE ialah keupayaannya untuk menghasilkan imej yang pelbagai. Dalam peringkat persampelan, seseorang boleh membuat sampel terus daripada taburan Gaussian dan menjana imej baharu melalui penyahkod.
Hanya satu tahun selepas pengekod auto variasi (VAE), sebuah keluarga model generatif yang inovatif muncul - rangkaian musuh generatif (GAN), menandakan kelas model generatif baharu Permulaan model, dicirikan oleh kerjasama dua rangkaian saraf: penjana dan diskriminator, melibatkan proses latihan lawan. Matlamat penjana adalah untuk menjana data sebenar, seperti imej, daripada hingar rawak, manakala diskriminator berusaha untuk membezakan data sebenar daripada data yang dijana. Sepanjang fasa latihan, penjana dan diskriminasi terus meningkatkan keupayaan mereka melalui proses pembelajaran yang kompetitif. Penjana menjana data yang semakin meyakinkan, dengan itu menjadi lebih pintar daripada diskriminator, yang seterusnya meningkatkan keupayaannya untuk membezakan antara sampel sebenar dan sampel yang dijana. Saling bermusuhan ini memuncak dalam penjana menghasilkan data yang realistik dan berkualiti tinggi. Dalam peringkat persampelan, selepas latihan GAN, penjana menjana sampel baharu dengan memasukkan bunyi rawak. Ia menukar bunyi ini kepada data yang secara amnya mencerminkan contoh sebenar.
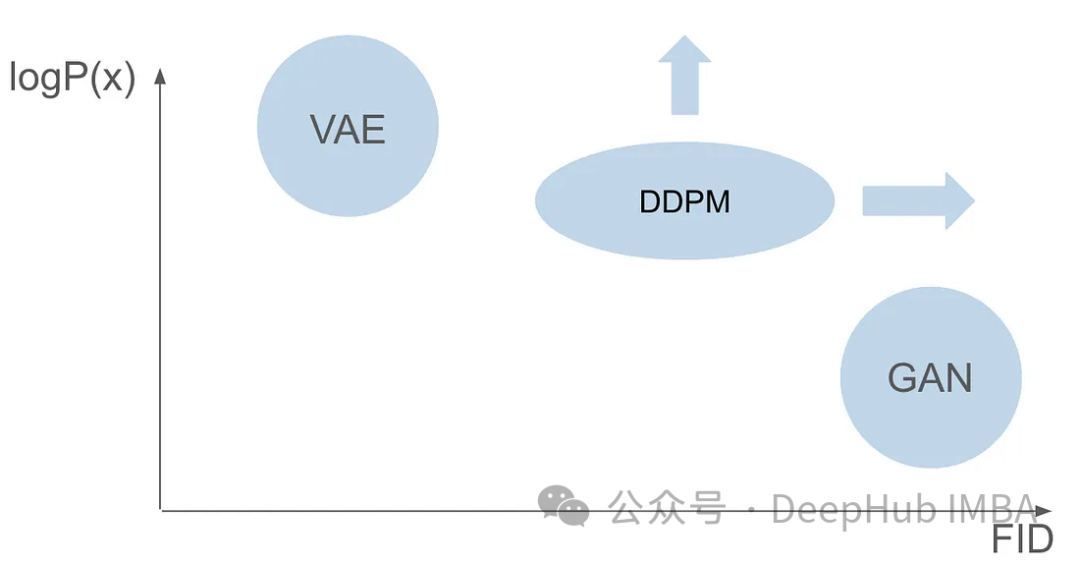
Walaupun GAN dan VAE mempunyai kelebihan tersendiri dalam penjanaan imej, kedua-duanya mempunyai beberapa masalah. GAN boleh menjana imej realistik yang hampir serupa dengan imej dalam set latihan, tetapi hasil yang dihasilkannya tidak mempunyai kepelbagaian. VAE boleh mencipta pelbagai imej, tetapi cenderung menghasilkan imej kabur. Walau bagaimanapun, tidak ada kejayaan dalam menggabungkan kedua-dua keupayaan ini untuk mencipta imej yang sangat realistik dan pelbagai. Cabaran ini merupakan halangan penting bagi penyelidik dan perlu ditangani. Oleh itu, salah satu hala tuju penyelidikan masa hadapan adalah untuk meneroka cara menggabungkan kelebihan GAN dan VAE untuk mencapai penjanaan imej yang sangat realistik dan pelbagai. Ini akan membawa satu kejayaan besar dalam bidang penjanaan imej dan digunakan secara meluas dalam pelbagai bidang.
Enam tahun selepas kertas GAN diterbitkan, dan tujuh tahun selepas kertas VAE diterbitkan, model pecah tanah muncul, iaitu Denoising Diffusion Probabilistic Model (DDPM). DDPM menggabungkan kelebihan kedua-dua medan untuk mencipta imej yang pelbagai dan realistik.
Artikel ini akan meneroka kerumitan DDPM secara terperinci, termasuk proses latihan, proses ke hadapan dan belakang serta kaedah pensampelan. Kami akan menggunakan PyTorch untuk membina dan melatih DDPM dari awal, membimbing pembaca melalui keseluruhan proses.
Diandaikan bahawa anda sudah biasa dengan asas pembelajaran mendalam dan mempunyai asas yang kukuh dalam penglihatan komputer yang mendalam. Kami tidak akan menerangkan secara terperinci tentang konsep asas ini, sebaliknya bertujuan untuk menghasilkan imej yang boleh dipercayai dalam kesahihannya.
Denoising Diffusion Probabilistic Model (DDPM) ialah kaedah termaju dalam bidang model generatif. Berbanding dengan model tradisional yang bergantung pada fungsi kemungkinan eksplisit, DDPM beroperasi melalui proses penyebaran denoising berulang. Proses ini melibatkan penambahan bunyi secara beransur-ansur pada imej dan cuba untuk mengalih keluar bunyi tersebut. Teori asas adalah berdasarkan idea untuk menukar pengedaran mudah (seperti pengedaran Gaussian) kepada pengedaran data imej yang kompleks dan ekspresif melalui satu siri langkah penyebaran. Dalam erti kata lain, dengan memindahkan sampel daripada pengedaran imej asal kepada pengedaran Gaussian, kita boleh membina model untuk membalikkan proses ini. Ini membolehkan kami bermula daripada pengedaran Gaussian sepenuhnya dan menjana imej baharu dengan ciri pengedaran imej, sekali gus mencapai penjanaan imej yang cekap.
Latihan DDPM terdiri daripada dua langkah asas: proses ke hadapan yang menghasilkan imej bising yang tetap dan tidak boleh dipelajari, dan proses terbalik seterusnya. Matlamat utama proses songsang adalah untuk mengecilkan imej menggunakan model pembelajaran mesin khusus.
Proses ke hadapan ialah langkah tetap dan tidak boleh dipelajari, tetapi ia memerlukan beberapa tetapan yang telah ditetapkan. Sebelum kita mendalami tetapan, mari kita fahami dahulu cara ia berfungsi.
Konsep teras proses ini adalah bermula dengan imej yang jelas. Pada saiz langkah tertentu, dilambangkan dengan "T", sejumlah kecil hingar diperkenalkan secara beransur-ansur berikutan taburan Gaussian.

Seperti yang anda lihat daripada imej, bunyi semakin meningkat pada setiap langkah, mari kita mendalami perwakilan matematik bunyi ini.
Bunyi adalah sampel daripada taburan Gaussian. Untuk memperkenalkan sedikit bunyi pada setiap langkah, kami menggunakan rantai Markov. Untuk menjana imej cap masa semasa, kami hanya memerlukan imej cap masa terakhir. Konsep rantai Markov adalah kunci di sini dan akan menjadi penting kepada butiran matematik yang berikut.
Rantai Markov ialah proses stokastik di mana kebarangkalian peralihan kepada mana-mana keadaan tertentu bergantung hanya pada keadaan semasa dan masa berlalu, bukan pada urutan peristiwa sebelumnya. Ciri ini memudahkan pemodelan proses penambahan hingar, menjadikannya lebih mudah untuk menganalisis secara matematik.
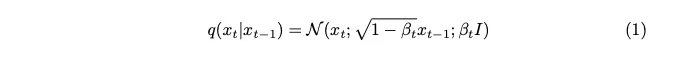
Parameter varians yang dinyatakan sebagai beta sengaja ditetapkan kepada nilai yang sangat kecil untuk memperkenalkan hanya jumlah minimum hingar pada setiap langkah.
Parameter langkah "T" menentukan saiz langkah yang diperlukan untuk menghasilkan imej yang bising sepenuhnya. Dalam artikel ini, parameter ini ditetapkan kepada 1000, yang mungkin kelihatan besar. Adakah kita benar-benar perlu mencipta 1000 imej bising untuk setiap imej asal dalam set data Aspek rantaian Markov terbukti membantu menyelesaikan masalah ini. Memandangkan kami hanya memerlukan imej daripada langkah sebelumnya untuk meramalkan langkah seterusnya, dan hingar yang ditambahkan pada setiap langkah kekal sama, kami boleh memudahkan pengiraan dengan menjana imej bising pada cap waktu tertentu. Menggunakan teknik pengiraan semula pasangan membolehkan kami memudahkan lagi persamaan.
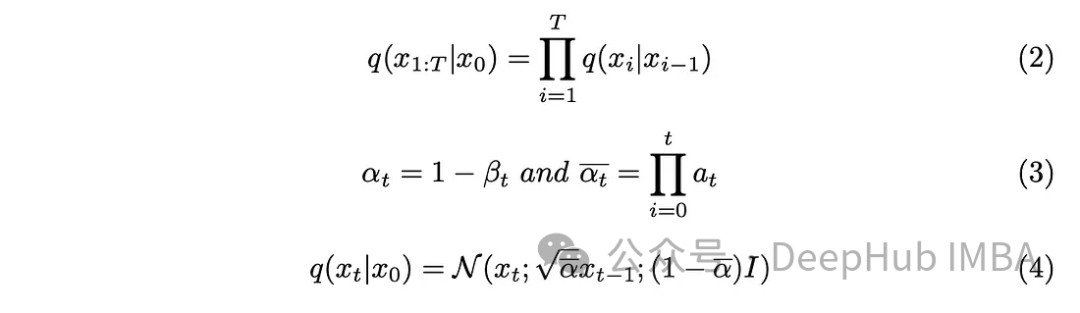
Menggabungkan parameter baharu yang diperkenalkan dalam persamaan (3) ke dalam persamaan (2), bangunkan persamaan (2), dan dapatkan hasilnya.
Kami telah memperkenalkan hingar pada imej dan langkah seterusnya ialah melakukan operasi songsang. Melainkan kita mengetahui keadaan awal, iaitu imej yang tidak dinafikan pada t = 0, adalah mustahil untuk melaksanakan proses terbalik secara matematik untuk menafikan imej tersebut. Matlamat kami adalah untuk mencuba secara langsung daripada hingar untuk mencipta imej baharu, dan di sini terdapat kekurangan maklumat tentang hasilnya. Oleh itu, saya perlu mencipta cara untuk mengecilkan imej secara progresif tanpa mengetahui hasilnya. Jadi penyelesaiannya muncul untuk menggunakan model pembelajaran mendalam untuk menganggarkan fungsi matematik yang kompleks ini.
Dengan sedikit latar belakang matematik, model akan menghampiri persamaan (5). Satu perincian yang perlu diberi perhatian ialah kami akan berpegang pada kertas DDPM asal dan memastikan varians tetap, walaupun model itu juga boleh mempelajarinya.
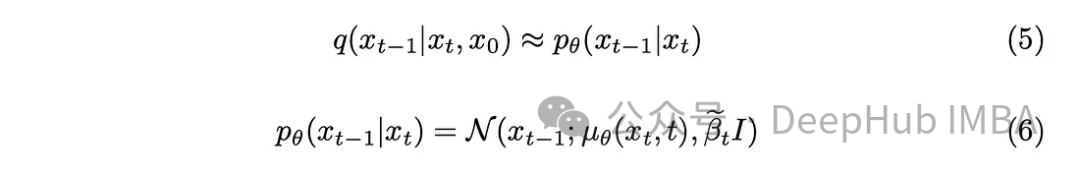
Tugas model adalah untuk meramalkan purata bunyi yang ditambah antara cap masa semasa dan cap masa sebelumnya. Ini boleh menghilangkan bunyi bising dengan berkesan dan mencapai kesan yang diingini. Tetapi bagaimana jika matlamat kita adalah untuk meminta model meramalkan bunyi yang ditambahkan daripada "imej asal" ke cap waktu terakhir
Melainkan kita tahu imej awal tanpa bunyi, ia adalah mencabar secara matematik untuk melakukan proses terbalik, Mari mulakan? dengan mentakrifkan varians posterior.

Tugas model adalah untuk meramalkan bunyi yang ditambahkan pada imej pada cap masa t daripada imej awal. Proses ke hadapan membolehkan kami melakukan operasi ini, bermula dengan imej yang jelas dan berkembang kepada imej yang bising pada cap waktu t.
Kami mengandaikan bahawa seni bina model yang digunakan untuk membuat ramalan akan menjadi U-Net. Matlamat fasa latihan ialah: untuk setiap imej dalam set data, pilih cap masa secara rawak dalam julat [0, T] dan hitung proses resapan ke hadapan. Ini menghasilkan imej yang jelas, agak bising, serta bunyi sebenar yang digunakan. Model ini kemudiannya digunakan untuk meramalkan bunyi yang ditambahkan pada imej menggunakan pemahaman kita tentang proses songsang. Dengan hingar sebenar dan ramalan, kami nampaknya telah mengalami masalah pembelajaran mesin yang diselia.
Persoalan utama datang, fungsi kerugian manakah yang patut kita gunakan untuk melatih model kita Memandangkan kita berhadapan dengan ruang terpendam kemungkinan, perbezaan Kullback-Leibler (KL) adalah pilihan yang sesuai.
Kl divergence mengukur perbezaan antara dua taburan kebarangkalian, dalam kes kami, taburan yang diramalkan oleh model dan taburan yang dijangkakan. Menggabungkan perbezaan KL ke dalam fungsi kehilangan bukan sahaja membimbing model untuk menghasilkan ramalan yang tepat, tetapi juga memastikan perwakilan ruang terpendam mematuhi struktur kebarangkalian yang dikehendaki.
Pebezaan KL boleh dianggarkan sebagai fungsi kehilangan L2, jadi fungsi kehilangan berikut boleh diperolehi:
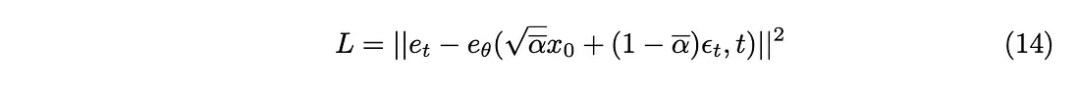
Akhirnya kami mendapat algoritma latihan yang dicadangkan dalam kertas.

Proses terbalik telah dijelaskan, berikut adalah cara menggunakannya. Bermula dari imej rawak sepenuhnya pada masa T, dan menggunakan proses terbalik T kali, akhirnya kita mencapai masa 0. Ini membentuk algoritma kedua yang digariskan dalam artikel ini

Kami mempunyai banyak parameter yang berbeza beta, beta_tildes, alpha, alpha_hat dan sebagainya. Saya masih tidak tahu bagaimana untuk memilih parameter ini. Tetapi satu-satunya parameter yang diketahui pada ketika ini ialah T, yang ditetapkan kepada 1000.
Untuk semua parameter yang disenaraikan, pemilihannya bergantung pada beta. Dari satu segi, Beta menentukan jumlah hingar yang ingin kami tambahkan pada setiap langkah. Oleh itu, untuk memastikan kejayaan algoritma, pemilihan beta yang teliti adalah penting. Oleh kerana terdapat terlalu banyak parameter lain, sila rujuk kertas tersebut.
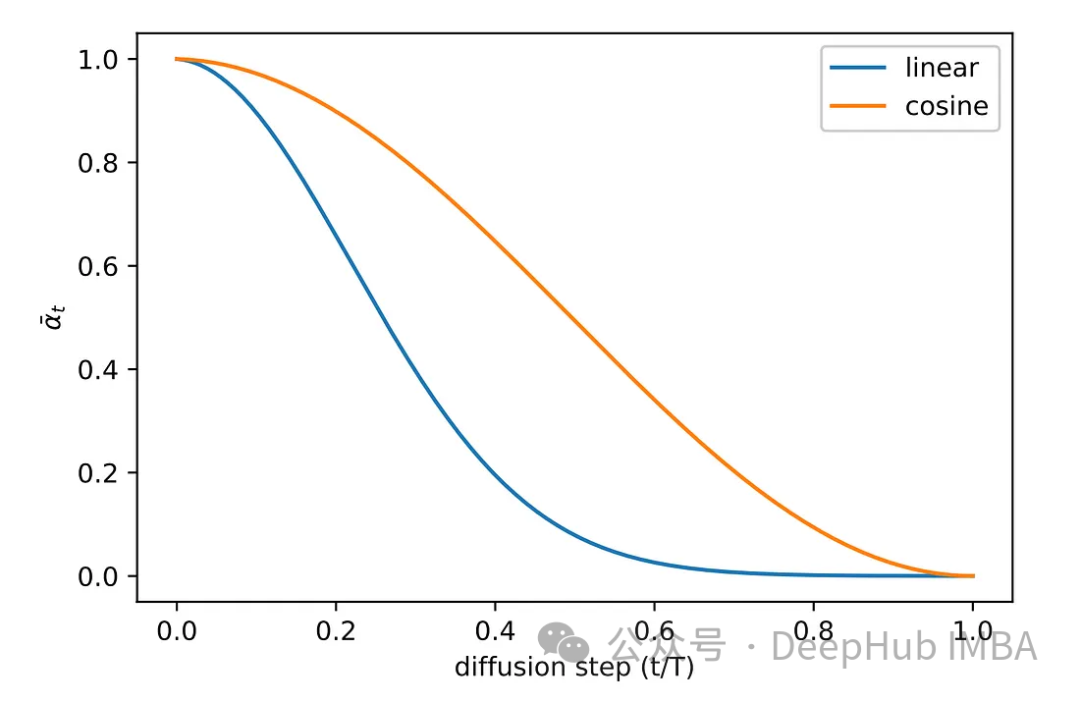
Pelbagai kaedah persampelan telah diterokai semasa fasa eksperimen kertas asal. Imej kaedah pensampelan linear asal sama ada menerima bunyi yang tidak mencukupi atau menjadi terlalu bising. Untuk menyelesaikan masalah ini, kaedah lain yang lebih biasa digunakan, iaitu pensampelan kosinus. Pensampelan kosinus memberikan penambahan bunyi yang lebih lancar dan konsisten.
Kami akan menggunakan seni bina U-Net untuk ramalan hingar Sebab U-Net dipilih kerana U-Net adalah yang terbaik untuk pemprosesan imej, menangkap spatial dan ciri. peta, dan menyediakan dan memasukkan seni bina Ideal untuk saiz output yang sama.
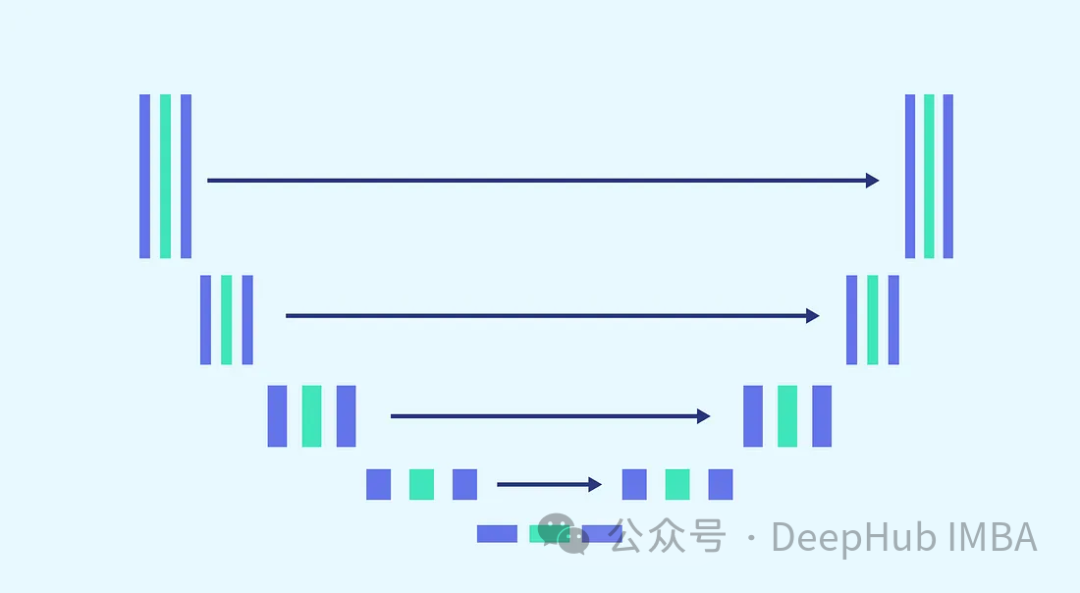
Memandangkan kerumitan tugas dan keperluan untuk menggunakan model yang sama untuk setiap langkah (di mana model perlu dapat menapis imej yang bising sepenuhnya dan imej yang sedikit bising dengan berat yang sama), menala model adalah suatu kemestian yang amat diperlukan. Ini termasuk menggabungkan blok yang lebih kompleks dan memperkenalkan kesedaran tentang cap masa yang digunakan melalui langkah pembenaman sinusoidal. Tujuan penambahbaikan ini adalah untuk menjadikan model itu pakar dalam menafikan tugas. Kami akan memperkenalkan setiap blok sebelum meneruskan untuk membina model lengkap.
Untuk memenuhi keperluan untuk meningkatkan kerumitan model, blok lilitan memainkan peranan yang penting. Kita tidak boleh hanya bergantung pada blok asas dalam kertas u-net di sini, kita akan menggabungkannya dengan ConvNext.
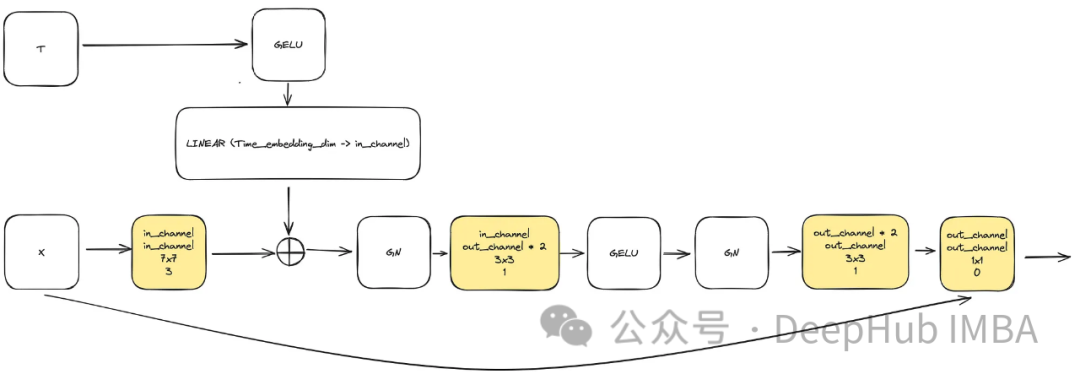
Input terdiri daripada "x" yang mewakili imej dan visualisasi cap waktu terbenam "t" bersaiz "time_embedding_dim". Sepanjang proses, blok memainkan peranan penting dalam mempelajari peta spatial dan ciri kerana kerumitannya dan sambungan baki kepada input dan lapisan akhir.
class ConvNextBlock(nn.Module):def __init__(self,in_channels,out_channels,mult=2,time_embedding_dim=None,norm=True,group=8,):super().__init__()self.mlp = (nn.Sequential(nn.GELU(), nn.Linear(time_embedding_dim, in_channels))if time_embedding_dimelse None) self.in_conv = nn.Conv2d(in_channels, in_channels, 7, padding=3, groups=in_channels) self.block = nn.Sequential(nn.GroupNorm(1, in_channels) if norm else nn.Identity(),nn.Conv2d(in_channels, out_channels * mult, 3, padding=1),nn.GELU(),nn.GroupNorm(1, out_channels * mult),nn.Conv2d(out_channels * mult, out_channels, 3, padding=1),) self.residual_conv = (nn.Conv2d(in_channels, out_channels, 1)if in_channels != out_channelselse nn.Identity()) def forward(self, x, time_embedding=None):h = self.in_conv(x)if self.mlp is not None and time_embedding is not None:assert self.mlp is not None, "MLP is None"h = h + rearrange(self.mlp(time_embedding), "b c -> b c 1 1")h = self.block(h)return h + self.residual_conv(x)
Salah satu blok utama dalam model ialah blok pemasukan cap masa sinusoidal, yang membolehkan pengekodan cap masa yang diberikan untuk mengekalkan maklumat tentang masa semasa yang diperlukan untuk model menyahkod, kerana Model akan digunakan untuk semua cap masa yang berbeza.
Ini adalah pelaksanaan yang sangat klasik, dan ia digunakan di pelbagai tempat, kami akan menampal kod secara terus
class SinusoidalPosEmb(nn.Module):def __init__(self, dim, theta=10000):super().__init__()self.dim = dimself.theta = theta def forward(self, x):device = x.devicehalf_dim = self.dim // 2emb = math.log(self.theta) / (half_dim - 1)emb = torch.exp(torch.arange(half_dim, device=device) * -emb)emb = x[:, None] * emb[None, :]emb = torch.cat((emb.sin(), emb.cos()), dim=-1)return emb
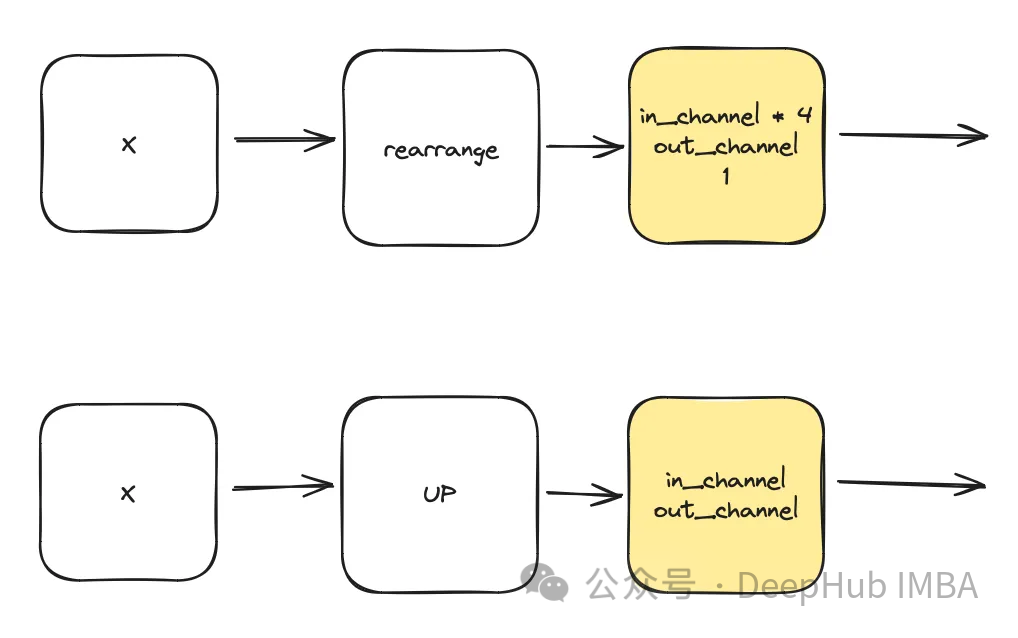
class DownSample(nn.Module):def __init__(self, dim, dim_out=None):super().__init__()self.net = nn.Sequential(Rearrange("b c (h p1) (w p2) -> b (c p1 p2) h w", p1=2, p2=2),nn.Conv2d(dim * 4, default(dim_out, dim), 1),) def forward(self, x):return self.net(x) class Upsample(nn.Module):def __init__(self, dim, dim_out=None):super().__init__()self.net = nn.Sequential(nn.Upsample(scale_factor=2, mode="nearest"),nn.Conv2d(dim, dim_out or dim, kernel_size=3, padding=1),) def forward(self, x):return self.net(x)al-layerTemporee
Modul ini menggunakan ini untuk mencipta perwakilan masa berdasarkan cap masa yang diberikan t. Output perceptron berbilang lapisan (MLP) ini juga akan berfungsi sebagai input "t" kepada semua blok ConvNext yang diubah suai.
Di sini, "malap" ialah hiperparameter model, menunjukkan bilangan saluran yang diperlukan untuk blok pertama. Ia berfungsi sebagai pengiraan asas untuk bilangan saluran dalam blok berikutnya.
sinu_pos_emb = SinusoidalPosEmb(dim, theta=10000) time_dim = dim * 4 time_mlp = nn.Sequential(sinu_pos_emb,nn.Linear(dim, time_dim),nn.GELU(),nn.Linear(time_dim, time_dim),)
Ini adalah komponen pilihan yang digunakan dalam unet. Perhatian membantu meningkatkan peranan sambungan sisa dalam pembelajaran. Ia memberi lebih perhatian kepada maklumat spatial penting yang diperoleh dari sebelah kiri Unet melalui mekanisme perhatian yang dikira oleh sambungan baki dan peta ciri yang dikira oleh ruang terpendam sederhana dan rendah. Ia datang daripada kertas ACC-UNet.
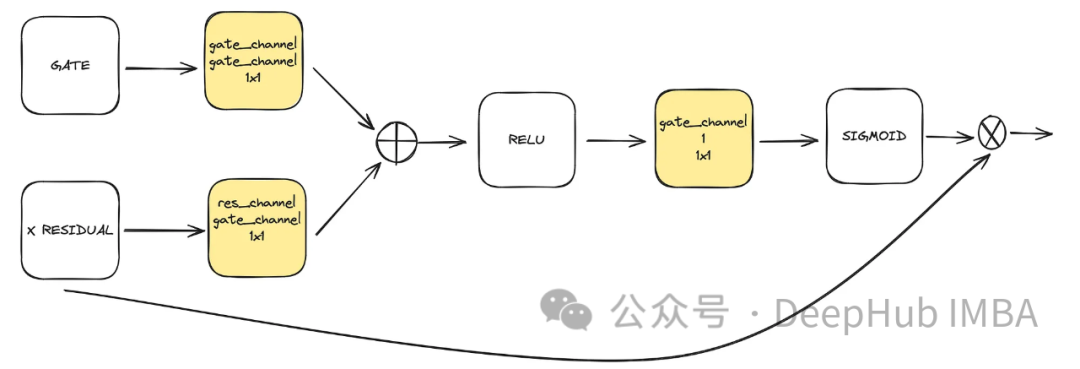
get mewakili output sampel atas blok bawah, manakala baki-x mewakili sambungan baki pada tahap di mana perhatian digunakan. 🎜🎜
class BlockAttention(nn.Module):def __init__(self, gate_in_channel, residual_in_channel, scale_factor):super().__init__()self.gate_conv = nn.Conv2d(gate_in_channel, gate_in_channel, kernel_size=1, stride=1)self.residual_conv = nn.Conv2d(residual_in_channel, gate_in_channel, kernel_size=1, stride=1)self.in_conv = nn.Conv2d(gate_in_channel, 1, kernel_size=1, stride=1)self.relu = nn.ReLU()self.sigmoid = nn.Sigmoid() def forward(self, x: torch.Tensor, g: torch.Tensor) -> torch.Tensor:in_attention = self.relu(self.gate_conv(g) + self.residual_conv(x))in_attention = self.in_conv(in_attention)in_attention = self.sigmoid(in_attention)return in_attention * x
将前面讨论的所有块(不包括注意力块)整合到一个Unet中。每个块都包含两个残差连接,而不是一个。这个修改是为了解决潜在的过度拟合问题。
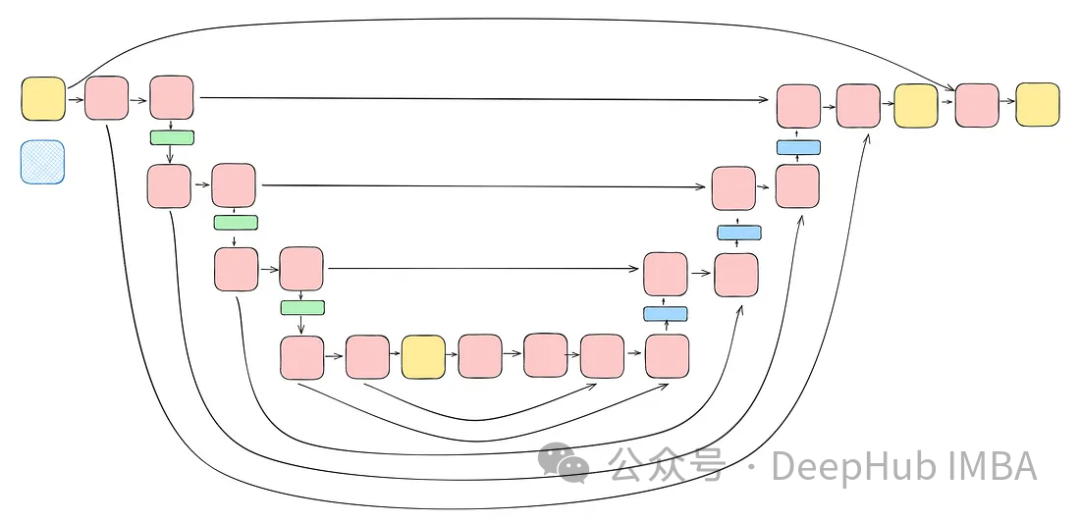
class TwoResUNet(nn.Module):def __init__(self,dim,init_dim=None,out_dim=None,dim_mults=(1, 2, 4, 8),channels=3,sinusoidal_pos_emb_theta=10000,convnext_block_groups=8,):super().__init__()self.channels = channelsinput_channels = channelsself.init_dim = default(init_dim, dim)self.init_conv = nn.Conv2d(input_channels, self.init_dim, 7, padding=3) dims = [self.init_dim, *map(lambda m: dim * m, dim_mults)]in_out = list(zip(dims[:-1], dims[1:])) sinu_pos_emb = SinusoidalPosEmb(dim, theta=sinusoidal_pos_emb_theta) time_dim = dim * 4 self.time_mlp = nn.Sequential(sinu_pos_emb,nn.Linear(dim, time_dim),nn.GELU(),nn.Linear(time_dim, time_dim),) self.downs = nn.ModuleList([])self.ups = nn.ModuleList([])num_resolutions = len(in_out) for ind, (dim_in, dim_out) in enumerate(in_out):is_last = ind >= (num_resolutions - 1) self.downs.append(nn.ModuleList([ConvNextBlock(in_channels=dim_in,out_channels=dim_in,time_embedding_dim=time_dim,group=convnext_block_groups,),ConvNextBlock(in_channels=dim_in,out_channels=dim_in,time_embedding_dim=time_dim,group=convnext_block_groups,),DownSample(dim_in, dim_out)if not is_lastelse nn.Conv2d(dim_in, dim_out, 3, padding=1),])) mid_dim = dims[-1]self.mid_block1 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim)self.mid_block2 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim) for ind, (dim_in, dim_out) in enumerate(reversed(in_out)):is_last = ind == (len(in_out) - 1)is_first = ind == 0 self.ups.append(nn.ModuleList([ConvNextBlock(in_channels=dim_out + dim_in,out_channels=dim_out,time_embedding_dim=time_dim,group=convnext_block_groups,),ConvNextBlock(in_channels=dim_out + dim_in,out_channels=dim_out,time_embedding_dim=time_dim,group=convnext_block_groups,),Upsample(dim_out, dim_in)if not is_lastelse nn.Conv2d(dim_out, dim_in, 3, padding=1)])) default_out_dim = channelsself.out_dim = default(out_dim, default_out_dim) self.final_res_block = ConvNextBlock(dim * 2, dim, time_embedding_dim=time_dim)self.final_conv = nn.Conv2d(dim, self.out_dim, 1) def forward(self, x, time):b, _, h, w = x.shapex = self.init_conv(x)r = x.clone() t = self.time_mlp(time) unet_stack = []for down1, down2, downsample in self.downs:x = down1(x, t)unet_stack.append(x)x = down2(x, t)unet_stack.append(x)x = downsample(x) x = self.mid_block1(x, t)x = self.mid_block2(x, t) for up1, up2, upsample in self.ups:x = torch.cat((x, unet_stack.pop()), dim=1)x = up1(x, t)x = torch.cat((x, unet_stack.pop()), dim=1)x = up2(x, t)x = upsample(x) x = torch.cat((x, r), dim=1)x = self.final_res_block(x, t) return self.final_conv(x)
最后我们介绍一下扩散是如何实现的。由于我们已经介绍了用于正向、逆向和采样过程的所有数学理论,所里这里将重点介绍代码。
class DiffusionModel(nn.Module):SCHEDULER_MAPPING = {"linear": linear_beta_schedule,"cosine": cosine_beta_schedule,"sigmoid": sigmoid_beta_schedule,} def __init__(self,model: nn.Module,image_size: int,*,beta_scheduler: str = "linear",timesteps: int = 1000,schedule_fn_kwargs: dict | None = None,auto_normalize: bool = True,) -> None:super().__init__()self.model = model self.channels = self.model.channelsself.image_size = image_size self.beta_scheduler_fn = self.SCHEDULER_MAPPING.get(beta_scheduler)if self.beta_scheduler_fn is None:raise ValueError(f"unknown beta schedule {beta_scheduler}") if schedule_fn_kwargs is None:schedule_fn_kwargs = {} betas = self.beta_scheduler_fn(timesteps, **schedule_fn_kwargs)alphas = 1.0 - betasalphas_cumprod = torch.cumprod(alphas, dim=0)alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)posterior_variance = (betas * (1.0 - alphas_cumprod_prev) / (1.0 - alphas_cumprod)) register_buffer = lambda name, val: self.register_buffer(name, val.to(torch.float32)) register_buffer("betas", betas)register_buffer("alphas_cumprod", alphas_cumprod)register_buffer("alphas_cumprod_prev", alphas_cumprod_prev)register_buffer("sqrt_recip_alphas", torch.sqrt(1.0 / alphas))register_buffer("sqrt_alphas_cumprod", torch.sqrt(alphas_cumprod))register_buffer("sqrt_one_minus_alphas_cumprod", torch.sqrt(1.0 - alphas_cumprod))register_buffer("posterior_variance", posterior_variance) timesteps, *_ = betas.shapeself.num_timesteps = int(timesteps) self.sampling_timesteps = timesteps self.normalize = normalize_to_neg_one_to_one if auto_normalize else identityself.unnormalize = unnormalize_to_zero_to_one if auto_normalize else identity @torch.inference_mode()def p_sample(self, x: torch.Tensor, timestamp: int) -> torch.Tensor:b, *_, device = *x.shape, x.devicebatched_timestamps = torch.full((b,), timestamp, device=device, dtype=torch.long) preds = self.model(x, batched_timestamps) betas_t = extract(self.betas, batched_timestamps, x.shape)sqrt_recip_alphas_t = extract(self.sqrt_recip_alphas, batched_timestamps, x.shape)sqrt_one_minus_alphas_cumprod_t = extract(self.sqrt_one_minus_alphas_cumprod, batched_timestamps, x.shape) predicted_mean = sqrt_recip_alphas_t * (x - betas_t * preds / sqrt_one_minus_alphas_cumprod_t) if timestamp == 0:return predicted_meanelse:posterior_variance = extract(self.posterior_variance, batched_timestamps, x.shape)noise = torch.randn_like(x)return predicted_mean + torch.sqrt(posterior_variance) * noise @torch.inference_mode()def p_sample_loop(self, shape: tuple, return_all_timesteps: bool = False) -> torch.Tensor:batch, device = shape[0], "mps" img = torch.randn(shape, device=device)# This cause me a RunTimeError on MPS device due to MPS back out of memory# No ideas how to resolve it at this point # imgs = [img] for t in tqdm(reversed(range(0, self.num_timesteps)), total=self.num_timesteps):img = self.p_sample(img, t)# imgs.append(img) ret = img # if not return_all_timesteps else torch.stack(imgs, dim=1) ret = self.unnormalize(ret)return ret def sample(self, batch_size: int = 16, return_all_timesteps: bool = False) -> torch.Tensor:shape = (batch_size, self.channels, self.image_size, self.image_size)return self.p_sample_loop(shape, return_all_timesteps=return_all_timesteps) def q_sample(self, x_start: torch.Tensor, t: int, noise: torch.Tensor = None) -> torch.Tensor:if noise is None:noise = torch.randn_like(x_start) sqrt_alphas_cumprod_t = extract(self.sqrt_alphas_cumprod, t, x_start.shape)sqrt_one_minus_alphas_cumprod_t = extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise def p_loss(self,x_start: torch.Tensor,t: int,noise: torch.Tensor = None,loss_type: str = "l2",) -> torch.Tensor:if noise is None:noise = torch.randn_like(x_start)x_noised = self.q_sample(x_start, t, noise=noise)predicted_noise = self.model(x_noised, t) if loss_type == "l2":loss = F.mse_loss(noise, predicted_noise)elif loss_type == "l1":loss = F.l1_loss(noise, predicted_noise)else:raise ValueError(f"unknown loss type {loss_type}")return loss def forward(self, x: torch.Tensor) -> torch.Tensor:b, c, h, w, device, img_size = *x.shape, x.device, self.image_sizeassert h == w == img_size, f"image size must be {img_size}" timestamp = torch.randint(0, self.num_timesteps, (1,)).long().to(device)x = self.normalize(x)return self.p_loss(x, timestamp)扩散过程是训练部分的模型。它打开了一个采样接口,允许我们使用已经训练好的模型生成样本。
对于训练部分,我们设置了37,000步的训练,每步16个批次。由于GPU内存分配限制,图像大小被限制为128x128。使用指数移动平均(EMA)模型权重每1000步生成样本以平滑采样,并保存模型版本。
在最初的1000步训练中,模型开始捕捉一些特征,但仍然错过了某些区域。在10000步左右,这个模型开始产生有希望的结果,进步变得更加明显。在3万步的最后,结果的质量显著提高,但仍然存在黑色图像。这只是因为模型没有足够的样本种类,真实图像的数据分布并没有完全映射到高斯分布。

有了最终的模型权重,我们可以生成一些图片。尽管由于128x128的尺寸限制,图像质量受到限制,但该模型的表现还是不错的。

注:本文使用的数据集是森林地形的卫星图片,具体获取方式请参考源代码中的ETL部分。
我们已经完整的介绍了有关扩散模型的必要知识,并且使用Pytorch进行了完整的实现,本文的代码:
https://github.com/Camaltra/this-is-not-real-aerial-imagery/
Atas ialah kandungan terperinci Melaksanakan model resapan penyingkiran hingar menggunakan PyTorch. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




