
Selepas "disokong" oleh GPT-4, Copilot juga digilai oleh Terence Tao.
Dia secara terang-terangan mengatakan bahawa apabila memprogramkan, Copilot boleh meramalkan secara langsung apa yang akan dia lakukan seterusnya.
Dengan Copilot, penyelidikan menjadi lebih mudah, Tao Zhexuan juga menggunakannya untuk membantunya menyelesaikan hasil penyelidikannya yang terkini.

Tao Zhexuan berkata bahawa bahagian kertas ini sebenarnya hanya mempunyai satu halaman.
Tetapi untuk melengkapkan bukti satu halaman ini, dia menulis lebih daripada 200 baris kod, menggunakan bahasa pengaturcaraan Lean4 yang baru dipelajari.

Halaman GitHub kod awam Tao Zhexuan menunjukkan bahawa Copilot telah meningkatkan kelajuan menulis kod lebih separuh.
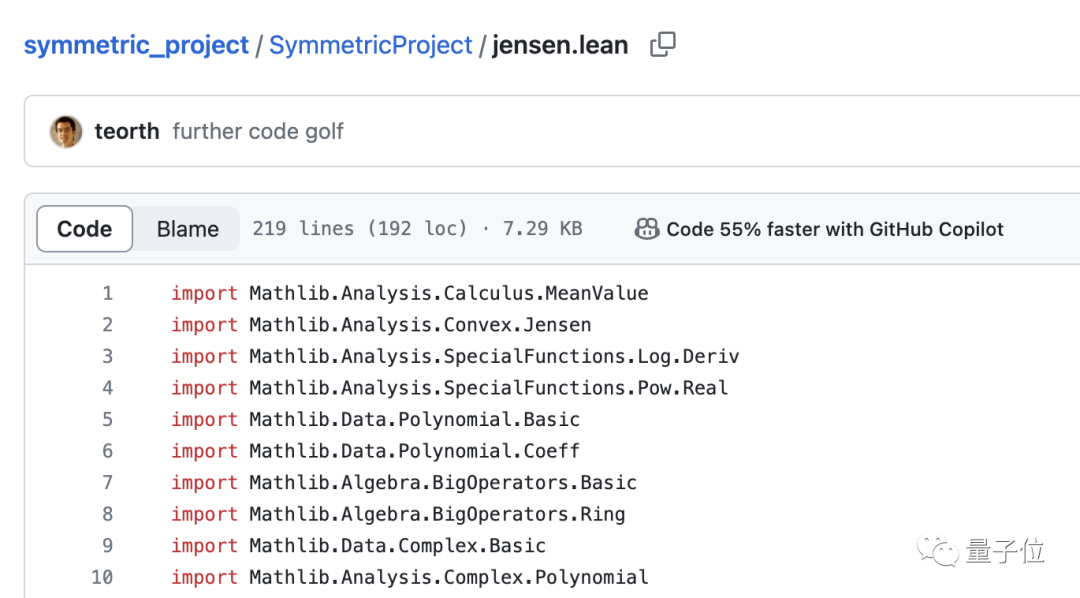
Tao Zhexuan berkata bahawa sebab mengapa dia memilih Lean4 adalah kerana "strategi penulisan semula"nya, iaitu untuk melaksanakan penggantian separa yang disasarkan bagi ungkapan panjang.
Sebagai contoh, jika fungsi kompleks f(x) ditakrifkan, apabila kita ingin memasukkan ungkapan f(114514), kita boleh terus "menulis semula" x ke 114514 menggunakan kod.
Tao Zhexuan berkata bahawa ciri ini tidak begitu mudah berbanding dengan LaTeX yang memerlukan input berulang formula.
Jadi, apakah hasil baharu yang diberikan oleh "bukti satu halaman" Tao Zhexuan kali ini?
Kertas kerja ini membincangkan isu berkaitan ketidaksamaan MacLaughlin.
Ketaksamaan McLaughlin ialah ketaksamaan klasik dalam matematik Ia diperoleh berdasarkan undang-undang bahawa "min aritmetik nombor nyata bukan negatif adalah lebih besar daripada atau sama dengan min geometrik".
1...yn ialah nombor nyata bukan negatif Untuk k=1...n, min Sk ditakrifkan sebagai (penyebut ialah bilangan sebutan dalam pengangka):
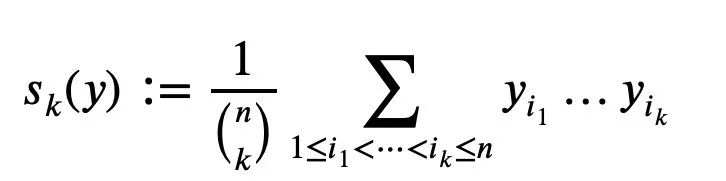 Ia kelihatan sebagai pekali ternormal bagi polinomial darjah ke-n dengan akar. .
Ia kelihatan sebagai pekali ternormal bagi polinomial darjah ke-n dengan akar. .
Dalam kalkulus, terdapat juga ketaksamaan Newton klasik:
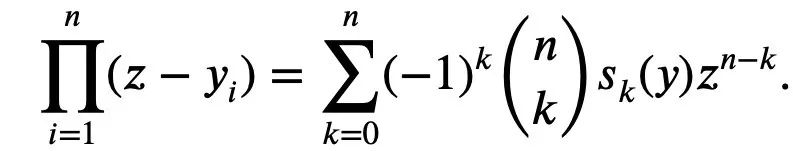
Untuk mana-mana 1≤k semuanya bukan negatif, ketaksamaan Newton hanya boleh menggambarkan ketaksamaan Mike. Ketaksamaan Laurin: Tetapi jika sekatan ini tidak ditambah, iaitu kewujudan istilah negatif dibenarkan, ketaksamaan Maclaurin tidak boleh dinyatakan dengan ketaksamaan Newton. Jadi untuk situasi di mana istilah negatif mungkin wujud dalam ketaksamaan Newton, Tao Zhexuan mencadangkan satu set varian ketaksamaan baharu: Untuk sebarang r>0 dan 1≤ℓ≤n, Persamaan 2 atau Persamaan 3 mestilah benar. . formula 1 sebelumnya dan ketaksamaan segitiga boleh diperolehi: Jadi kita hanya perlu mewujudkan sempadan bawah: Ambil nilai mutlak P(z) dan kemudian ambil logaritma untuk mendapatkan: Oleh kerana bagi sebarang nombor nyata t, t ↦ log(e t+a) ialah Convexity dan a>0, anda boleh mendapatkan ketaksamaan: Apabila a=r2, t=2log yj, anda boleh mendapat: n|=1 yang dinormalkan, formula berikut memegang: Alamat kertas: https://arxiv.org/abs/2310.05328 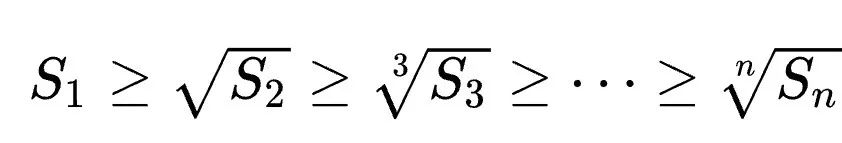
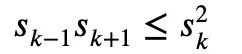
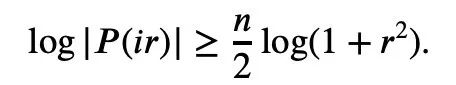
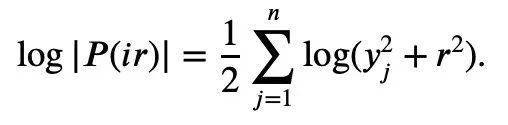
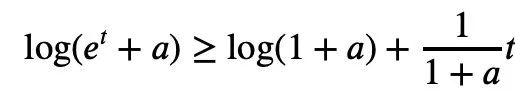
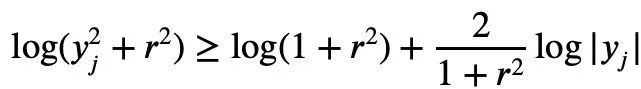
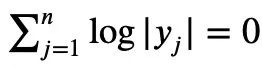
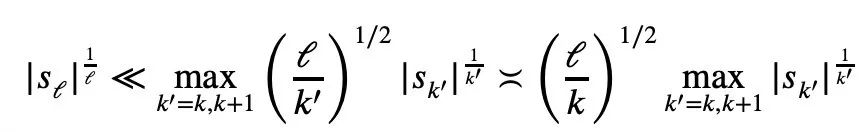


Atas ialah kandungan terperinci Crazy Amway Tao Zhexuan: Ia membantu saya melengkapkan bukti satu halaman dan juga meneka proses saya yang seterusnya. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Bagaimana untuk memulihkan video yang telah dialih keluar secara rasmi daripada Douyin
Bagaimana untuk memulihkan video yang telah dialih keluar secara rasmi daripada Douyin
 js untuk menjana nombor rawak
js untuk menjana nombor rawak
 Berapa tinggi Ethereum akan pergi?
Berapa tinggi Ethereum akan pergi?
 Bagaimana untuk memulihkan fail yang dipadam pada komputer
Bagaimana untuk memulihkan fail yang dipadam pada komputer
 Berapa tahun anda perlu membayar insurans perubatan untuk menikmati insurans perubatan sepanjang hayat?
Berapa tahun anda perlu membayar insurans perubatan untuk menikmati insurans perubatan sepanjang hayat?
 Apa yang perlu dilakukan jika tiada kursor apabila mengklik pada kotak input
Apa yang perlu dilakukan jika tiada kursor apabila mengklik pada kotak input
 Apakah yang perlu saya lakukan jika huruf Inggeris muncul apabila komputer dihidupkan dan komputer tidak boleh dihidupkan?
Apakah yang perlu saya lakukan jika huruf Inggeris muncul apabila komputer dihidupkan dan komputer tidak boleh dihidupkan?
 Bagaimana untuk membuat wifi maya dalam win7
Bagaimana untuk membuat wifi maya dalam win7