Cari laluan terpendek antara mana-mana dua nod menggunakan algoritma Floyd-Warshal

C++ mempunyai makro, yang ditakrifkan sebagai sekeping kod atau nilai yang dijangkakan, dan ia akan digunakan semula pada bila-bila masa pengguna memerlukannya. Algoritma Floyd-Walshall ialah proses mencari laluan terpendek antara semua pasangan bucu dalam graf berwajaran tertentu. Algoritma mengikut pendekatan pengaturcaraan dinamik untuk mencari graf berat minimum.

Mari kita fahami maksud Algoritma Freud-Walshire melalui gambar rajah -

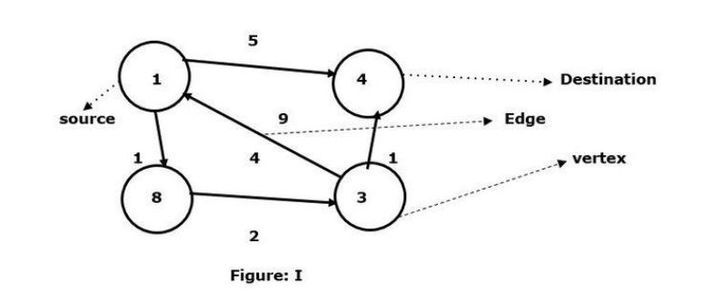
Dengan bucu 1 sebagai sumber dan bucu 4 sebagai destinasi, cari jalan terpendek di antara mereka.

Kami telah melihat bahawa terdapat dua laluan yang boleh disambungkan ke puncak sasaran 4.

• 1 -> 4 – Tepi mempunyai berat 5

• 1 -> 8 -> 3 ->

Dalam graf I yang diberikan, kita melihat tepi minimum yang menghubungkan dua bucu. Jadi di sini laluan dari bucu 8 ke bucu 3 menghubungkan bucu 1 ke bucu 4 dan tepi ialah 4. Sebaliknya, terdapat tepi terarah dari bucu 1 ke bucu 4, dan berat tepi ialah 5.

Sekarang kita bandingkan dua pemberat iaitu 4 dan 5. Oleh itu, di sini 4 ialah berat minimum graf yang dikira mengikut algoritma Floyd Warshall.

Dalam artikel ini, kami akan menggunakan algoritma Floyd Warshall untuk mencari laluan terpendek antara mana-mana dua nod yang diberikan.

Tatabahasa

Sintaks berikut digunakan dalam program -

data_type[][] array_name;

Parameter

data_type[][] - Jenis data yang disebut oleh pengguna. Tatasusunan pertama mewakili baris dan tatasusunan kedua mewakili lajur. Jadi, ini mewakili tatasusunan dua dimensi.

array_name - Nama yang diberikan kepada array.

Algoritma

• Kami akan memulakan program dengan fail pengepala 'iostream' dan mentakrifkan lokasi makro sebagai 'INF' (infiniti) kerana kemudiannya ia akan memenuhi matriks tatasusunan 2D dan pernyataan if-else.

• Seterusnya, kami mencipta definisi fungsi global yang dipanggil 'printPath' dan menerima tiga parameter, 'parent[]', 'i' dan 'j' untuk mengesahkan bahawa laluan itu wujud.

• Kemudian kita mulakan fungsi utama dan simpan nilai ‘4’ ke dalam pembolehubah ‘V’, yang mewakili bilangan bucu. Kedua, simpan nilai dalam bentuk matriks bersebelahan ke dalam pembolehubah ‘dist[V][V]’. Seperti yang kita ketahui, dist[i][j] mewakili matriks 2D, yang mentakrifkan berat tepi daripada ‘i’ hingga ‘j’, dengan menyimpan matriks bersebelahan.

• Seterusnya, kami memulakan tatasusunan 2D untuk pembolehubah ‘induk’, dengan saiz [V][V].

Dalam pembolehubah ini kita gunakan untuk memaparkan setiap pasangan bucu 'i' dan 'j' w.r.t 'ibu bapa[i][j]'< /b>.

• Dengan menggunakan dua gelung bersarang kita akan mencari laluan terpendek. Gelung untuk pertama berulang ke atas baris dalam matriks. Kemudian, ulangi lajur dalam matriks melalui gelung kedua untuk dan kemudian kami akan menyemak keadaan berikut menggunakan pernyataan if-else -

• Jika (dist[i][j] != INF && i != j) { Terjemahan bahasa Cina bagi ibu bapa[i][j] = i;}

  ialah: ibu bapa[i][j] = i;}

  Dalam pernyataan if, kami menggunakan operator 'and' (&&) untuk menyatakan dua syarat jika kedua-dua syarat dipenuhi, maka 'i' akan disimpan ke dalam 'parent[i][j]' , dengan itu mengesahkan bahawa. jalan itu wujud.

• Lain-lain{ Terjemahan bahasa Cina bagi parent[i][j] = -1;}

  ialah: parent[i][j] = -1;}

  Dalam pernyataan else, kami memulakan "-1" kepada "ibu bapa[i][j]" untuk mengesahkan bahawa laluan itu tidak wujud.

• Kini kita mulakan dengan tiga gelung untuk bersarang dan menggunakan bucu k dalam julat dari 0 hingga V-1, dengan bantuan julat ini jarak dan laluan terpendek kita akan dikemas kini. Dalam gelung bersarang ketiga kami menggunakan keadaan berikut seperti

if (dist[i][j] < dist[i][k] + dist[k][j]){
   dist[i][j] = dist[i][k] + dist[k][j]; 
   parent[i][j] = parent[k][j];	
}

#include <iostream> 
using namespace std; 
#define INF 1000000000 // Infinity

void printPath(int parent[], int i, int j) {
   if (i == j) 
      cout << i << " "; 
   else if (parent[j] == -1) 
     cout << "No path exists"; 
   else
   { 
      printPath(parent, i, parent[j]); 
      cout << j << " "; 
   }
} 

int main() 
{
   int V = 4; 
   // V represent number of vertices
   int dist[V][V] = {{0, 2, INF, 4}, 
      {6, 0, 5, 3}, 
      {INF, 10, 0, 1}, 
      {7, 9, 8, 0}}; 
   // Represent the graph using adjacency matrix

   // Apply the Floyd Warshall algorithm to find the shortest paths
   int parent[V][V];
   for (int i = 0; i < V; i++) 
   { 
      for (int j = 0; j < V; j++) 
      {
         if (dist[i][j] != INF && i != j)
         parent[i][j] = i;
         else
         parent[i][j] = -1;
      }
   }
   // update the path and distance using the k vertex range from 0 to V-1.
   for (int k = 0; k < V; k++) 
   { 
      for (int i = 0; i < V; i++) 
      { 
         for (int j = 0; j < V; j++) 
         { 
            if (dist[i][j] > dist[i][k] + dist[k][j]) 
            {
               dist[i][j] = dist[i][k] + dist[k][j];
               parent[i][j] = parent[k][j];	
            }
         }
      }
   }

   // Print shortest distances and paths between all pairs of vertices
   for (int i = 0; i < V; i++) 
   { 
      for (int j = 0; j < V; j++) 
      { 
         cout << "The Shortest distance between " << i << " and " << j << " is ";
         if (dist[i][j] == INF) 
            cout << "INF "; 
         else
            cout << dist[i][j] << " ";

         cout << "and the shortest path is:- ";
         printPath(parent[i], i, j);
         cout << endl;
      } 
   } 

   return 0; 
}

The Shortest distance between 0 and 0 is 0 and the shortest path is:- 0 
The Shortest distance between 0 and 1 is 2 and the shortest path is:- 0 1 
The Shortest distance between 0 and 2 is 7 and the shortest path is:- 0 1 2 
The Shortest distance between 0 and 3 is 4 and the shortest path is:- 0 3 
The Shortest distance between 1 and 0 is 6 and the shortest path is:- 1 0 
The Shortest distance between 1 and 1 is 0 and the shortest path is:- 1 
The Shortest distance between 1 and 2 is 5 and the shortest path is:- 1 2 
The Shortest distance between 1 and 3 is 3 and the shortest path is:- 1 3 
The Shortest distance between 2 and 0 is 8 and the shortest path is:- 2 3 0 
The Shortest distance between 2 and 1 is 10 and the shortest path is:- 2 1 
The Shortest distance between 2 and 2 is 0 and the shortest path is:- 2 
The Shortest distance between 2 and 3 is 1 and the shortest path is:- 2 3 
The Shortest distance between 3 and 0 is 7 and the shortest path is:- 3 0 
The Shortest distance between 3 and 1 is 9 and the shortest path is:- 3 1 
The Shortest distance between 3 and 2 is 8 and the shortest path is:- 3 2 
The Shortest distance between 3 and 3 is 0 and the shortest path is:- 3