

Kluster atau analisis kelompok ialah masalah pembelajaran tanpa pengawasan. Ia sering digunakan sebagai teknik analisis data untuk menemui corak menarik dalam data, seperti segmen pelanggan berdasarkan tingkah laku mereka. Terdapat banyak algoritma pengelompokan untuk dipilih, dan tiada satu algoritma pengelompokan terbaik untuk semua situasi. Sebaliknya, adalah lebih baik untuk meneroka pelbagai algoritma pengelompokan dan konfigurasi berbeza bagi setiap algoritma. Dalam tutorial ini, anda akan mengetahui cara memasang dan menggunakan algoritma pengelompokan teratas dalam python.
Selepas melengkapkan tutorial ini, anda akan mengetahui:
Gambaran Keseluruhan Tutorial
—Daripada: "Halaman Perlombongan Data: Alat dan Teknik Pembelajaran Mesin Praktikal" 2016.
Memisahkan data biasa daripada outlier atau kelainan boleh dianggap sebagai masalah pengelompokan;
Pengkelompokan ialah teknik pembelajaran tanpa pengawasan, jadi sukar untuk menilai kualiti output mana-mana kaedah tertentu.
Di tengah-tengah semua matlamat analisis kelompok ialah konsep tahap persamaan (atau ketidakserupaan) antara objek individu yang dikelompokkan. Kaedah pengelompokan cuba mengumpulkan objek berdasarkan definisi persamaan yang diberikan kepada objek.
Setiap algoritma menyediakan pendekatan yang berbeza kepada cabaran untuk menemui kumpulan semula jadi dalam data. Tiada algoritma pengelompokan terbaik dan tiada cara mudah untuk mencari algoritma terbaik untuk data anda tanpa menggunakan eksperimen terkawal. Dalam tutorial ini, kami akan menyemak cara menggunakan setiap 10 algoritma pengelompokan popular ini daripada perpustakaan scikit-learn. Contoh-contoh ini akan memberi anda asas untuk menyalin dan menampal contoh dan menguji kaedah pada data anda sendiri. Kami tidak akan menyelidiki teori tentang cara algoritma berfungsi, dan kami tidak akan membandingkannya secara langsung. Mari kita gali sedikit lebih dalam.
Dalam bahagian ini, kami akan menyemak cara menggunakan 10 algoritma pengelompokan yang popular dalam scikit-learn. Ini termasuk contoh pemasangan model dan contoh visualisasi hasil. Contoh-contoh ini adalah untuk menampal dan menyalin ke dalam projek anda sendiri dan menggunakan kaedah pada data anda sendiri.
Mula-mula, mari pasang perpustakaan. Jangan langkau langkah ini kerana anda perlu memastikan anda memasang versi terkini. Anda boleh memasang repositori scikit-learn menggunakan pemasang Python pip seperti ini:
sudo pip install scikit-learn
Seterusnya, mari sahkan bahawa perpustakaan telah dipasang dan anda menggunakan versi moden. Jalankan skrip berikut untuk mengeluarkan nombor versi perpustakaan.
# 检查 scikit-learn 版本 import sklearn print(sklearn.__version__)
Apabila anda menjalankan contoh, anda sepatutnya melihat nombor versi berikut atau lebih tinggi.
0.22.1
Kami akan menggunakan fungsi make_classification () untuk mencipta set data klasifikasi binari ujian. Set data akan mempunyai 1000 contoh, dengan dua ciri input dan satu kelompok bagi setiap kelas. Kelompok ini boleh dilihat dalam dua dimensi, jadi kita boleh memplot data dalam plot serakan dan mewarnai titik dalam plot mengikut kelompok yang ditentukan.
Ini akan membantu untuk memahami sejauh mana kluster dikenal pasti, sekurang-kurangnya pada masalah ujian. Kelompok dalam masalah ujian ini adalah berdasarkan Gaussians multivariate, dan tidak semua algoritma pengelompokan berkesan untuk mengenal pasti jenis kelompok ini. Oleh itu, keputusan dalam tutorial ini tidak boleh digunakan sebagai asas untuk membandingkan kaedah umum. Disenaraikan di bawah ialah contoh mencipta dan meringkaskan set data kelompok sintetik.
# 综合分类数据集 from numpy import where from sklearn.datasets import make_classification from matplotlib import pyplot # 定义数据集 X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 为每个类的样本创建散点图 for class_value in range(2): # 获取此类的示例的行索引 row_ix = where(y == class_value) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
Menjalankan contoh ini akan mencipta set data berkelompok sintetik dan kemudian mencipta plot serakan data input, dengan titik diwarnai oleh label kelas (kelompok ideal). Kami dapat melihat dengan jelas dua kumpulan data yang berbeza dalam dua dimensi dan berharap algoritma pengelompokan automatik dapat mengesan kumpulan ini.
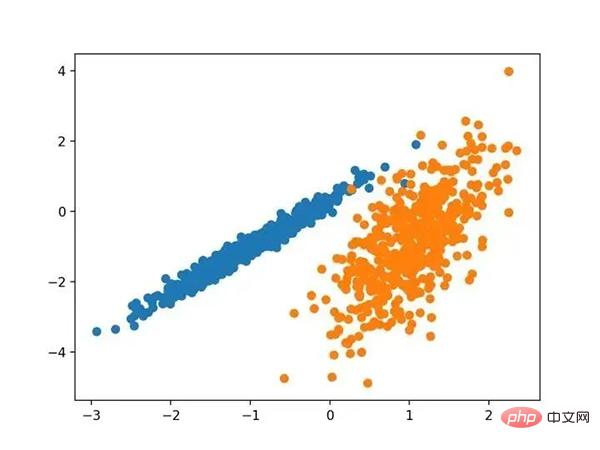
Scatterplot bagi set data pengelompokan sintetik bagi titik teduhan berkelompok yang diketahui
Seterusnya, kita boleh mula melihat hasil yang digunakan pada set data ini Contoh algoritma pengelompokan. Saya telah membuat beberapa percubaan minimum untuk menyesuaikan setiap kaedah kepada set data.
Penyebaran Perkaitan melibatkan mencari satu set contoh yang terbaik meringkaskan data.
Ia dilaksanakan melalui kelas AffinityPropagation, konfigurasi utama untuk diselaraskan adalah untuk menetapkan "Dampening" daripada 0.5 kepada 1, mungkin juga "Preferences".
Contoh penuh disenaraikan di bawah.
# 亲和力传播聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import AffinityPropagation from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = AffinityPropagation(damping=0.9) # 匹配模型 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
Jalankan contoh agar sesuai dengan model pada set data latihan dan ramalkan kelompok untuk setiap contoh dalam set data. Plot berselerak kemudian dibuat, diwarnai oleh kelompok yang ditetapkan. Dalam kes ini saya tidak dapat mencapai keputusan yang baik.
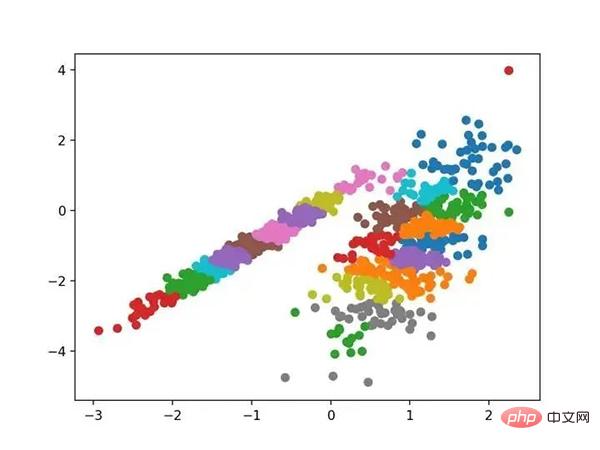
Scatterplot set data dengan kelompok dikenal pasti menggunakan perambatan perkaitan
Pengelompokan Agregat Melibatkan contoh penggabungan sehingga nombor yang dikehendaki kluster dicapai. Ia merupakan sebahagian daripada kelas kaedah pengelompokan hierarki yang lebih luas, dilaksanakan melalui kelas AgglomerationClustering, dan konfigurasi utama ialah set " n_clusters ", yang merupakan anggaran bilangan gugusan dalam data, cth. Contoh lengkap disenaraikan di bawah.
# 聚合聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import AgglomerativeClustering from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = AgglomerativeClustering(n_clusters=2) # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
Jalankan contoh agar sesuai dengan model pada set data latihan dan ramalkan kelompok untuk setiap contoh dalam set data. Plot berselerak kemudian dibuat, diwarnai oleh kelompok yang ditetapkan. Dalam kes ini, kumpulan yang munasabah boleh didapati.
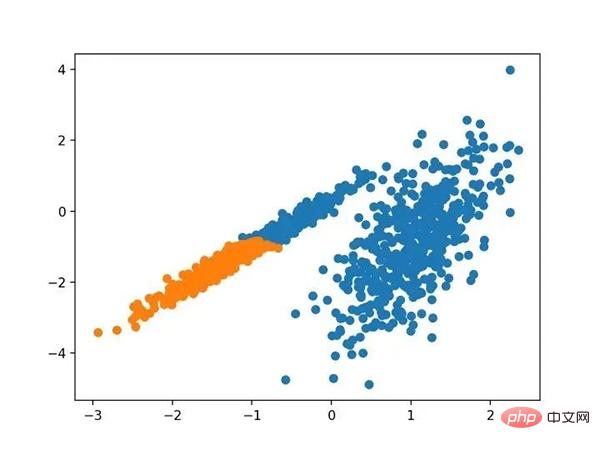
Petak serakan bagi set data dengan gugusan dikenal pasti menggunakan pengelompokan aglomeratif
BIRCH 聚类( BIRCH 是平衡迭代减少的缩写,聚类使用层次结构)包括构造一个树状结构,从中提取聚类质心。
它是通过 Birch 类实现的,主要配置是“ threshold ”和“ n _ clusters ”超参数,后者提供了群集数量的估计。下面列出了完整的示例。
# birch聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import Birch from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = Birch(threshold=0.01, n_clusters=2) # 适配模型 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,可以找到一个很好的分组。
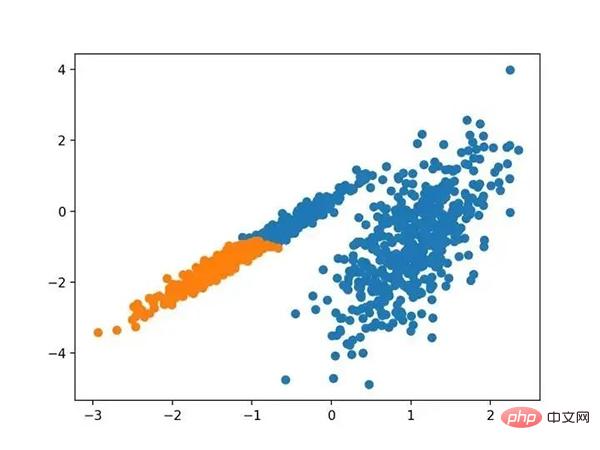
使用BIRCH聚类确定具有聚类的数据集的散点图
DBSCAN 聚类(其中 DBSCAN 是基于密度的空间聚类的噪声应用程序)涉及在域中寻找高密度区域,并将其周围的特征空间区域扩展为群集。
它是通过 DBSCAN 类实现的,主要配置是“ eps ”和“ min _ samples ”超参数。
下面列出了完整的示例。
# dbscan 聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import DBSCAN from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = DBSCAN(eps=0.30, min_samples=9) # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,尽管需要更多的调整,但是找到了合理的分组。
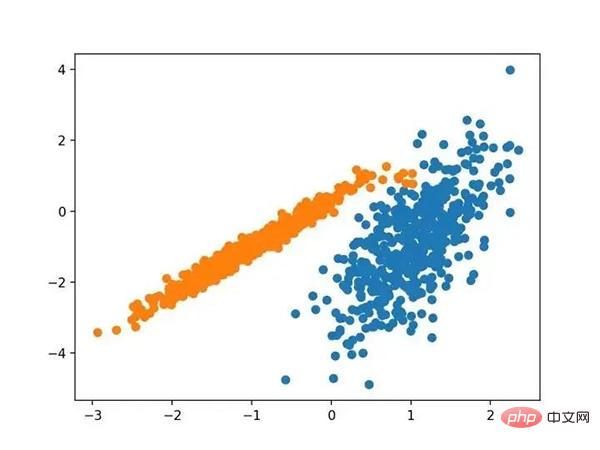
使用DBSCAN集群识别出具有集群的数据集的散点图
K-均值聚类可以是最常见的聚类算法,并涉及向群集分配示例,以尽量减少每个群集内的方差。
它是通过 K-均值类实现的,要优化的主要配置是“ n _ clusters ”超参数设置为数据中估计的群集数量。下面列出了完整的示例。
# k-means 聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import KMeans from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = KMeans(n_clusters=2) # 模型拟合 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,可以找到一个合理的分组,尽管每个维度中的不等等方差使得该方法不太适合该数据集。
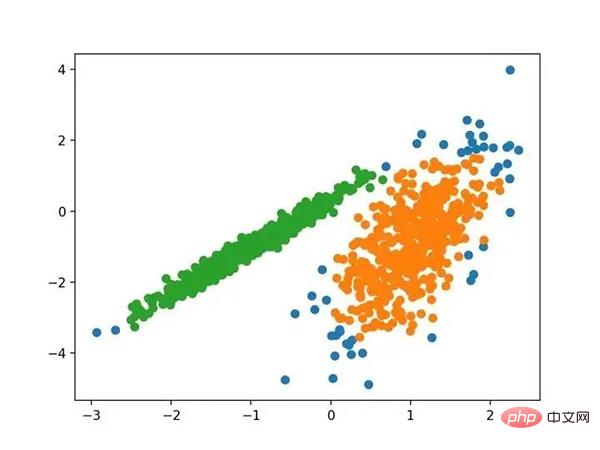
使用K均值聚类识别出具有聚类的数据集的散点图
Mini-Batch K-均值是 K-均值的修改版本,它使用小批量的样本而不是整个数据集对群集质心进行更新,这可以使大数据集的更新速度更快,并且可能对统计噪声更健壮。
它是通过 MiniBatchKMeans 类实现的,要优化的主配置是“ n _ clusters ”超参数,设置为数据中估计的群集数量。下面列出了完整的示例。
# mini-batch k均值聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import MiniBatchKMeans from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = MiniBatchKMeans(n_clusters=2) # 模型拟合 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,会找到与标准 K-均值算法相当的结果。
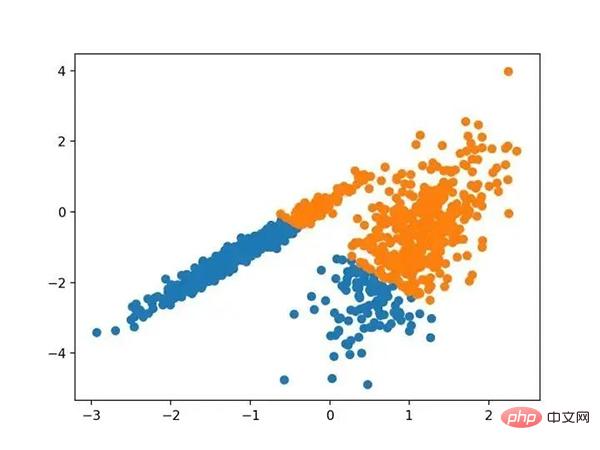
带有最小批次K均值聚类的聚类数据集的散点图
均值漂移聚类涉及到根据特征空间中的实例密度来寻找和调整质心。
它是通过 MeanShift 类实现的,主要配置是“带宽”超参数。下面列出了完整的示例。
# 均值漂移聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import MeanShift from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = MeanShift() # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,可以在数据中找到一组合理的群集。
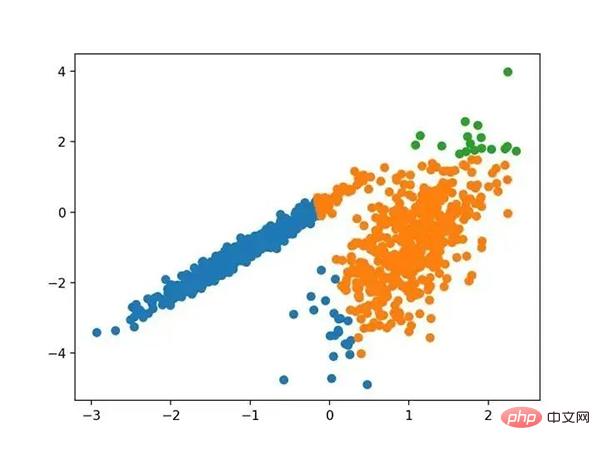
具有均值漂移聚类的聚类数据集散点图
OPTICS 聚类( OPTICS 短于订购点数以标识聚类结构)是上述 DBSCAN 的修改版本。
它是通过 OPTICS 类实现的,主要配置是“ eps ”和“ min _ samples ”超参数。下面列出了完整的示例。
# optics聚类 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import OPTICS from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = OPTICS(eps=0.8, min_samples=10) # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,我无法在此数据集上获得合理的结果。
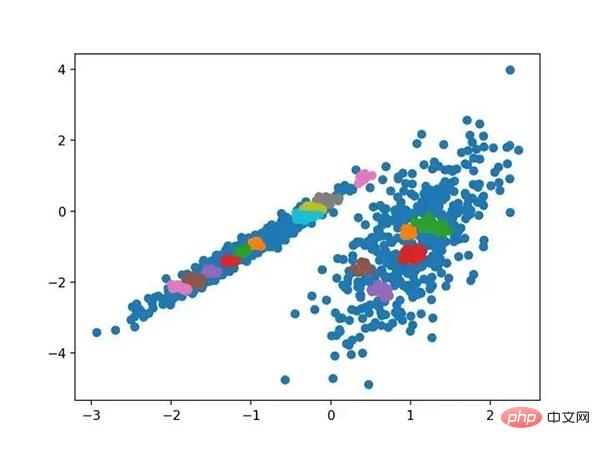
使用OPTICS聚类确定具有聚类的数据集的散点图
光谱聚类是一类通用的聚类方法,取自线性线性代数。
它是通过 Spectral 聚类类实现的,而主要的 Spectral 聚类是一个由聚类方法组成的通用类,取自线性线性代数。要优化的是“ n _ clusters ”超参数,用于指定数据中的估计群集数量。下面列出了完整的示例。
# spectral clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import SpectralClustering from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = SpectralClustering(n_clusters=2) # 模型拟合与聚类预测 yhat = model.fit_predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。
在这种情况下,找到了合理的集群。
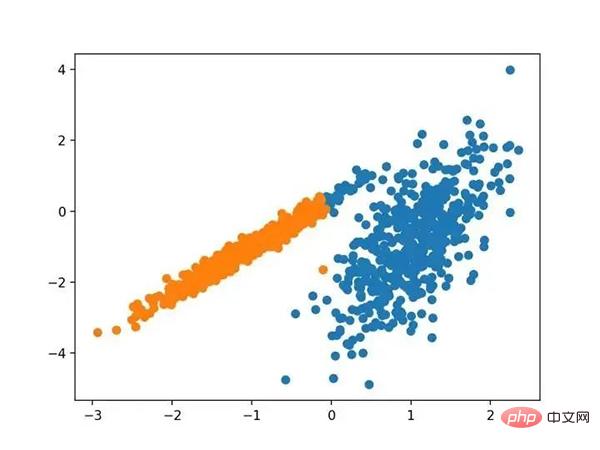
使用光谱聚类聚类识别出具有聚类的数据集的散点图
高斯混合模型总结了一个多变量概率密度函数,顾名思义就是混合了高斯概率分布。它是通过 Gaussian Mixture 类实现的,要优化的主要配置是“ n _ clusters ”超参数,用于指定数据中估计的群集数量。下面列出了完整的示例。
# 高斯混合模型 from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.mixture import GaussianMixture from matplotlib import pyplot # 定义数据集 X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # 定义模型 model = GaussianMixture(n_components=2) # 模型拟合 model.fit(X) # 为每个示例分配一个集群 yhat = model.predict(X) # 检索唯一群集 clusters = unique(yhat) # 为每个群集的样本创建散点图 for cluster in clusters: # 获取此群集的示例的行索引 row_ix = where(yhat == cluster) # 创建这些样本的散布 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 绘制散点图 pyplot.show()
运行该示例符合训练数据集上的模型,并预测数据集中每个示例的群集。然后创建一个散点图,并由其指定的群集着色。在这种情况下,我们可以看到群集被完美地识别。这并不奇怪,因为数据集是作为 Gaussian 的混合生成的。
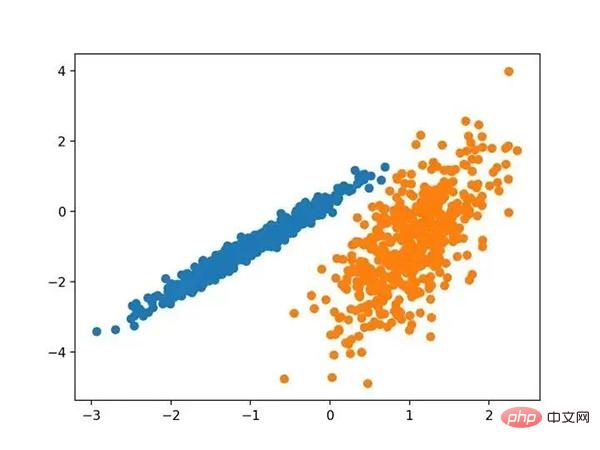
使用高斯混合聚类识别出具有聚类的数据集的散点图
在本教程中,您发现了如何在 python 中安装和使用顶级聚类算法。具体来说,你学到了:
Atas ialah kandungan terperinci Lengkapkan contoh operasi Python untuk sepuluh algoritma pengelompokan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




