Enam algoritma pengelompokan yang mesti diketahui oleh saintis data

Pada masa ini, banyak aplikasi seperti Google News menggunakan algoritma pengelompokan sebagai kaedah pelaksanaan utama mereka boleh menggunakan sejumlah besar data tidak berlabel untuk membina pengelompokan topik yang hebat. Artikel ini memperkenalkan 6 jenis kaedah arus perdana daripada pengelompokan K-means yang paling asas kepada kaedah berasaskan kepadatan yang berkuasa Mereka masing-masing mempunyai bidang kepakaran dan senario mereka sendiri, dan idea asas tidak semestinya terhad kepada kaedah pengelompokan.

Artikel ini akan bermula dengan pengelompokan K-means yang mudah dan cekap, dan kemudian memperkenalkan pengelompokan anjakan min, pengelompokan berasaskan kepadatan, campuran Gaussian dan pengelompokan kaedah jangkaan maksimum, Pengelompokan hierarki dan pengesanan kumpulan graf digunakan pada data berstruktur. Kami bukan sahaja akan menganalisis konsep pelaksanaan asas, tetapi juga memberikan kelebihan dan kekurangan setiap algoritma untuk menjelaskan senario aplikasi sebenar.

Pengkelompokan ialah teknik pembelajaran mesin yang melibatkan pengumpulan titik data. Memandangkan satu set titik data, kita boleh menggunakan algoritma pengelompokan untuk mengklasifikasikan setiap titik data ke dalam kumpulan tertentu. Secara teori, titik data kepunyaan kumpulan yang sama harus mempunyai sifat dan/atau ciri yang serupa, manakala titik data kepunyaan kumpulan berbeza harus mempunyai sifat dan/atau ciri yang sangat berbeza. Pengelompokan ialah kaedah pembelajaran tanpa pengawasan dan teknik analisis data statistik yang biasa digunakan dalam banyak bidang.

K-Means (K-Means) Pengelompokan

K-Means mungkin merupakan algoritma pengelompokan yang paling terkenal. Ia adalah sebahagian daripada banyak kursus pengenalan sains data dan pembelajaran mesin. Sangat mudah untuk difahami dan dilaksanakan dalam kod! Sila lihat gambar di bawah.

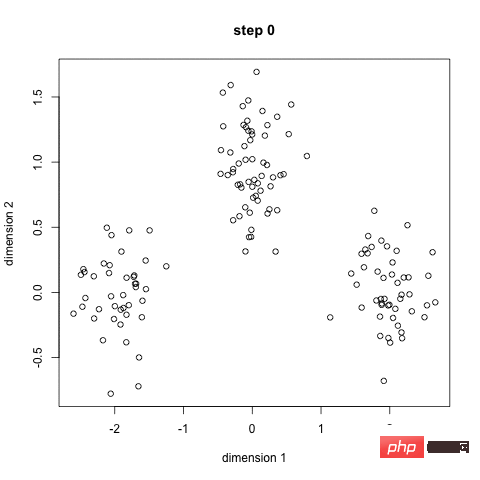
K-Means Clustering

Mula-mula, kami memilih beberapa kelas/kumpulan dan secara rawak memulakan titik tengah masing-masing. Untuk menentukan bilangan kelas untuk digunakan, adalah idea yang baik untuk melihat data dengan cepat dan cuba mengenal pasti kumpulan yang berbeza. Titik tengah ialah lokasi dengan panjang yang sama dengan setiap vektor titik data, iaitu "X" dalam imej di atas.

Kelaskan setiap titik dengan mengira jarak antara titik data dan pusat setiap kumpulan, dan kemudian kelaskan titik itu ke dalam kumpulan yang paling hampir dengan pusat kumpulan itu.

Berdasarkan titik pengelasan ini, kami mengira semula pusat kumpulan menggunakan min semua vektor dalam kumpulan.

Ulang langkah ini untuk bilangan lelaran tertentu, atau sehingga pusat kumpulan berubah sedikit selepas setiap lelaran. Anda juga boleh memilih untuk memulakan pusat kumpulan secara rawak beberapa kali dan kemudian memilih larian yang nampaknya memberikan hasil terbaik.

K-Means mempunyai kelebihan kerana pantas, kerana apa yang kita lakukan sebenarnya ialah mengira jarak antara titik dan pusat kumpulan: pengiraan yang sangat sedikit! Jadi ia mempunyai kerumitan linear O(n).

K-Means pula mempunyai beberapa kelemahan. Pertama, anda perlu memilih berapa banyak kumpulan/kelas yang ada. Ini tidak selalu dilakukan dengan berhati-hati, dan secara idealnya kami mahu algoritma pengelompokan membantu kami menyelesaikan masalah bilangan kelas untuk dikelaskan, kerana tujuannya adalah untuk mendapatkan beberapa cerapan daripada data. K-means juga bermula dari pusat kluster yang dipilih secara rawak, jadi ia mungkin menghasilkan hasil kluster yang berbeza dalam algoritma yang berbeza. Oleh itu, keputusan mungkin tidak boleh dihasilkan semula dan kurang konsisten. Kaedah pengelompokan lain lebih konsisten.

K-Medians ialah satu lagi algoritma pengelompokan yang berkaitan dengan K-Means, kecuali daripada menggunakan min, pusat kumpulan dikira semula menggunakan vektor median kumpulan. Kaedah ini tidak sensitif kepada outlier (kerana median digunakan), tetapi jauh lebih perlahan untuk set data yang lebih besar kerana pengisihan diperlukan pada setiap lelaran semasa mengira vektor median.

Pengkelompokan Shift Min

Pengkelompokan Anjakan Min ialah algoritma berasaskan tetingkap gelongsor yang cuba mencari kawasan padat titik data. Ini adalah algoritma berasaskan centroid, yang bermaksud matlamatnya adalah untuk mencari titik tengah setiap kumpulan/kelas, yang dicapai dengan mengemas kini titik calon titik tengah kepada min titik dalam tetingkap gelongsor. Tetingkap calon ini kemudiannya ditapis dalam peringkat pasca pemprosesan untuk menghapuskan hampir duplikasi, membentuk set akhir titik tengah dan kumpulan yang sepadan. Sila lihat lagenda di bawah.

Pengkelompokan anjakan min untuk satu tetingkap gelongsor

1. Untuk menerangkan anjakan min, kami akan mempertimbangkan satu set titik dalam ruang dua dimensi seperti yang ditunjukkan dalam rajah di atas. Kita mulakan dengan tetingkap gelongsor bulat berpusat pada titik C (dipilih secara rawak) dan dengan teras jejari r. Anjakan min ialah algoritma mendaki bukit yang melibatkan pergerakan berulang ke arah kawasan berketumpatan lebih tinggi pada setiap langkah sehingga penumpuan.
2. Dalam setiap lelaran, tetingkap gelongsor bergerak ke arah kawasan ketumpatan yang lebih tinggi dengan menggerakkan titik tengah ke arah min titik dalam tetingkap (oleh itu namanya). Ketumpatan dalam tetingkap gelongsor adalah berkadar dengan bilangan titik di dalamnya. Sememangnya, dengan bergerak ke arah min titik dalam tetingkap, ia secara beransur-ansur bergerak ke arah kawasan yang mempunyai ketumpatan titik yang lebih tinggi.
3. Kami terus mengalihkan tetingkap gelongsor mengikut min sehingga tiada arah yang boleh menampung lebih banyak titik dalam kernel. Lihat gambar di atas; kami terus menggerakkan bulatan sehingga ketumpatan tidak lagi meningkat (iaitu bilangan titik dalam tetingkap).
4. Proses langkah 1 hingga 3 diselesaikan melalui banyak tingkap gelongsor sehingga semua titik terletak dalam satu tetingkap. Apabila berbilang tetingkap gelongsor bertindih, tetingkap yang mengandungi mata terbanyak dikekalkan. Kemudian pengelompokan dilakukan berdasarkan tetingkap gelongsor di mana titik data berada.

Keseluruhan proses dari awal hingga akhir untuk semua tingkap gelongsor ditunjukkan di bawah. Setiap titik hitam mewakili centroid tetingkap gelongsor, dan setiap titik kelabu mewakili titik data.

Keseluruhan proses pengelompokan anjakan min

Berbanding dengan pengelompokan K-means, kaedah ini tidak perlu memilih bilangan kelompok kerana anjakan min secara automatik Temui ini. Ini adalah kelebihan yang besar. Hakikat bahawa kluster memusatkan kluster ke arah ketumpatan titik maksimum juga sangat memuaskan, kerana ia sangat intuitif untuk memahami dan menyesuaikan diri dengan implikasi yang dipacu data semula jadi. Kelemahannya ialah pilihan saiz/radius tetingkap "r" mungkin tidak penting.

Kaedah pengelompokan berasaskan ketumpatan (DBSCAN)

DBSCAN ialah algoritma pengelompokan berasaskan ketumpatan yang serupa dengan anjakan min tetapi mempunyai beberapa kelebihan ketara. Lihat satu lagi grafik yang menyeronokkan di bawah dan mari mulakan!

Pengkelompokan DBSCAN

1. DBSCAN bermula dari titik data permulaan sewenang-wenangnya yang belum dilawati lagi. Kejiranan titik ini diekstrak dengan jarak ε (semua titik dalam jarak ε ialah titik jiran).
2. Jika terdapat bilangan mata yang mencukupi dalam kejiranan ini (mengikut minPoints), proses pengelompokan bermula dan titik data semasa menjadi titik pertama bagi kelompok baharu. Jika tidak, titik akan ditandakan sebagai hingar (kemudian titik hingar ini mungkin masih menjadi sebahagian daripada kelompok). Dalam kedua-dua kes, titik ditandakan sebagai "Dilawati".
3. Untuk titik pertama dalam kluster baharu, titik dalam kejiranan jarak εnya juga menjadi sebahagian daripada kluster. Proses menjadikan semua titik dalam kejiranan ε tergolong dalam kelompok yang sama diulang untuk semua titik baharu yang baru ditambahkan pada kelompok.
4. Ulang langkah 2 dan 3 sehingga semua titik dalam kelompok dikenal pasti, iaitu semua titik dalam kejiranan ε kelompok telah dilawati dan ditanda.
5. Setelah kami selesai dengan kluster semasa, titik baru yang belum dilawati akan diambil dan diproses, mengakibatkan penemuan kluster atau bunyi lain. Proses ini diulang sehingga semua titik ditanda sebagai dilawati. Memandangkan semua titik telah dilawati, setiap titik tergolong dalam kumpulan atau bunyi bising.

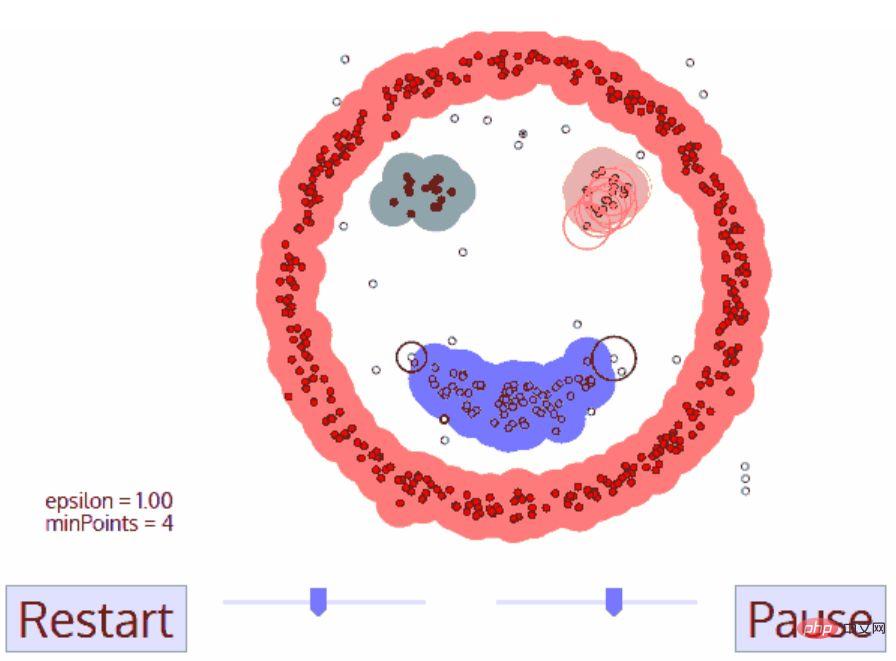
DBSCAN mempunyai banyak kelebihan berbanding algoritma pengelompokan lain. Pertama, ia tidak memerlukan bilangan kluster yang tetap sama sekali. Ia juga mengenal pasti outlier sebagai hingar, tidak seperti anjakan min, yang hanya mengumpulkan titik data ke dalam kelompok walaupun ia sangat berbeza. Selain itu, ia mampu mencari kluster dari sebarang saiz dan bentuk dengan baik.

Kelemahan utama DBSCAN ialah ia tidak berfungsi sebaik algoritma pengelompokan lain apabila ketumpatan kelompok berbeza. Ini kerana tetapan ambang jarak ε dan minPoints yang digunakan untuk mengenal pasti titik kejiranan akan berubah dengan kelompok apabila ketumpatan berubah. Kelemahan ini juga timbul dalam data berdimensi sangat tinggi, kerana ambang jarak ε sekali lagi menjadi sukar untuk dianggarkan.

Pengelompokkan Maksimum Jangkaan (EM) dengan Model Campuran Gaussian (GMM)

Kelemahan utama K-Means ialah penggunaan kaedah pusat kluster yang mudah. Daripada rajah di bawah, kita dapat melihat mengapa ini bukan pendekatan terbaik. Di sebelah kiri, anda boleh melihat dengan jelas bahawa terdapat dua kelompok bulat dengan jejari berbeza, berpusat pada min yang sama. K-Means tidak dapat menangani keadaan ini kerana cara kluster ini sangat dekat. K-Means juga gagal dalam kes di mana kluster tidak bulat, sekali lagi kerana menggunakan min sebagai pusat kluster.

Dua Kes Kegagalan K-Means

Model Campuran Gaussian (GMM) memberi kita lebih fleksibiliti daripada K-Means. Untuk GMM, kami menganggap bahawa titik data adalah diedarkan Gaussian ini adalah andaian yang kurang ketat daripada menggunakan min untuk menganggap bahawa ia adalah bulat. Dengan cara ini, kita mempunyai dua parameter untuk menerangkan bentuk kelompok: min dan sisihan piawai! Mengambil 2D sebagai contoh, ini bermakna gugusan boleh mengambil sebarang bentuk bentuk elips (memandangkan kita mempunyai sisihan piawai dalam kedua-dua arah x dan y). Oleh itu, setiap taburan Gaussian ditugaskan kepada satu kelompok.

Untuk mencari parameter Gaussian (seperti min dan sisihan piawai) setiap kelompok, kami akan menggunakan algoritma pengoptimuman yang dipanggil Expectation Maximum (EM). Lihat rajah di bawah, yang merupakan contoh kesesuaian Gaussian dengan gugusan. Kami kemudiannya boleh meneruskan proses pengelompokan jangkaan maksimum menggunakan GMM.

Pengkelompokan EM menggunakan GMM

1. Kami mula-mula memilih bilangan kelompok (seperti yang dilakukan oleh K-Means) dan secara rawak memulakan setiap parameter pengedaran Gaussian daripada kelompok. Anda juga boleh cuba memberikan tekaan yang baik untuk parameter awal dengan melihat cepat pada data. Walau bagaimanapun, ambil perhatian bahawa seperti yang anda lihat di atas ini tidak 100% perlu kerana Gaussian memulakan kita dengan sangat lemah tetapi dengan cepat dioptimumkan.
2. Memandangkan taburan Gaussian bagi setiap gugusan, hitung kebarangkalian bahawa setiap titik data tergolong dalam gugusan tertentu. Semakin dekat satu titik dengan pusat Gaussian, semakin besar kemungkinan ia tergolong dalam kelompok itu. Ini sepatutnya intuitif kerana dengan pengedaran Gaussian kita menganggap bahawa kebanyakan data lebih dekat dengan pusat kluster.
3. Berdasarkan kebarangkalian ini, kami mengira set parameter taburan Gaussian baharu yang memaksimumkan kebarangkalian titik data dalam kelompok. Kami mengira parameter baharu ini menggunakan jumlah wajaran lokasi titik data, dengan berat ialah kebarangkalian titik data itu tergolong dalam kelompok tertentu itu. Untuk menerangkannya secara visual, kita boleh lihat pada gambar di atas, terutamanya gugusan kuning, yang kita gunakan sebagai contoh. Pengedaran bermula serta-merta pada lelaran pertama, tetapi kita dapat melihat bahawa kebanyakan titik kuning berada di sebelah kanan pengedaran. Apabila kita mengira jumlah wajaran kebarangkalian, walaupun terdapat beberapa titik berhampiran pusat, ia kebanyakannya berada di sebelah kanan. Oleh itu, purata taburan secara semula jadi akan hampir dengan titik ini. Kita juga dapat melihat bahawa kebanyakan titik diedarkan "dari kanan atas ke kiri bawah". Oleh itu sisihan piawai diubah untuk mencipta elips yang lebih sesuai dengan mata untuk memaksimumkan jumlah wajaran kebarangkalian.
4. Ulang langkah 2 dan 3 sehingga penumpuan, di mana taburan berubah sedikit antara lelaran.

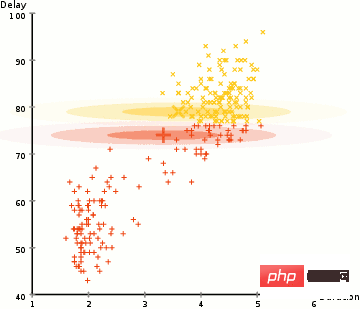
Terdapat dua kelebihan utama untuk menggunakan GMM. Pertama, GMM lebih fleksibel daripada K-Means dari segi kovarians kelompok kerana parameter sisihan piawai, kelompok boleh mengambil bentuk elips dan bukannya terhad kepada bulatan. K-Means sebenarnya adalah kes khas GMM, di mana kovarians setiap kluster menghampiri 0 dalam semua dimensi. Kedua, kerana GMM menggunakan kebarangkalian, boleh terdapat banyak kelompok bagi setiap titik data. Jadi jika titik data berada di tengah-tengah dua kelompok bertindih, kita boleh menentukan kelasnya hanya dengan mengatakan bahawa X peratus daripadanya tergolong dalam kelas 1 dan Y peratus kepada kelas 2. Iaitu, GMM menyokong kelayakan hibrid.

Kelompok Hierarki Agglomeratif

Algoritma pengelompokan hierarki sebenarnya dibahagikan kepada dua kategori: atas ke bawah atau bawah ke atas. Algoritma bawah ke atas mula-mula merawat setiap titik data sebagai gugusan tunggal dan kemudian menggabungkan (atau mengagregat) dua gugusan berturut-turut sehingga semua gugusan digabungkan menjadi satu gugusan yang mengandungi semua titik data. Oleh itu, pengelompokan hierarki bawah ke atas dipanggil pengelompokan hierarki aglomeratif atau HAC. Hierarki kelompok ini diwakili oleh pokok (atau dendrogram). Akar pokok adalah satu-satunya kelompok yang mengumpul semua sampel, dan daun adalah kelompok dengan hanya satu sampel. Sebelum pergi ke langkah algoritma, sila lihat legenda di bawah.

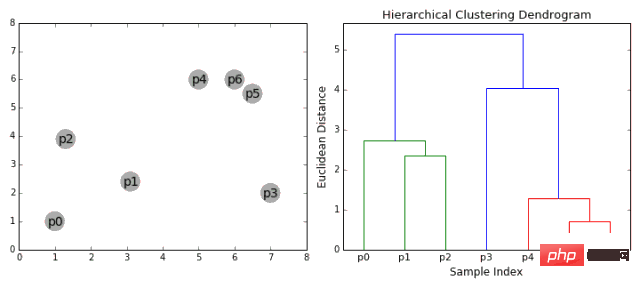
Penghimpunan hierarki aglomeratif

1. Kami mula-mula menganggap setiap titik data sebagai gugusan tunggal, iaitu jika kami mempunyai titik data X dalam set data kami, maka kami mempunyai gugusan X. Kami kemudian memilih metrik jarak yang mengukur jarak antara dua kelompok. Sebagai contoh, kami akan menggunakan kaitan purata, yang mentakrifkan jarak antara dua kluster sebagai jarak purata antara titik data dalam kluster pertama dan titik data dalam kluster kedua.
2. Dalam setiap lelaran, kami menggabungkan dua gugusan menjadi satu. Kedua-dua kluster yang akan digabungkan harus mempunyai kaitan purata terkecil. Iaitu, mengikut metrik jarak yang kami pilih, kedua-dua kelompok mempunyai jarak terkecil antara mereka dan oleh itu adalah yang paling serupa dan harus digabungkan bersama.
3. Ulang langkah 2 sehingga kita mencapai akar pokok, iaitu kita hanya mempunyai satu gugusan yang mengandungi semua titik data. Dengan cara ini, kita hanya perlu memilih bila hendak menghentikan penggabungan kelompok, iaitu bila hendak berhenti membina pokok, untuk memilih berapa banyak kelompok yang kita perlukan pada akhirnya!

Pengelompokan hierarki tidak memerlukan kita menyatakan bilangan gugusan, malah kita boleh memilih bilangan gugusan yang mana kelihatan paling baik memandangkan kita sedang membina pokok. Selain itu, algoritma tidak sensitif kepada pilihan metrik jarak, semuanya berprestasi sama baik, manakala bagi algoritma pengelompokan lain, pilihan metrik jarak adalah penting. Contoh kaedah pengelompokan hierarki yang sangat baik ialah apabila data asas mempunyai struktur hierarki dan anda ingin memulihkan hierarki algoritma pengelompokan lain tidak boleh melakukan ini. Tidak seperti kerumitan linear K-Means dan GMM, kelebihan pengelompokan hierarki ini datang pada kos kecekapan yang lebih rendah kerana ia mempunyai kerumitan masa O(n³).

Graf Komuniti Pengesanan

Apabila data kami boleh diwakili sebagai rangkaian atau graf, kami boleh menggunakan kaedah pengesanan komuniti graf untuk melengkapkan pengelompokan. Dalam algoritma ini, komuniti graf biasanya ditakrifkan sebagai subset bucu yang bersambung lebih rapat daripada bahagian lain rangkaian.

Mungkin kes yang paling intuitif ialah rangkaian sosial. Bucu mewakili orang, dan tepi yang menghubungkan bucu mewakili pengguna yang merupakan rakan atau peminat. Walau bagaimanapun, untuk memodelkan sistem sebagai rangkaian, kita mesti mencari cara untuk menyambungkan pelbagai komponen dengan cekap. Beberapa aplikasi inovatif teori graf untuk pengelompokan termasuk pengekstrakan ciri data imej, analisis rangkaian pengawalseliaan gen, dsb.

Di bawah ialah rajah ringkas yang menunjukkan 8 tapak web yang dilihat baru-baru ini, disambungkan berdasarkan pautan dari halaman Wikipedia mereka.

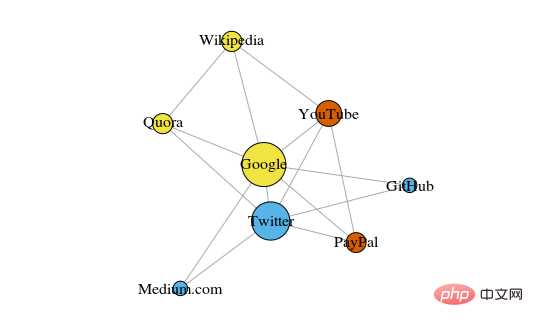
Warna bucu ini menunjukkan perhubungan kumpulannya dan saiz ditentukan berdasarkan pusatnya. Kelompok ini juga masuk akal dalam kehidupan sebenar, di mana bucu kuning biasanya merupakan tapak rujukan/carian dan bucu biru adalah semua tapak penerbitan dalam talian (artikel, tweet atau kod).

Andaikan kita telah mengelompokkan rangkaian ke dalam kumpulan. Kami kemudiannya boleh menggunakan skor modulariti ini untuk menilai kualiti pengelompokan. Skor yang lebih tinggi bermakna kami membahagikan rangkaian kepada kumpulan "tepat", manakala skor rendah bermakna pengelompokan kami lebih hampir kepada rawak. Seperti yang ditunjukkan dalam rajah di bawah:

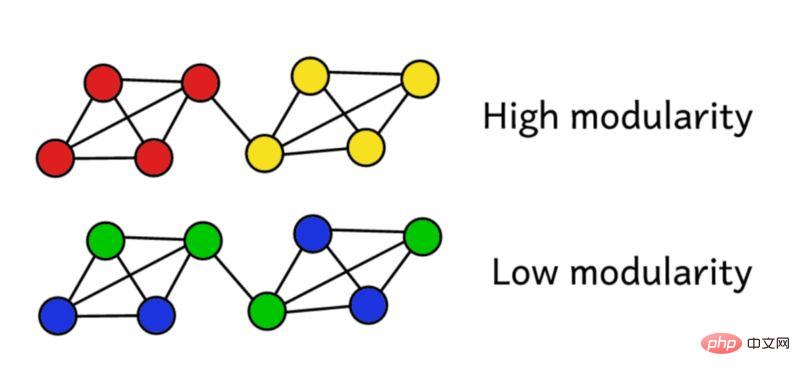
Modulariti boleh dikira menggunakan formula berikut:

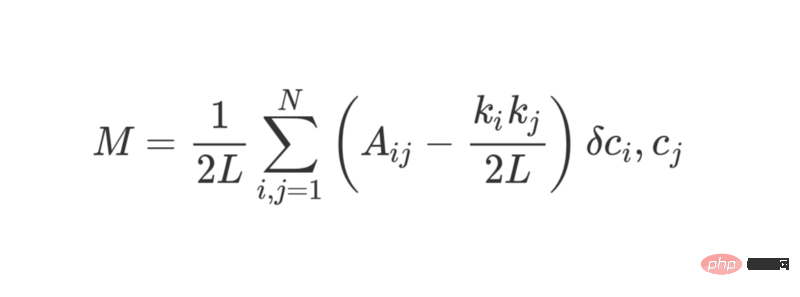
di mana L mewakili tepi dalam rangkaian Kuantiti, k_i dan k_j merujuk kepada darjah setiap bucu, yang boleh didapati dengan menjumlahkan sebutan bagi setiap baris dan lajur. Mendarab dua dan membahagi dengan 2L mewakili jangkaan bilangan tepi antara bucu i dan j apabila rangkaian ditugaskan secara rawak.

Secara keseluruhan, istilah dalam kurungan mewakili perbezaan antara struktur sebenar rangkaian dan struktur yang dijangkakan apabila digabungkan secara rawak. Mengkaji nilainya menunjukkan bahawa ia mengembalikan nilai tertinggi apabila A_ij = 1 dan ( k_i k_j ) / 2L adalah kecil. Ini bermakna apabila terdapat kelebihan "tidak dijangka" antara titik tetap i dan j, nilai yang terhasil adalah lebih tinggi.

δc_i yang terakhir, c_j ialah fungsi Kronecker δ yang terkenal (fungsi Kronecker-delta). Berikut ialah penjelasan Pythonnya:

Kemodulatan graf boleh dikira melalui formula di atas, dan lebih tinggi modulariti, lebih baik tahap rangkaian dikelompokkan ke dalam kumpulan yang berbeza. Oleh itu, cara terbaik untuk mengelompokkan rangkaian boleh didapati dengan mencari modulariti maksimum melalui kaedah pengoptimuman.

Kombinatorik memberitahu kita bahawa untuk rangkaian dengan hanya 8 bucu, terdapat 4140 kaedah pengelompokan yang berbeza. Rangkaian 16 bucu akan dikelompokkan dalam lebih 10 bilion cara. Kaedah pengelompokan yang mungkin bagi rangkaian dengan 32 bucu akan melebihi 128 septillion (10^21); jika rangkaian anda mempunyai 80 bucu, bilangan kaedah pengelompokan yang mungkin telah melebihi bilangan kaedah pengelompokan dalam alam semesta yang boleh diperhatikan.

Oleh itu, kita mesti menggunakan heuristik yang berfungsi dengan baik dalam menilai kelompok yang menghasilkan skor modulariti tertinggi, tanpa mencuba setiap kemungkinan. Ini ialah algoritma yang dipanggil Fast-Greedy Modularity-Maximization, yang agak serupa dengan algoritma pengelompokan hierarki aglomeratif yang diterangkan di atas. Cuma Mod-Max tidak menggabungkan kumpulan berdasarkan jarak, tetapi menggabungkan kumpulan berdasarkan perubahan dalam modulariti.

Begini cara ia berfungsi:

• Mula-mula pada mulanya tetapkan setiap bucu kepada kumpulannya sendiri, kemudian kirakan modulariti M bagi keseluruhan rangkaian.
• Langkah 1 memerlukan setiap pasangan komuniti dipautkan oleh sekurang-kurangnya satu pautan unilateral Jika dua komuniti bergabung bersama, algoritma mengira perubahan modulariti yang terhasil ΔM.
• Langkah kedua ialah memilih pasangan kumpulan dengan peningkatan terbesar dalam ΔM dan kemudian menggabungkannya. Satu modulariti baru M kemudiannya dikira untuk kelompok ini dan direkodkan.
• Ulang langkah 1 dan 2 - setiap kali menggabungkan pasangan kumpulan supaya anda mendapat keuntungan maksimum ΔM, kemudian rekod corak pengelompokan baharu dan skor modulariti sepadannya M.
• Anda boleh berhenti apabila semua bucu telah dikumpulkan menjadi satu gugusan gergasi. Algoritma kemudian memeriksa rekod dalam proses ini dan mencari corak pengelompokan di mana nilai M tertinggi telah dikembalikan. Ini ialah struktur kumpulan yang dikembalikan.

Pengesanan komuniti ialah bidang penyelidikan yang popular dalam teori graf Keterbatasannya ditunjukkan terutamanya dalam fakta bahawa ia mengabaikan beberapa kelompok kecil dan hanya terpakai pada model graf berstruktur. Walau bagaimanapun, jenis algoritma ini mempunyai prestasi yang sangat baik dalam data berstruktur biasa dan data rangkaian sebenar.

Kesimpulan

Di atas ialah 6 algoritma pengelompokan utama yang perlu diketahui oleh saintis data! Kami akan menamatkan artikel ini dengan menunjukkan visualisasi pelbagai algoritma!

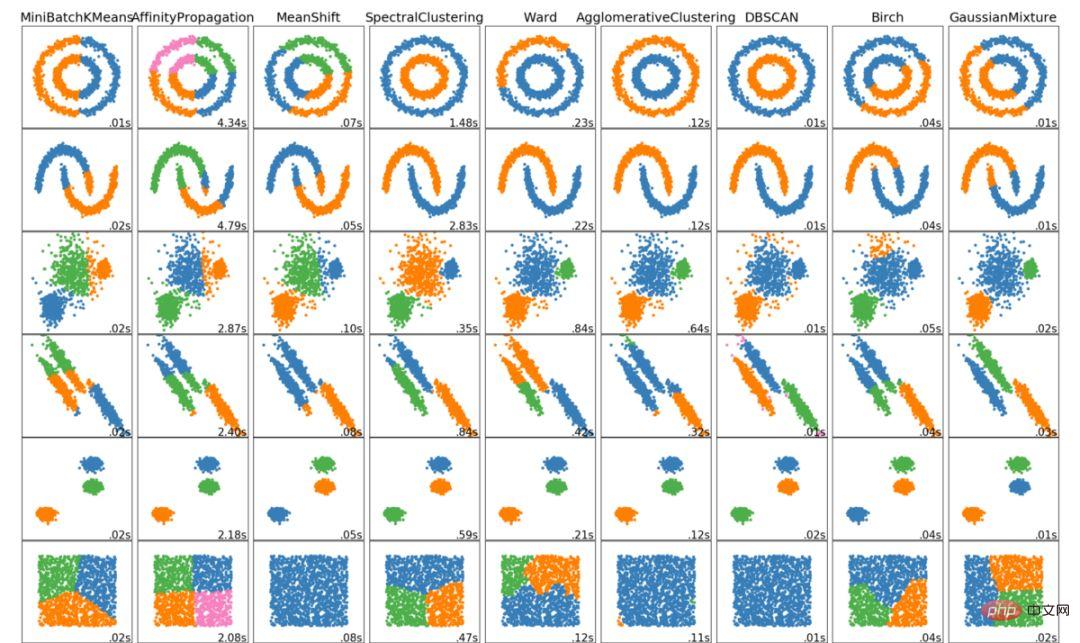
Atas ialah kandungan terperinci Enam algoritma pengelompokan yang mesti diketahui oleh saintis data. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!