
Dalam beberapa tahun kebelakangan ini, bidang kecerdasan buatan semakin mengkritik mekanisme semakan persidangan komputer berskala besar Percanggahan di sebalik semua ini berpunca daripada kepentingan pengarang kertas, penganjur persidangan dan penyemak yang tidak konsisten:
Pautan dokumen : https: //docs.google.com/document/d/1j7Mn2ZkquSzWJ_EzxdXBP3z_JQtrSeUa-CQ0gotAuYw/mobilebasic

Sebilangan besar kertas akan ditolak setiap tahun (kadar penerimaan persidangan kecerdasan buatan teratas seperti NeurIPS adalah kurang daripada 30% sepanjang tahun) , dan kebanyakan kertas kerja ini akan ditolak dengan hanya Menyertai penyerahan semula dengan pelarasan kecil atau malah tiada perubahan langsung akan sentiasa diterima oleh persidangan atau persidangan yang sama pada tahap yang sama. Memandangkan kebanyakan kertas kerja akhirnya akan diterima, mengapa tidak menurunkan ambang penerimaan supaya lebih banyak kertas boleh diterima selepas lebih sedikit penyerahan semula? Ini akan menghalang kertas yang sama daripada dibaca berulang kali oleh pengulas dan mengurangkan tekanan semakan.
Walaupun idea ini kelihatan sangat munasabah, penulis artikel ini mencadangkan untuk menggunakan model teori permainan untuk huraikan penulis dan pertemuan itu dan memberikan jawapan negatif kepada idea ini. Kertas penyelidikan telah diterima oleh Economics and Computation (2022). Di bawah model ini, artikel ini membincangkan prestasi mekanisme semakan dan membuat keputusan yang berbeza dalam menimbang kualiti mesyuarat dan tekanan semakan, seperti isu berikut:
 Cara menentukan ambang penerimaan Cemerlang terbaik?
Cara menentukan ambang penerimaan Cemerlang terbaik?
Adakah bilangan penyemak di atas kertas perlu ditambah?
Pertama, setiap pengarang mempunyai kertas kerja sedia untuk diserahkan. Dalam setiap pusingan penyerahan, pengarang membuat satu daripada dua keputusan: menyerahkan kertas itu ke persidangan teratas atau pertaruhan pasti (seperti persidangan kategori kedua yang kurang berprestij). Keputusan penyerahan ke persidangan IM dan pastinya bergantung pada mekanisme semakan dan kualiti kertas:
IM akan mempunyai kebarangkalian tertentu untuk menerima kertas tersebut diterima, penulis akan menerima faedah yang lebih besar ;pasti pertaruhan menjamin bahawa kertas itu akan diterima, tetapi faedahnya akan lebih kecil.
2. Kesimpulan utama
Menggunakan kaedah pemodelan di atas, kertas kerja ini menarik beberapa. kesimpulan Kesimpulan penting, termasuk:
1) Strategi optimum pengarang
Dalam model yang dipermudahkan (lihat teks asal untuk model yang lebih kompleks), artikel ini menjadikan Perkara berikut andaian dibuat: pengarang mengetahui kualiti sebenar kertas kerja mereka, keputusan persidangan tidak dapat diingati (keputusan untuk setiap pusingan semakan hanya bergantung pada pendapat penyemak dalam pusingan itu), dan pengarang mempunyai peluang penyerahan semula tanpa had. Dalam kes ini, pengarang mempunyai strategi optimum ambang:
Biasanya ambang penyerahan pengarang Θ adalah lebih rendah daripada ambang penerimaan persidangan τ, seperti yang ditunjukkan dalam rajah di bawah.
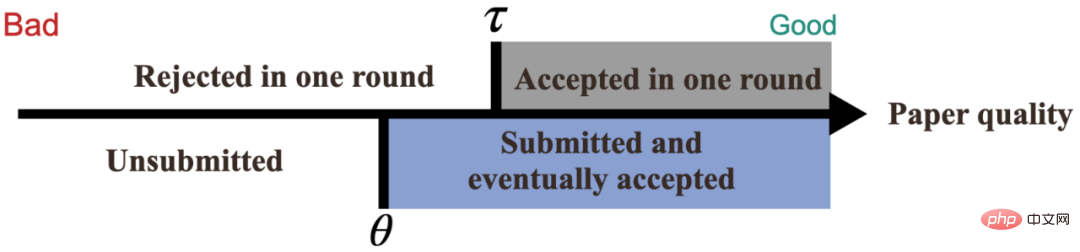
Kesimpulan di atas boleh digunakan untuk menerangkan paradoks penyerahan semula: mengapa menerima lebih banyak kertas kerja pada dasarnya tidak boleh Mengurangkan semakan tekanan? Ini kerana menurunkan ambang penerimaan persidangan τ pada masa yang sama akan menurunkan ambang penyerahan pengarang Θ, dengan itu menarik lebih banyak penyerahan kertas berkualiti rendah. Seperti yang ditunjukkan dalam rajah di bawah, jika ambang penerimaan diturunkan, beberapa kertas (kawasan ungu) yang sebelum ini dipilih untuk diserahkan ke persidangan kategori kedua kini dipilih untuk diserahkan ke persidangan teratas.
2) Kualiti mesyuarat dan tekanan semakan
Mekanisme semakan/membuat keputusan mesyuarat tertinggi perlu timbang kualiti mesyuarat Dan tekanan semak, anda tidak boleh mempunyai kedua-duanya.
Menukar ambang penerimaan akan mengubah kedua-dua kualiti mesyuarat dan tekanan ulasan (seperti yang ditunjukkan di bawah).
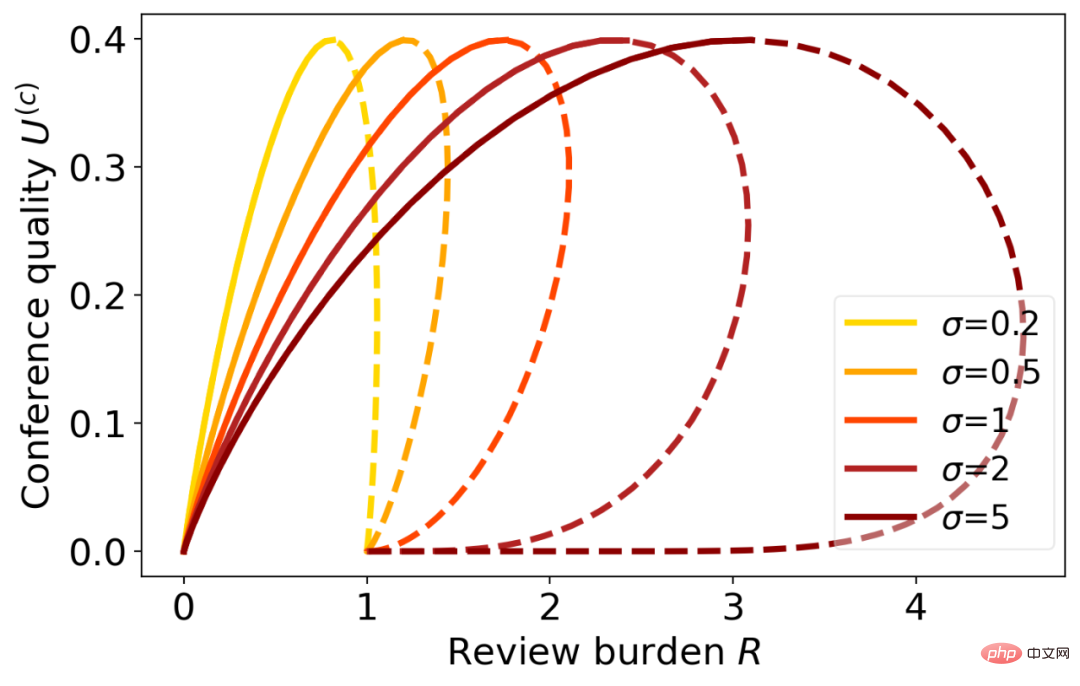
Gambar menunjukkan hubungan antara kualiti bertemu (ordinat) dan tekanan semakan (abscissa) mengenai penerimaan ambang Tukar keluk, σ ialah sisihan piawai hingar pengulas.
Tiga situasi berikut boleh membawa kepada pertukaran yang lebih baik antara kualiti pertemuan dan tekanan semakan (kualiti mesyuarat yang sama memerlukan tekanan semakan yang kurang):
Atas ialah kandungan terperinci Patutkah Dinghui menurunkan ambang penerimaan? Gunakan teori permainan untuk meneroka semakan optimum dan mekanisme membuat keputusan. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Apakah syiling NFT?
Apakah syiling NFT?
 Kaedah pelaksanaan fungsi benteng js
Kaedah pelaksanaan fungsi benteng js
 Bagaimana untuk menutup selepas menjalankan arahan nohup
Bagaimana untuk menutup selepas menjalankan arahan nohup
 Bagaimana untuk menukar antara lebar penuh dan separuh lebar
Bagaimana untuk menukar antara lebar penuh dan separuh lebar
 Kaedah analisis data
Kaedah analisis data
 Apakah perbezaan antara rabbitmq dan kafka
Apakah perbezaan antara rabbitmq dan kafka
 apakah julat python
apakah julat python
 keperluan konfigurasi perkakasan pelayan web
keperluan konfigurasi perkakasan pelayan web




