
Sepanjang kerjaya kejuruteraan perisian anda, anda mungkin menghadapi sekeping kod yang berprestasi buruk, mengambil masa yang lebih lama daripada yang boleh diterima. Lebih memburukkan lagi keadaan, prestasinya tidak konsisten dan agak berubah-ubah merentas pelbagai pelaksanaan.
Pada masa ini, anda perlu menerima bahawa apabila ia berkaitan dengan prestasi perisian, terdapat banyak perkara bukan penentuan yang dimainkan. Data boleh diedarkan dalam tetingkap dan kadangkala mengikut taburan normal. Pada masa lain, ia boleh menjadi tidak menentu tanpa corak yang jelas.
Ini adalah apabila penanda aras mula dimainkan. Melaksanakan kod anda lima kali adalah bagus, tetapi pada penghujung hari, anda hanya mempunyai lima titik data, dengan terlalu banyak nilai diletakkan pada setiap titik data. Kita perlu mempunyai bilangan ulangan yang lebih besar bagi blok kod yang sama untuk melihat corak.
Berapa banyak titik data yang perlu ada? Banyak yang telah ditulis mengenainya, dan salah satu kertas kerja yang saya bincangkan
Penilaian prestasi yang ketat memerlukan penanda aras dibina,
dilaksanakan dan diukur beberapa kali untuk menangani rawak
variasi dalam masa pelaksanaan. Penyelidik harus menyediakan langkah
variasi semasa melaporkan keputusan.
Kalibera, T., & Jones, R. (2013). Penandaarasan yang ketat dalam masa yang munasabah. Prosiding Simposium Antarabangsa 2013 mengenai Pengurusan Memori. https://doi.org/10.1145/2491894.2464160
Apabila mengukur prestasi, kita mungkin ingin mengukur penggunaan CPU, memori atau cakera untuk mendapatkan gambaran yang lebih luas tentang prestasi. Selalunya lebih baik untuk memulakan dengan sesuatu yang mudah, seperti masa berlalu, kerana ia lebih mudah untuk digambarkan. Penggunaan CPU sebanyak 17% tidak memberitahu kami banyak perkara. Apa yang sepatutnya? 20% atau 5? Penggunaan CPU bukanlah salah satu cara semula jadi di mana manusia melihat prestasi.
Saya akan menggunakan kaedah timeit.repeat python untuk mengulang blok pelaksanaan kod mudah. Blok kod hanya mendarab nombor dari 1 hingga 2000.
from functools import reduce reduce((lambda x, y: x * y), range(1, 2000))
Ini ialah tandatangan kaedah
(function) def repeat(
stmt: _Stmt = "pass",
setup: _Stmt = "pass",
timer: _Timer = ...,
repeat: int = 5,
number: int = 1000000,
globals: dict[str, Any] | None = None
) -> list[float]
Apakah ulangan dan nombor?
Mari kita mulakan dengan nombor. Jika blok kod terlalu kecil, ia akan ditamatkan dengan cepat sehingga anda tidak dapat mengukur apa-apa. Argumen ini menyebut bilangan kali stmt perlu dilaksanakan. Anda boleh menganggap ini sebagai blok kod baharu. Apungan yang dikembalikan adalah untuk masa pelaksanaan nombor stmt X.
Dalam kes kami, kami akan mengekalkan nombor sebagai 1000 kerana pendaraban sehingga 2000 adalah mahal.
Seterusnya, teruskan untuk mengulangi. Ini menentukan bilangan ulangan atau bilangan kali blok di atas perlu dilaksanakan. Jika ulangan ialah 5, maka senarai[float] mengembalikan 5 elemen.
Mari kita mulakan dengan mencipta blok pelaksanaan mudah
def run_experiment(number_of_repeats, number_of_runs=1000):
execution_time = timeit.repeat(
"from functools import reduce; reduce((lambda x, y: x * y), range(1, 2000))",
repeat=number_of_repeats,
number=number_of_runs
)
return execution_time
Kami mahu melaksanakannya dalam nilai ulangan yang berbeza
repeat_values = [5, 20, 100, 500, 3000, 10000]
Kod ini agak mudah dan mudah
Kini kami mencapai bahagian paling penting dalam percubaan - iaitu mentafsir data. Harap maklum, bahawa orang yang berbeza boleh mentafsirnya secara berbeza dan tidak ada satu jawapan yang betul.
Takrifan jawapan anda yang betul banyak bergantung pada perkara yang anda cuba capai. Adakah anda bimbang dengan kemerosotan prestasi 95% pengguna anda? Atau, adakah anda bimbang tentang kemerosotan prestasi ekor 5% pengguna anda yang agak lantang?
Seperti yang kita lihat, masa min dan maks adalah buruk. Ia menunjukkan bagaimana satu titik data boleh mencukupi untuk menukar nilai min. Bahagian yang paling teruk ialah min tinggi dan maks tinggi adalah untuk nilai ulangan yang berbeza. Tiada korelasi dan ia hanya mempamerkan kuasa outlier.
Seterusnya kita beralih ke median dan perhatikan bahawa apabila kita meningkatkan bilangan ulangan, median turun, kecuali 20. Apakah yang boleh menjelaskannya? Ia hanya menunjukkan betapa bilangan ulangan yang lebih kecil menunjukkan bahawa kita tidak semestinya mendapat nafas penuh tentang nilai yang mungkin.
Beralih ke min terpenggal, di mana 2.5% terendah dan 2.5% tertinggi dipangkas. Ini berguna apabila anda tidak mengambil berat tentang pengguna luar biasa dan ingin menumpukan pada prestasi 95% pengguna pertengahan anda.
Berhati-hati, cuba meningkatkan prestasi 95% pengguna pertengahan membawa kemungkinan merendahkan prestasi 5% pengguna yang lebih rendah.

Next we want to see where all the data lies. We would use histogram with bin of 10 to see where the data falls. With repetitions of 5 we see that they are mostly equally spaced. This is not one usually expects as sampled data should follow a normal looking distribution.
In our case the value is bounded on the lower side and unbounded on the upper side, since it will take more than 0 seconds to run any code, but there is no upper time limit. This means our distribution should look like a normal distribution with a long right tail.
Going forward with higher values of repeat, we see a tail emerging on the right. I would expect with higher number of repeat, there would be a single histogram bar, which is tall enough that outliers are overshadowed.
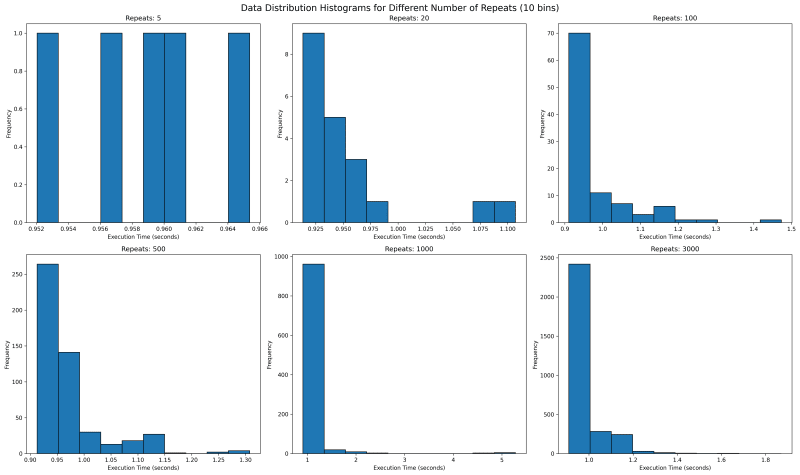
How about we look at larger values of repeat to get a sense? We see something unusual. With 1000 repeats, there are a lot of outliers past 1.8 and it looks a lot more tighter. The one on the right with 3000 repeat only goes upto 1.8 and has most of its data clustered around two peaks.
What can it mean? It can mean a lot of things including the fact that sometimes maybe the data gets cached and at times it does not. It can point to many other side effects of your code, which you might have never thought of. With the kind of distribution of both 1000 and 3000 repeats, I feel the TM95 for 3000 repeat is the most accurate value.

import timeit
import matplotlib.pyplot as plt
import json
import os
import statistics
import numpy as np
def run_experiment(number_of_repeats, number_of_runs=1000):
execution_time = timeit.repeat(
"from functools import reduce; reduce((lambda x, y: x * y), range(1, 2000))",
repeat=number_of_repeats,
number=number_of_runs
)
return execution_time
def save_result(result, repeats):
filename = f'execution_time_results_{repeats}.json'
with open(filename, 'w') as f:
json.dump(result, f)
def load_result(repeats):
filename = f'execution_time_results_{repeats}.json'
if os.path.exists(filename):
with open(filename, 'r') as f:
return json.load(f)
return None
def truncated_mean(data, percentile=95):
data = np.array(data)
lower_bound = np.percentile(data, (100 - percentile) / 2)
upper_bound = np.percentile(data, 100 - (100 - percentile) / 2)
return np.mean(data[(data >= lower_bound) & (data <= upper_bound)])
# List of number_of_repeats to test
repeat_values = [5, 20, 100, 500, 1000, 3000]
# Run experiments and collect results
results = []
for repeats in repeat_values:
result = load_result(repeats)
if result is None:
print(f"Running experiment for {repeats} repeats...")
try:
result = run_experiment(repeats)
save_result(result, repeats)
print(f"Experiment for {repeats} repeats completed and saved.")
except KeyboardInterrupt:
print(f"\nExperiment for {repeats} repeats interrupted.")
continue
else:
print(f"Loaded existing results for {repeats} repeats.")
# Print time taken per repetition
avg_time = statistics.mean(result)
print(f"Average time per repetition for {repeats} repeats: {avg_time:.6f} seconds")
results.append(result)
trunc_means = [truncated_mean(r) for r in results]
medians = [np.median(r) for r in results]
mins = [np.min(r) for r in results]
maxs = [np.max(r) for r in results]
# Create subplots
fig, axs = plt.subplots(2, 2, figsize=(15, 12))
fig.suptitle('Execution Time Analysis for Different Number of Repeats', fontsize=16)
metrics = [
('Truncated Mean (95%)', trunc_means),
('Median', medians),
('Min', mins),
('Max', maxs)
]
for (title, data), ax in zip(metrics, axs.flatten()):
ax.plot(repeat_values, data, marker='o')
ax.set_title(title)
ax.set_xlabel('Number of Repeats')
ax.set_ylabel('Execution Time (seconds)')
ax.set_xscale('log')
ax.grid(True, which="both", ls="-", alpha=0.2)
# Set x-ticks and labels for each data point
ax.set_xticks(repeat_values)
ax.set_xticklabels(repeat_values)
# Rotate x-axis labels for better readability
ax.tick_params(axis='x', rotation=45)
plt.tight_layout()
# Save the plot to a file
plt.savefig('execution_time_analysis.png', dpi=300, bbox_inches='tight')
print("Plot saved as 'execution_time_analysis.png'")
# Create histograms for data distribution with 10 bins
fig, axs = plt.subplots(2, 3, figsize=(20, 12))
fig.suptitle('Data Distribution Histograms for Different Number of Repeats (10 bins)', fontsize=16)
for repeat, result, ax in zip(repeat_values, results, axs.flatten()):
ax.hist(result, bins=10, edgecolor='black')
ax.set_title(f'Repeats: {repeat}')
ax.set_xlabel('Execution Time (seconds)')
ax.set_ylabel('Frequency')
plt.tight_layout()
# Save the histograms to a file
plt.savefig('data_distribution_histograms_10bins.png', dpi=300, bbox_inches='tight')
print("Histograms saved as 'data_distribution_histograms_10bins.png'")
# Create histograms for 1000 and 3000 repeats with 30 bins
fig, axs = plt.subplots(1, 2, figsize=(15, 6))
fig.suptitle('Data Distribution Histograms for 1000 and 3000 Repeats (30 bins)', fontsize=16)
for repeat, result, ax in zip([1000, 3000], results[-2:], axs):
ax.hist(result, bins=100, edgecolor='black')
ax.set_title(f'Repeats: {repeat}')
ax.set_xlabel('Execution Time (seconds)')
ax.set_ylabel('Frequency')
plt.tight_layout()
# Save the detailed histograms to a file
plt.savefig('data_distribution_histograms_detailed.png', dpi=300, bbox_inches='tight')
print("Detailed histograms saved as 'data_distribution_histograms_detailed.png'")
plt.show()
Atas ialah kandungan terperinci timeit.repeat - bermain ulangan untuk memahami corak. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!
 Cara menggunakan fungsi groupby
Cara menggunakan fungsi groupby
 apa itu vuex
apa itu vuex
 Apakah perbezaan antara menyekat dan memadam pada WeChat?
Apakah perbezaan antara menyekat dan memadam pada WeChat?
 Bagaimana untuk membungkus ireport secara automatik
Bagaimana untuk membungkus ireport secara automatik
 pelayan web
pelayan web
 Bagaimana untuk mematikan pusat keselamatan windows
Bagaimana untuk mematikan pusat keselamatan windows
 Fungsi wizard pemacu Windows
Fungsi wizard pemacu Windows
 Bagaimana untuk mewakili nombor negatif dalam binari
Bagaimana untuk mewakili nombor negatif dalam binari




