
Baru-baru ini, Hipotesis Riemann, yang dikenali sebagai salah satu daripada tujuh masalah utama alaf ini, telah mencapai kejayaan baharu.
Hipotesis Riemann ialah masalah yang tidak dapat diselesaikan yang sangat penting dalam matematik, berkaitan dengan sifat tepat taburan nombor perdana (nombor perdana ialah nombor yang hanya boleh dibahagikan dengan 1 dan dirinya sendiri, ia memainkan peranan asas dalam teori nombor Peranan).
Dalam kesusasteraan matematik hari ini, terdapat lebih daripada seribu proposisi matematik berdasarkan penubuhan Hipotesis Riemann (atau bentuk umumnya). Dalam erti kata lain, sebaik sahaja Hipotesis Riemann dan bentuk umumnya dibuktikan, lebih daripada seribu proposisi ini akan ditetapkan sebagai teorem, yang akan memberi kesan yang mendalam terhadap bidang matematik dan jika Hipotesis Riemann terbukti salah, maka antara cadangan ini sebahagian daripadanya juga akan kehilangan keberkesanannya.
Terobosan baharu datang daripada kertas kerja oleh profesor matematik MIT Larry Guth dan profesor Institut Matematik Universiti Oxford dan pemenang Pingat Fields James Maynard. Ahli matematik Terence Tao, yang mengesyorkan kertas itu, berkata mereka menyediakan penambahbaikan besar pertama pada klasik 1940 Ingham terikat pada sifar fungsi zeta Riemannian (dan, lebih umum, untuk mengawal nilai besar pelbagai siri Dirichlet). Sebelum ini, Ingham bound, yang dilahirkan lebih 80 tahun lalu, menyekat ahli matematik daripada melakukan banyak perkara dalam teori nombor analitik kerana kekurangan penambahbaikan.

Walau bagaimanapun, Tao Zhexuan juga berkata walaupun ini merupakan satu kejayaan yang ketara, ia masih jauh daripada menyelesaikan sepenuhnya Hipotesis Riemann, jadi ia harus dilihat secara rasional.
Apakah Hipotesis Riemann?
Hipotesis Riemann atau Hipotesis Riemann telah dicadangkan oleh ahli matematik Jerman Bernhard Riemann pada tahun 1859. Konjektur ini berkait rapat dengan taburan nombor perdana, dan kandungan terasnya melibatkan sifar bukan remeh bagi Fungsi Riemann Zeta.

… mann, Sumber: facts.net/
Kandungan Hipotesis Riemann tidak boleh diterangkan oleh matematik asas sepenuhnya. Secara kasarnya, ia adalah satu tekaan tentang fungsi pembolehubah kompleks yang dipanggil fungsi Riemann zeta (iaitu, fungsi di mana kedua-dua pembolehubah dan nilai fungsi boleh mengambil nilai dalam domain kompleks). Fungsi Riemann zeta, seperti banyak fungsi lain, mempunyai nilai sifar pada titik tertentu dipanggil titik sifar fungsi Riemann zeta. Di antara sifar tersebut, terdapat beberapa sifar bukan remeh penting yang dipanggil fungsi Riemann zeta. Apa yang diramalkan oleh Hipotesis Riemann ialah semua titik sifar bukan remeh diedarkan pada garis lurus khas yang dipanggil "garis kritikal" (dipetik dari blog penulis sains popular Lu Changhai).
Fungsi Riemann ζ ditakrifkan sebagai:
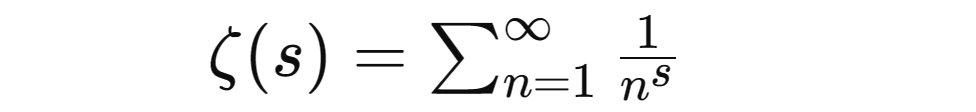
Hipotesis Riemann berpendapat bahawa bahagian sebenar semua sifar bukan remeh bagi fungsi ζ ialah 1/2. Ini bermakna jika ζ(s)=0 dan s ialah sifar bukan remeh (iaitu s bukan genap negatif), maka bahagian sebenar s hendaklah 1/2.
Hipotesis Riemann ialah masalah matematik yang paling penting dan paling dinanti-nantikan di dunia hari ini. Jika sangkaan itu benar, taburan nombor perdana antara nombor asli boleh diterangkan dengan tepat, dan ia akan mempunyai aplikasi dan pengaruh yang luas dalam menyelesaikan teori nombor, analisis kompleks dan cabang matematik yang lain.
Setakat ini, 165 tahun telah berlalu sejak Hipotesis Riemann dicadangkan. Terdapat banyak kajian yang cuba membuktikan Hipotesis Riemann, tetapi semuanya menjadi sia-sia.
Percubaan untuk menyelesaikan Hipotesis Riemann
Sejak Hipotesis Riemann dicadangkan, ramai ahli matematik telah memulakan perjalanan meneroka bukti.
Pada tahun 1896, ahli matematik Perancis Jacques Adamard dan Charles Jean de la Vallée-Poussin secara bebas membuktikan bahawa tiada titik sifar pada garis lurus. Bersama-sama dengan sifat lain yang Riemann telah buktikan untuk sifar bukan remeh, ini menunjukkan bahawa semua sifar bukan remeh mesti terletak pada kawasan. Ini adalah langkah penting dalam bukti lengkap pertama teorem nombor perdana.
Pada tahun 1900, David Hilbert, seorang ahli matematik Jerman dan salah seorang bapa matematik moden, memasukkan Hipotesis Riemann dalam 23 soalannya yang terkenal, dan bersama-sama dengan Hipotesis Goldbach, mereka membentuk senarai Soalan No. 8 Hilbert. Pada masa yang sama, Hipotesis Riemann juga merupakan satu-satunya masalah Hilbert yang dimasukkan ke dalam Hadiah Milenium Institut Matematik Tanah Liat.
Pada tahun 1914, ahli matematik British Godfrey Harold Hardy membuktikan bahawa terdapat titik sifar tak terhingga pada garis lurus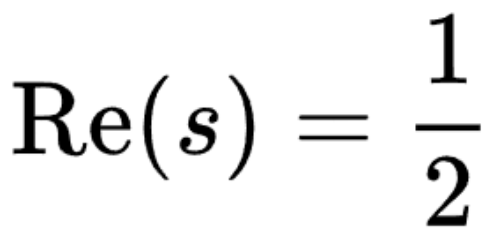 . Kemudian, kerja Hardy dan ahli matematik British John Unther Littlewood pada tahun 1921 dan Selberg pada tahun 1942 (teorem garis kritikal) adalah untuk mengira ketumpatan purata titik sifar pada garis kritikal
. Kemudian, kerja Hardy dan ahli matematik British John Unther Littlewood pada tahun 1921 dan Selberg pada tahun 1942 (teorem garis kritikal) adalah untuk mengira ketumpatan purata titik sifar pada garis kritikal .
.
Sehingga beberapa tahun kebelakangan ini, percubaan untuk membuktikan Hipotesis Riemann sering menimbulkan kekecohan.
Pada September 2018, ucapan yang tidak pernah berlaku sebelum ini di Heidelberg telah meletupkan bulatan matematikBukti Sir Atiyah yang berusia 89 tahun tentang Hipotesis Riemann menarik perhatian global. Di bawah sorotan, Sir Atiyah meluangkan masa selama 45 minit membentangkan kepada dunia bukti tekaan matematik yang mempunyai sejarah lebih 150 tahun ini.
Tetapi bukti Sir Atiyah hanyalah halaman PPT berikut. Bukti sedemikian nampaknya tidak meyakinkan. Apabila ditanya sama ada dia telah menyelesaikan Hipotesis Riemann, dia menjawab, "Ia bergantung pada logik anda. Saya telah membuktikan Hipotesis Riemann yang asal, melainkan anda adalah jenis ahli matematik yang tidak menerima bukti dengan percanggahan tidak menyelesaikan semua masalah, dan akan ada banyak masalah pada masa hadapan Dia hanya mengambil langkah pertama (langkah pertama adalah penyelesaian).
Sedihnya,Tuan Atiyah meninggal dunia pada Januari 2019.

Kini, seseorang telah mencabar Hipotesis Riemann.
Apa yang dilakukan oleh Guth dan Maynard
Berkenaan penemuan baharu Guth dan Maynard, ahli matematik terkenal Teresa Tao mengulas: "Guth dan Maynard telah mencapai kemajuan penting dalam mengkaji Hipotesis Riemann, walaupun mereka masih jauh daripada menyelesaikan perkara yang panjang ini. -masalah tetap. Masalah matematik masih jauh lagi."

Pautan kertas: https://arxiv.org/pdf/2405.20552
Kami belajar daripada tweet Tao Zhexuan bahawa penyelidikan ini adalah kali pertama untuk ahli matematik Albert Ingham Penambahbaikan besar telah dibuat sekitar tahun 1940 dalam batas klasik pada sifar fungsi zeta Riemannian (dan lebih umum pada nilai besar yang mengawal pelbagai siri Dirichlet).
Pada tahun 1940, ahli matematik Albert Ingham mencadangkan satu sempadan yang menerangkan titik sifar ini, yang menjadi asas untuk penyelidikan teori pada masa itu. Walau bagaimanapun, sehingga karya Guth dan Maynard, ikatan ini hampir tidak diperhalusi. Penyelidikan Guth dan Maynard bukan sahaja menambah baik ikatan Ingham ini, tetapi kaedah mereka menyediakan alat dan perspektif baharu untuk menangani nilai besar siri Dirichlet, yang penting dalam banyak teori nombor dan masalah analisis.
Makalah ini membuktikan batasan baru pada kekerapan nilai besar polinomial Dirichlet. Ini memberikan anggaran yang lebih baik untuk polinomial Dirichlet dengan panjang N, dengan nilai yang hampir kepada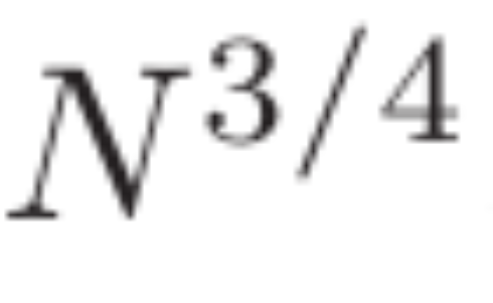 . Tambahan pula, kajian ini memperoleh anggaran ketumpatan titik sifar
. Tambahan pula, kajian ini memperoleh anggaran ketumpatan titik sifar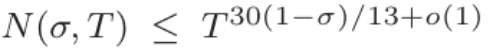 dan ungkapan asimptotik untuk bilangan prima dalam selang panjang panjang
dan ungkapan asimptotik untuk bilangan prima dalam selang panjang panjang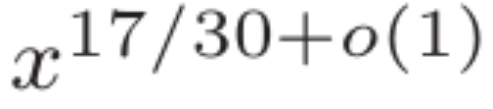 .
.
Tao Zhexuan sendiri memberikan beberapa penjelasan tentang penyelidikan ini dari perspektif matematik. Biarkan ?(σ,?) menandakan bilangan sifar bagi fungsi Riemann ζ di mana bahagian nyata sekurang-kurangnya σ dan bahagian khayalan adalah paling banyak T. Hipotesis Riemann memberitahu kita bahawa N (σ,?) akan hilang untuk sebarang σ>1/2, tetapi hipotesis ini belum dapat dibuktikan lagi. Tetapi sebagai pilihan kedua terbaik, ahli matematik boleh membuktikan anggaran ketumpatan titik sifar, yang merupakan sempadan atas bukan remeh pada ?(σ,?) .
Ternyata σ=3/4 ialah nilai utama. Pada tahun 1940, Ingham memperoleh terikat ?(3/4,?)≪?(3/5+?(1)).
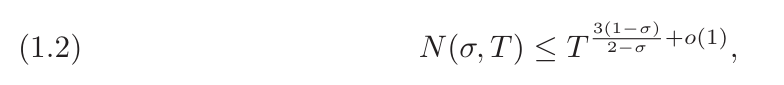
Dalam tempoh lapan puluh tahun akan datang, penambahbaikan pada sempadan ini hanyalah penambahbaikan kecil daripada ralat ?(1). Ini mengehadkan penyelidik untuk menjalankan penyelidikan yang lebih mendalam dalam teori nombor analitik: contohnya, untuk mendapatkan teorem nombor perdana yang baik dalam hampir semua selang pendek bentuk (?,?+?^?), orang telah lama terhad hingga ?>1/6 julat, halangan utama ialah kekurangan penambahbaikan pada sempadan Ingham.

Guth dan Maynard akhirnya menambah baik sempadan Ingham daripada 3/5=0.6 kepada 13/25=0.52. Ini telah menghasilkan banyak penambahbaikan yang sepadan dalam teori nombor analitik Contohnya, penyelidik boleh membuktikan julat teorem nombor perdana dalam hampir mana-mana selang pendek, sekarang dari θ>1/6=0.166… hingga θ>2/15=0.133…

Mengenai pengarang
Larry Guth telah berkhidmat sebagai Claude E. Shannon Profesor Matematik di MIT sejak Julai 2019 dan telah dipilih sebagai Fellow MacVicar pada 2021.
Beliau menerima PhD dari MIT pada tahun 2005 di bawah seliaan Tom Mrowka. Ini diikuti dengan postdoc di Stanford University, jawatan fakulti junior di University of Toronto, dan pada 2011 beliau dilantik sebagai Profesor Institut Courant. Beliau kemudiannya menyertai Jabatan Matematik MIT sebagai profesor pada tahun 2012.
Minat penyelidikan Guth ialah geometri metrik, analisis harmonik dan gabungan nilai ekstrem. Geometri metrik merujuk kepada kajian ketaksamaan yang melibatkan panjang, luas dan isipadu Beberapa contoh utama ialah ketaksamaan isoperimetrik dan ketaksamaan penguncupan. Ketaksamaan pengecutan merupakan tumpuan kerja Guth, dan tumpuan lain ialah mencari hubungan antara ketaksamaan geometri dan topologi.
Baru-baru ini, Guth terlibat dalam penyelidikan mengenai analisis harmonik dan kombinatorik. Banyak kerja berkaitan dengan masalah Kakeya, masalah yang tidak dapat diselesaikan dalam geometri Euclidean, kepada anggaran jenis terhad dalam analisis Fourier, dan kepada anggaran kadar kejadian baris dalam gabungan ekstrem.

seorang ahli matematik British yang bidang penyelidikannya ialah teori nombor analitik, terutamanya teori nombor perdana.
Beberapa masalah yang paling terkenal dalam teori nombor berkaitan dengan pengagihan nombor perdana. Walaupun taburan nombor perdana berskala besar mengikut teorem teori nombor (lebih tepat Hipotesis Riemann), banyak masalah semula jadi perlu menangani skala pendek (atau jarang).James Maynard mencapai keputusan penting pada sangkaan perdana berkembar pada tahun 2013. Dia membuktikan bahawa terdapat pasangan nombor perdana yang tidak terhingga dengan selang kurang daripada 600. Keputusan ini lebih kecil daripada selang 70 juta Zhang Yitang Walaupun kertas kerjanya diterbitkan setengah tahun kemudian daripada Zhang Yitang, keputusannya sangat dipuji di kalangan pakar teori nombor.
Tao Zhexuan mengulas: "Sejujurnya, cara penggambarannya sebenarnya lebih bersih daripada saya... Ternyata kenyataannya lebih kuat sedikit Kaedah Maynard adalah elegan dan berkuasa, dengan cara yang mengejutkan Kaedahnya." menembusi sempadan teori saringan. Dan dalam arah yang kelihatan bertentangan, dia terus menunjukkan bahawa kadangkala bilangan prima jauh lebih jarang daripada purata, masalah Erdő yang terkenal yang tidak membuat sebarang kemajuan yang ketara selama beberapa dekad. Maynard juga melakukan kerja asas dalam bidang penghampiran Diophantine, menyelesaikan tekaan Duffin–Schaeffer dengan Koukoulopoulos, seorang profesor matematik di Universiti Montreal. Konjektur ini, yang dicadangkan pada tahun 1941, boleh dianggap sebagai generalisasi akhir teorem Khintchine, yang menerangkan bagaimana nombor nyata biasa boleh dianggarkan dengan nombor rasional. Pada 2022, Maynard telah dianugerahkan Fields Medal atas sumbangannya kepada teori nombor analitik. Fields Medal adalah anugerah paling berprestij dalam matematik dan sering dianggap sebagai Hadiah Nobel matematik. James Maynard diberi penghormatan atas sumbangannya kepada teori nombor analitik, yang telah membawa kepada kemajuan yang ketara dalam memahami struktur nombor perdana dan penghampiran Diophantine. Pada 2023, dia memenangi satu lagi Anugerah New Horizons dalam Matematik.Nantikan kedua-dua ahli matematik membuat lebih banyak kemajuan dalam masalah dunia seperti Hipotesis Riemann.
Pautan rujukan:
https://www.jiqizhixin.com/articles/2019-01-12
art/557594612
https://news.mit.edu/2014/profile-larry-guth-0527
https://mathstodon.xyz/@tao/112557248794707738
https://zh.wikipedia.org/wiki/% E9% BB%8E% EBC%9% EBC%8% 9C% E6%83% B3
Atas ialah kandungan terperinci Satu kejayaan ketara dalam Hipotesis Riemann! Tao Zhexuan amat mengesyorkan kertas kerja baharu daripada MIT dan Oxford, dan pemenang Fields Medal berusia 37 tahun mengambil bahagian. Untuk maklumat lanjut, sila ikut artikel berkaitan lain di laman web China PHP!




