이 유형의 텍스트를 구문 분석하려면 또 다른 특정 문법 규칙이 필요합니다. 문맥자유문법을 표현할 수 있는 문법 규칙 BNF(Backus Normal Form)와 EBNF(Extended Backus Normal Form)를 소개합니다. 산술 표현식만큼 작은 것부터 거의 모든 프로그래밍 언어만큼 큰 것까지 문맥 자유 문법을 사용하여 정의됩니다.
간단한 산술 표현식의 경우 단어 분할 기술을 사용하여 NUM+NUM*NUM과 같은 입력 토큰 스트림으로 변환했다고 가정합니다(단어 분할 방법에 대해서는 이전 블로그 게시물 참조). . NUM+NUM*NUM(分词方法参见上一篇博文)。
在此基础上,我们定义BNF规则定义如下:
expr ::= expr + term
| expr - term
| term
term ::= term * factor
| term / factor
| factor
factor ::= (expr)
| NUM当然,这种计法还不够简洁明了,我们实际采用的为EBNF形式:
expr ::= term { (+|-) term }*
term ::= factor { (*|/) factor }*
factor ::= (expr)
| NUMBNF和EBNF每一条规则(形如::=的式子)都可以看做是一种替换,即左侧的符号可以被右侧的符号所替换。我们在解析过程中尝试使用BNF/EBNF将输入文本与语法规则进行匹配,以完成各种替换和扩展。在EBNF中,被放置在{...}*内的规则是可选的,而*则表示可以重复零次或多次(类比于正则表达式)。
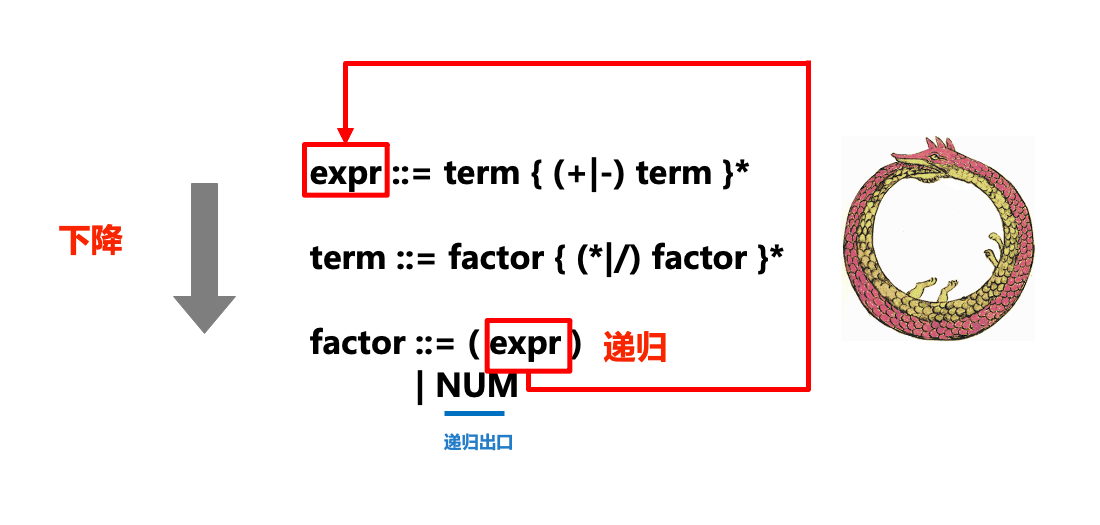
下图形象地展示了递归下降解析器(parser)中“递归”和“下降”部分和ENBF的关系:
在实际的解析过程中,我们对tokens流从左到右进行扫描,在扫描的过程中处理token,如果卡住就产生一个语法错误。每一条语法规则都被转化为一个函数或方法,例如上面的ENBF规则被转换成下述方法:
class ExpressionEvaluator():
...
def expr(self):
...
def term(self):
...
def factor(self):
...在调用某个规则对应方法的过程中,如果我们发现接下来的符号需要采用另一个规则来匹配,则我们就会“下降”到另一个规则方法(如在expr中调用term,term中调用factor),则也就是递归下降中“下降”的部分。
有时也会调用已经在执行的方法(比如在expr中调用term,term中调用factor后,又在factor中调用expr,相当于一条衔尾蛇),这也就是递归下降中“递归”的部分。
对于语法中出现的重复部分(例如expr ::= term { (+|-) term }*),我们则通过while循环来实现。
下面我们来看具体的代码实现。首先是分词部分,我们参照上一篇介绍分词博客的代码。
import re
import collections
# 定义匹配token的模式
NUM = r'(?P<NUM>\d+)' # \d表示匹配数字,+表示任意长度
PLUS = r'(?P<PLUS>\+)' # 注意转义
MINUS = r'(?P<MINUS>-)'
TIMES = r'(?P<TIMES>\*)' # 注意转义
DIVIDE = r'(?P<DIVIDE>/)'
LPAREN = r'(?P<LPAREN>\()' # 注意转义
RPAREN = r'(?P<RPAREN>\))' # 注意转义
WS = r'(?P<WS>\s+)' # 别忘记空格,\s表示空格,+表示任意长度
master_pat = re.compile(
'|'.join([NUM, PLUS, MINUS, TIMES, DIVIDE, LPAREN, RPAREN, WS]))
# Tokenizer
Token = collections.namedtuple('Token', ['type', 'value'])
def generate_tokens(text):
scanner = master_pat.scanner(text)
for m in iter(scanner.match, None):
tok = Token(m.lastgroup, m.group())
if tok.type != 'WS': # 过滤掉空格符
yield tok下面是表达式求值器的具体实现:
class ExpressionEvaluator():
""" 递归下降的Parser实现,每个语法规则都对应一个方法,
使用 ._accept()方法来测试并接受当前处理的token,不匹配不报错,
使用 ._except()方法来测试当前处理的token,并在不匹配的时候抛出语法错误
"""
def parse(self, text):
""" 对外调用的接口 """
self.tokens = generate_tokens(text)
self.tok, self.next_tok = None, None # 已匹配的最后一个token,下一个即将匹配的token
self._next() # 转到下一个token
return self.expr() # 开始递归
def _next(self):
""" 转到下一个token """
self.tok, self.next_tok = self.next_tok, next(self.tokens, None)
def _accept(self, tok_type):
""" 如果下一个token与tok_type匹配,则转到下一个token """
if self.next_tok and self.next_tok.type == tok_type:
self._next()
return True
else:
return False
def _except(self, tok_type):
""" 检查是否匹配,如果不匹配则抛出异常 """
if not self._accept(tok_type):
raise SyntaxError("Excepted"+tok_type)
# 接下来是语法规则,每个语法规则对应一个方法
def expr(self):
""" 对应规则: expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一项
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项,即运算符右值
right = self.term()
if op == "PLUS":
exprval += right
elif op == "MINUS":
exprval -= right
return exprval
def term(self):
""" 对应规则: term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一项
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项,即运算符右值
right = self.factor()
if op == "TIMES":
termval *= right
elif op == "DIVIDE":
termval /= right
return termval
def factor(self):
""" 对应规则: factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 递归出口
return int(self.tok.value)
elif self._accept("LPAREN"):
exprval = self.expr() # 继续递归下去求表达式值
self._except("RPAREN") # 别忘记检查是否有右括号,没有则抛出异常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")我们输入以下表达式进行测试:
e = ExpressionEvaluator()
print(e.parse("2"))
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))求值结果如下:
2
5
14
37
如果我们输入的文本不符合语法规则:
print(e.parse("2 + (3 + * 4)"))则会抛出SyntaxError异常:Expected NUMBER or LPAREN。
综上,可见我们的表达式求值算法运行正确。
上面我们是得到表达式的结果,但是如果我们想分析表达式的结构,生成一棵简单的表达式解析树呢?那么我们需要对上述类的方法做一定修改:
class ExpressionTreeBuilder(ExpressionEvaluator):
def expr(self):
""" 对应规则: expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一项
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项,即运算符右值
right = self.term()
if op == "PLUS":
exprval = ('+', exprval, right)
elif op == "MINUS":
exprval -= ('-', exprval, right)
return exprval
def term(self):
""" 对应规则: term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一项
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一项是"+"或"-"
op = self.tok.type
# 再取下一项,即运算符右值
right = self.factor()
if op == "TIMES":
termval = ('*', termval, right)
elif op == "DIVIDE":
termval = ('/', termval, right)
return termval
def factor(self):
""" 对应规则: factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 递归出口
return int(self.tok.value) # 字符串转整形
elif self._accept("LPAREN"):
exprval = self.expr() # 继续递归下去求表达式值
self._except("RPAREN") # 别忘记检查是否有右括号,没有则抛出异常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")输入下列表达式测试一下:
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))
print(e.parse('2+3+4'))以下是生成结果:
('+', 2, 3)
('+', 2, ('*', 3, 4))
('+', 2, ('*', ('+', 3, 4), 5))
('+', ('+', 2, 3), 4)
可以看到表达式树生成正确。
我们上面的这个例子非常简单,但递归下降的解析器也可以用来实现相当复杂的解析器,例如Python代码就是通过一个递归下降解析器解析的。您要是对此跟感兴趣可以检查Python源码中的Grammar文件来一探究竟。然而,下面我们接着会看到,自己动手写一个解析器会面对各种陷阱和挑战。
任何涉及左递归形式的语法规则,都没法用递归下降parser来解决。所谓左递归,即规则式子右侧最左边的符号是规则头,比如对于以下规则:
items ::= items ',' item
| item完成该解析你可能会定义以下方法:
def items(self):
itemsval = self.items() # 取第一项,然而此处会无穷递归!
if itemsval and self._accept(','):
itemsval.append(self.item())
else:
itemsval = [self.item()]这样做会在第一行就无穷地调用self.items()
expr ::= factor { ('+'|'-'|'*'|'/') factor }*
factor ::= '(' expr ')'
| NUM물론 이 방법은 간결하고 명확하지 않습니다. 우리가 실제로 사용하는 것은 EBNF 형식입니다. rrreee
BNF와 EBNF의 각 규칙( form:: =)은 일종의 대체라고 볼 수 있다. 즉, 왼쪽의 기호를 오른쪽의 기호로 대체할 수 있다. 우리는 다양한 대체와 확장을 완료하기 위해 구문 분석 과정에서 입력 텍스트를 문법 규칙과 일치시키기 위해 BNF/EBNF를 사용하려고 합니다. EBNF에서 {...}* 내에 배치된 규칙은 선택 사항이며, *는 해당 규칙이 0회 이상 반복될 수 있음을 나타냅니다(정규 표현식과 유사). 다음 그림은 재귀 하강 파서(parser)와 ENBF의 "recursion" 부분과 "descent" 부분의 관계를 생생하게 보여줍니다. 🎜🎜 🎜🎜실제 파싱 과정에서는 토큰 스트림을 왼쪽에서 오른쪽으로 스캔하고, 스캔 중에 토큰을 처리합니다. 프로세스가 중단되면 구문 오류가 발생합니다. 각 문법 규칙은 함수나 메서드로 변환됩니다. 예를 들어 위의 ENBF 규칙은 다음 메서드로 변환됩니다. 🎜rrreee🎜특정 규칙에 해당하는 메서드를 호출하는 과정에서 다음 기호가 필요하다고 판단되면 또 다른 규칙을 사용하십시오. 규칙이 일치하면 우리는 재귀 하강의 "내림차순" 부분인 다른 규칙 메소드(예: expr에서 용어 호출 및 용어에서 인수 호출)로 "하강"합니다. 🎜🎜이미 실행 중인 메서드가 호출되는 경우도 있습니다(예: expr에서 항 호출, 항에서 인자 호출, 우로보로스에 해당하는 인자 호출). 이는 재귀 하강 부분의 "재귀" 부분입니다. . 🎜🎜문법에 나타나는 반복되는 부분(예:
🎜🎜실제 파싱 과정에서는 토큰 스트림을 왼쪽에서 오른쪽으로 스캔하고, 스캔 중에 토큰을 처리합니다. 프로세스가 중단되면 구문 오류가 발생합니다. 각 문법 규칙은 함수나 메서드로 변환됩니다. 예를 들어 위의 ENBF 규칙은 다음 메서드로 변환됩니다. 🎜rrreee🎜특정 규칙에 해당하는 메서드를 호출하는 과정에서 다음 기호가 필요하다고 판단되면 또 다른 규칙을 사용하십시오. 규칙이 일치하면 우리는 재귀 하강의 "내림차순" 부분인 다른 규칙 메소드(예: expr에서 용어 호출 및 용어에서 인수 호출)로 "하강"합니다. 🎜🎜이미 실행 중인 메서드가 호출되는 경우도 있습니다(예: expr에서 항 호출, 항에서 인자 호출, 우로보로스에 해당하는 인자 호출). 이는 재귀 하강 부분의 "재귀" 부분입니다. . 🎜🎜문법에 나타나는 반복되는 부분(예: expr ::= 용어 { (+|-) 용어 }*)에 대해서는 while 루프를 통해 구현합니다. 🎜🎜구체적인 코드 구현을 살펴보겠습니다. 첫 번째는 단어분할 부분입니다. 이전 글을 참고하여 단어분할 블로그의 코드를 소개하겠습니다. 🎜rrreee🎜다음은 표현식 평가기의 구체적인 구현입니다. 🎜rrreee🎜테스트를 위해 다음 표현식을 입력합니다. 🎜rrreee🎜평가 결과는 다음과 같습니다. 🎜🎜2🎜입력한 텍스트가 문법 규칙을 준수하지 않는 경우: 🎜rrreee🎜, SyntaxError 예외가 발생합니다:
5
1437🎜
Expected NUMBER or LPAREN. 🎜('+', 2, 3)🎜 표현식 트리가 올바르게 생성된 것을 확인할 수 있습니다. 🎜🎜 위의 예는 매우 간단하지만 재귀 하강 파서를 사용하여 매우 복잡한 파서를 구현할 수도 있습니다. 예를 들어 Python 코드는 재귀 하강 파서를 통해 파싱됩니다. 이에 관심이 있다면 Python 소스 코드의
(' +', 2, ('*', 3, 4))
('+', 2, ('*', ('+', 3, 4), 5))
(' +', ('+', 2, 3), 4)🎜
Grammar 파일을 확인하여 알아볼 수 있습니다. 그러나 아래에서 볼 수 있듯이 파서를 직접 작성하는 데는 다양한 함정과 어려움이 따른다. 🎜self.items()에서 무한히 호출됩니다. 이로 인해 무한 재귀 오류가 발생합니다. 🎜🎜연산자 우선순위 등 문법 규칙 자체에도 오류가 있습니다. 연산자 우선순위를 무시하고 다음과 같이 표현식을 직접 단순화하면: 🎜rrreee🎜PYTHON 전체 화면 복사🎜🎜이 구문은 기술적으로 구현할 수 있지만 계산 순서 규칙을 따르지 않아 계산 결과는 "3+4* 5인치는 예상된 23이 아닌 35입니다. 따라서 계산 결과의 정확성을 보장하려면 별도의 expr 및 term 규칙이 필요합니다. 🎜위 내용은 Python에서 재귀 하강 파서를 구현하는 방법의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!