배열의 역로그를 계산하기 위해 병합 정렬 알고리즘을 사용하여 작성된 C/C++ 프로그램이 있습니까?

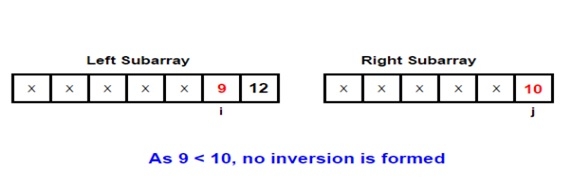
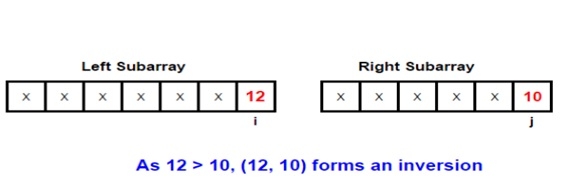
Input: arr[] = { 1, 9, 6, 4, 5} Output: Inversion count is 5

#include  int Merge(int arr[], int aux[], int low, int mid, int high) { int k = low, i = low, j = mid + 1; int inversionCount = 0; while (i <= mid && j <= high) { if (arr[i] <= arr[j]) { aux[k++] = arr[i++]; } else { aux[k++] = arr[j++]; inversionCount += (mid - i + 1); // NOTE } } while (i <= mid) aux[k++] = arr[i++]; for (int i = low; i <= high; i++) arr[i] = aux[i]; return inversionCount; } int MergeSort(int arr[], int aux[], int low, int high) { if (high == low) // if run size == 1 return 0; int mid = (low + ((high - low) >> 1)); int inversionCount = 0; inversionCount += MergeSort(arr, aux, low, mid); inversionCount += MergeSort(arr, aux, mid + 1, high); inversionCount += Merge(arr, aux, low, mid, high); return inversionCount; } int main() { int arr[] = { 1, 9, 6, 4, 5 }; int N = 5; int aux[N]; for (int i = 0; i < N; i++) aux[i] = arr[i]; printf("Inversion count is %d", MergeSort(arr, aux, 0, N - 1)); return 0; }