Python에서 마법 기능과 양자 컴퓨팅 시뮬레이션을 구현하는 방법은 무엇입니까?

양자 컴퓨팅 시뮬레이션 배경

ProjectQ는 매우 우아한 오픈 소스 양자 컴퓨팅 프로그래밍 프레임워크입니다. 원본 작성자는 스위스 연방 공과 대학의 Dr. Damian과 Thomas입니다. 이 양자 컴퓨팅 프로그래밍 프레임워크는 양자 컴퓨팅 애플리케이션 -> 양자 회로 컴파일 -> 해밀턴 시뮬레이션 -> 양자 컴퓨팅 시뮬레이션 -> 양자 하드웨어 API 도킹으로 구현되는 매우 포괄적인 양자 컴퓨팅 프로그래밍 프레임워크입니다. pip를 사용한 설치 지원: python3 -m pip install projectq --upgrade.

projectq를 사용하여 양자 컴퓨팅을 시뮬레이션하는 방법에 대한 예를 살펴보겠습니다.

[dechin@dechin-manjaro simulator]$ ipython
Python 3.8.5 (default, Sep  4 2020, 07:30:14) 
Type 'copyright', 'credits' or 'license' for more information
IPython 7.19.0 -- An enhanced Interactive Python. Type '?' for help.
 
In [1]: from projectq import MainEngine
 
In [2]: from projectq.ops import X
 
In [3]: eng = MainEngine()
 
In [4]: qubits = eng.allocate_qureg(2)
 
In [5]: X | qubits[0]
 
In [6]: from projectq.ops import CX
 
In [7]: CX | (qubits[0], qubits[1])
 
In [8]: eng.flush()
 
In [9]: print (eng.backend.cheat()[1])
[0j, 0j, 0j, (1+0j)]

이 경우 총 2개의 큐비트를 할당했으며 이 2개의 비트의 초기 상태는 모두 |0⟩ projectq의 진폭 벡터 출력은 [1, 0, 0, 0]이어야 합니다. 이 벡터의 네 가지 요소는 각각 네 가지 양자 상태 00, 01, 10 및 11의 확률 진폭에 해당합니다. 측정 중인 특정 상태의 확률을 계산해야 하는 경우 이에 대해 모듈로 제곱 연산을 수행해야 합니다. :

P(00)=(a₀₀+b₀₀i)(a₀₀−b₀₀i)

확률 진폭은 복소수(복소수)라는 점에 유의하세요. 따라서 conjugation 후 내적 연산을 수행해야 합니다.

위의 projectq 사용 사례로 돌아가면, 이 경우에는 두 비트를 할당한 후 첫 번째 비트에 대해 Pauli 행렬 σ^X 연산을 수행한 다음 얽힘 게이트 연산 CX를 수행합니다. 여기서 CX(i,j) 양자 게이트 작업에 해당하는 작업은 다음과 같습니다. 큐비트 i가 |0& 상태이면 아무 작업도 수행되지 않지만, 큐비트 i가 |1⟩ 상태이면 큐비트 j는 다음과 같습니다. 역연산, 즉 원래 j가 |0⟩이면 |1⟩이 되고, 원래 j가 |1⟩이면 |0⟩이 됩니다. 이것이 양자 컴퓨팅에서 양자 얽힘의 역할이며, 실제 하드웨어 시스템에서 다중 비트 게이트 연산을 고품질로 구현하는 것은 여전히 ​​큰 문제입니다. 양자 중첩 특성은 큐비트가 |0⟩ 상태에 있을 수도 있고, |1⟩ 상태에 있을 수도 있고, |0⟩과 |1⟩ 사이의 중간 상태에 있을 수도 있다는 점에서 반영됩니다. 위에서 언급한 바와 같이 |0⟩과 |1⟩을 확률 진폭의 형태로 나누면 다음과 같습니다. b

i)P(1)=(a₁+b₁i)⋅(a₁−b

i)이러한 확률 진폭은 다음과 같이 정리할 수 있습니다. 벡터의 형태 Get up: |ψ⟩=(a₀+b₀i,a

+b

i)_T결국, 이 벡터의 요소는 비트 수에 따라 증가합니다. 비트 수는 기하급수적으로 증가합니다. 비트 수가 41로 증가하면 저장에 필요한 메모리 공간이 32TB 이상 필요합니다! 계산 과정에서 모든 확률 진폭을 메모리에 로드해야 하기 때문에 이는 메모리만 32TB의 크기가 필요한 하드 디스크 저장 공간과는 다릅니다. 따라서 클래식 컴퓨터를 사용하여 양자 컴퓨팅을 시뮬레이션하는 것은 실제로 리소스를 많이 소모하는 방법입니다. 물론 양자컴퓨팅 시뮬레이터는 여전히 연구 가치가 있다. 양자칩의 규모와 품질을 향상시킬 수 없는 현 단계에서는 시뮬레이터가 중요한 역할을 한다. Python의 매직 함수 구현독자가 Python의 매직 함수에 대한 자세하고 포괄적인 구현 계획을 알고 싶다면 이 기사의 참조 링크에서 두 가지 좋은 기사를 얻을 수 있습니다. 여기서는 위의 projectq 코드 사용 사례에서 사용할 수 있는 일부 함수인 __or__ 및 __str__에만 중점을 두고 이를 간단하게 재현할 수 있습니다. Python의 매직 함수를 사용하면 클래스의 덧셈, 뺄셈, 곱셈, 나눗셈 등 클래스에 대한 특수 연산자를 정의할 수 있습니다. 매직 함수가 도입된 후에는 클래스의 요소를 별도로 연산할 필요가 없습니다. 하지만 사용할 수 있습니다. 매직 함수는 작업을 캡슐화합니다. 최종 효과는 코드에서 직접 연산자를 사용하여 다양한 클래스에 대해 작업을 수행할 수 있다는 것입니다. 예를 들어 class1 + class2와 같은 이진 연산자를 사용자 정의할 수 있습니다. 이 장에서는 자세한 내용을 소개하지 않습니다. 아래의 구체적인 사용 예나 링크의 블로그 게시물을 참조하세요.

양자 상태 정의 및 구현

첫 번째 장의 양자 상태 벡터 소개에 따르면 여기서는 간단한 양자 상태 클래스를 구현할 수 있습니다.

# QubitPair.py
import numpy as np
 
class QubitPair:
    def __init__(self):
        self.state = np.array([1, 0, 0, 0], dtype=complex)
 
    def __str__(self):
        return str(self.state)

이 정의는 다음과 같습니다. 양자 상태 클래스는 매우 간단하며 4×1 행렬입니다. 여기서는 주로 클래스의 문자열 표현을 인쇄하는 데 사용되는 __str__(self)의 마법 함수를 정의한다는 점을 추가해야 합니다. 예를 들어 여기서는 양자 상태 벡터를 str 형식으로 직접 변환한 다음 출력합니다. 그런 다음 사용자 정의 QubitPair 클래스를 인쇄하면 현재 클래스에 해당하는 확률 진폭의 문자열 표현이 표시됩니다.

양자 게이트 연산 정의 및 구현

양자 게이트 연산과 관련하여 이를 양자 상태 벡터에 작용하는 행렬로 간주할 수 있습니다. 여기서 먼저 정의된 게이트 연산의 Python 클래스를 표시한 다음 이를 확장할 수 있습니다.

단위 행렬과 Pauli 행렬의 정의

这些是基本的泡利矩阵，这三个两能级体系的泡利矩阵具有非常好的物理性质，如都是酉矩阵且存在特殊的对易关系等：

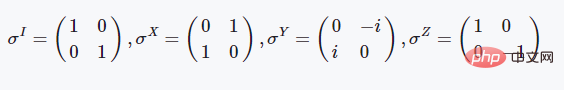
矩阵指数与旋转门操作

矩阵的指数计算一般采用泰勒级数展开的方法来进行定义：

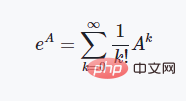
这里如果我们代入上述介绍的泡利矩阵就会得到这样的结果：

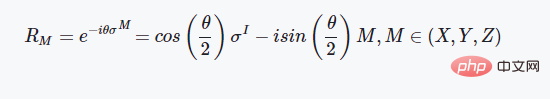
CX门操作的定义

在上述提到的所有的量子门操作中，CX是唯一的一个两比特量子门操作，也就是同时作用在两个量子比特上面，其矩阵形式的定义如下所示：

使用魔法函数__or__来实现量子门操作运算

我们首先简单谈一下为什么要用__or__这个魔法函数而不是其他的二元运算符来实现，这点跟开源库ProjectQ是同步的，理由是我们在量子力学中的运算，一般写成如下的形式：

|ψt⟩=U|ψ0⟩

将量子态写成狄拉克符号的形式，中文称为"左矢"和"右矢"，英文称之为"bra"和"ket"。因此竖线形式的定义，在形式上会更加契合量子力学的思维，当然，就算是换成其他的符号也是无可厚非的。

功能测试验证

在定义了量子态的类和量子门操作的类之后，我们可以写如下所示的一个测试脚本来测试程序的执行效果：

# TestQubits.py
from QubitPair import QubitPair
from Operator import QubitOperator
 
if __name__ == '__main__':
    qubits = QubitPair()
    print ('The initial state is: {}'.format(qubits))
    QubitOperator('X', 3.1415926, 0) | qubits
    print ('Applying X on the 0th qubit...')
    print ('The new state is: {}'.format(qubits))
    QubitOperator('CX') | qubits
    print ('Applying entanglement on qubits...')
    print ('The new state is: {}'.format(qubits))
    QubitOperator('X', 3.1415926, 0) | qubits
    print ('Applying X on the 0th qubit...')
    print ('The new state is: {}'.format(qubits))
    QubitOperator('CX') | qubits
    print ('Applying entanglement on qubits...')
    print ('The new state is: {}'.format(qubits))

这个程序的测试逻辑为：先定义一个两比特的量子系统，然后对第一个比特执行X门操作，使得其从|0〉态变成|1〉态，再对这两个比特执行纠缠门CX操作，观察其态的变化情况。之后再将第一个比特的状态变回|0〉态，再观察作用CX的态的变化情况，执行结果如下所示：

[dechin@dechin-manjaro simulator]$ python3 TestQubits.py 
The initial state is: [1.+0.j 0.+0.j 0.+0.j 0.+0.j]
Applying X on the 0th qubit...
The new state is: [2.67948966e-08+0.j 0.00000000e+00+0.j 0.00000000e+00-1.j
 0.00000000e+00+0.j]
Applying entanglement on qubits...
The new state is: [2.67948966e-08+0.j 0.00000000e+00+0.j 0.00000000e+00+0.j
 0.00000000e+00-1.j]
Applying X on the 0th qubit...
The new state is: [ 7.17966483e-16+0.00000000e+00j -1.00000000e+00+0.00000000e+00j
  0.00000000e+00-2.67948966e-08j  0.00000000e+00-2.67948966e-08j]
Applying entanglement on qubits...
The new state is: [ 7.17966483e-16+0.00000000e+00j -1.00000000e+00+0.00000000e+00j
  0.00000000e+00-2.67948966e-08j  0.00000000e+00-2.67948966e-08j]

这个结果所展示出来的数字也许比较乱，这是因为在运算过程中的计算精度不足所导致的，这里低于1e-06的数字其实我们可以认为就是0。那么我们从这个结果中可以分析总结出量子态的演变历程：

|00〉⇒|10〉⇒|11〉⇒|01〉⇒|01〉

注意：上面的这种写法，其实不太合乎程序语言的逻辑，一般从右到左的方向才是从低位到高位的写法。因此，严格来说写法应该是：|00〉⇒|01〉⇒|11〉⇒|10〉⇒|10〉。

这里我们就完成了基于魔法函数的量子计算模拟的过程，感兴趣的读者可以自行尝试更多的玩法，这里就不进行更多的测试了！

위 내용은 Python에서 마법 기능과 양자 컴퓨팅 시뮬레이션을 구현하는 방법은 무엇입니까?의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!