
확률과 통계에 대한 지식은 데이터 과학과 기계 학습의 핵심입니다. 데이터를 효과적으로 수집, 검토, 분석하려면 통계와 확률에 대한 지식이 필요합니다.
현실 세계에는 본질적으로 통계적이라고 간주되는 현상(예: 날씨 데이터, 판매 데이터, 금융 데이터 등)이 여러 가지 있습니다. 이는 어떤 경우에는 데이터의 특성을 설명할 수 있는 수학적 함수를 통해 자연을 시뮬레이션하는 데 도움이 되는 방법을 개발할 수 있다는 것을 의미합니다. "확률 분포는 실험에서 다양한 결과가 발생할 확률을 제공하는 수학적 함수입니다." 데이터 분포를 이해하면 주변 세계를 더 잘 모델링하는 데 도움이 됩니다. 이는 다양한 결과의 가능성을 결정하거나 사건의 변동성을 추정하는 데 도움이 될 수 있습니다. 이 모든 것이 데이터 과학 및 기계 학습에서 다양한 확률 분포를 이해하는 데 매우 중요합니다. 균일 분포가장 직접적인 분포는 균일 분포입니다. 균일 분포는 모든 결과가 동일하게 나타날 가능성이 있는 확률 분포입니다. 예를 들어 공정한 주사위를 굴렸다면 어떤 숫자가 나올 확률은 1/6입니다. 이는 이산 균일 분포입니다. 그러나 모든 균일 분포가 이산형인 것은 아닙니다. 연속형일 수도 있습니다. 지정된 범위 내에서 실수 값을 사용할 수 있습니다. a와 b 사이의 연속 균일 분포의 확률 밀도 함수(PDF)는 다음과 같습니다. Python에서 이를 인코딩하는 방법을 살펴보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# for continuous
a = 0
b = 50
size = 5000
X_continuous = np.linspace(a, b, size)
continuous_uniform = stats.uniform(loc=a, scale=b)
continuous_uniform_pdf = continuous_uniform.pdf(X_continuous)
# for discrete
X_discrete = np.arange(1, 7)
discrete_uniform = stats.randint(1, 7)
discrete_uniform_pmf = discrete_uniform.pmf(X_discrete)
# plot both tables
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,5))
# discrete plot
ax[0].bar(X_discrete, discrete_uniform_pmf)
ax[0].set_xlabel("X")
ax[0].set_ylabel("Probability")
ax[0].set_title("Discrete Uniform Distribution")
# continuous plot
ax[1].plot(X_continuous, continuous_uniform_pdf)
ax[1].set_xlabel("X")
ax[1].set_ylabel("Probability")
ax[1].set_title("Continuous Uniform Distribution")
plt.show()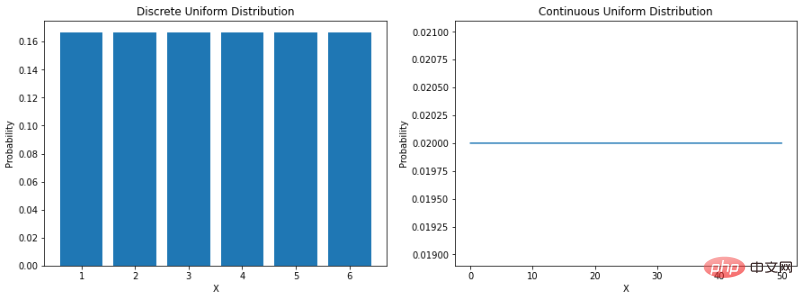
Gaussian distribution
Gaussian 분포는 아마도 가장 일반적으로 듣고 친숙한 분포일 것입니다. 분포. 여기에는 여러 가지 이름이 있습니다. 확률 도표가 종처럼 보이기 때문에 종 곡선이라고 부르는 사람도 있고, 처음 설명한 독일 수학자 칼 가우스가 이름을 붙였기 때문에 가우스 분포라고 부르는 사람도 있고, 초기 통계학자가 발견했기 때문에 정규 분포라고 부르는 사람도 있습니다. 계속해서 일어나고 있습니다. 정규 분포의 확률 밀도 함수는 다음과 같습니다. σ는 표준 편차이고 μ는 분포의 평균입니다. 정규 분포에서는 평균, 최빈값, 중앙값이 모두 동일합니다. 정규 분포 확률 변수를 그릴 때 곡선은 평균을 기준으로 대칭입니다. 즉, 값의 절반은 중앙 왼쪽에 있고 나머지 절반은 중앙 오른쪽에 있습니다. 그리고 곡선 아래의 전체 면적은 1입니다.
mu = 0
variance = 1
sigma = np.sqrt(variance)
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
plt.subplots(figsize=(8, 5))
plt.plot(x, stats.norm.pdf(x, mu, sigma))
plt.title("Normal Distribution")
plt.show()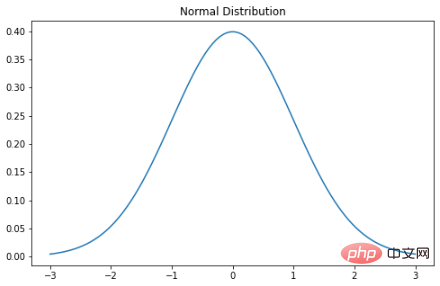
정규분포의 경우. 경험 법칙은 데이터의 몇 퍼센트가 평균에서 특정 표준 편차 수 내에 속하는지 알려줍니다.
로그 정규 분포는 로그 정규 분포를 따르는 확률 변수의 연속 확률 분포입니다. 따라서 확률 변수 X가 로그 정규 분포를 따르는 경우 Y = ln(X)는 정규 분포를 갖습니다. 다음은 로그 정규 분포의 PDF입니다. 로그 정규 분포를 따르는 확률 변수는 양의 실수 값만 취합니다. 따라서 로그 정규 분포는 오른쪽으로 치우친 곡선을 만듭니다. Python으로 플롯해 보겠습니다.
X = np.linspace(0, 6, 500)
std = 1
mean = 0
lognorm_distribution = stats.lognorm([std], loc=mean)
lognorm_distribution_pdf = lognorm_distribution.pdf(X)
fig, ax = plt.subplots(figsize=(8, 5))
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=1")
ax.set_xticks(np.arange(min(X), max(X)))
std = 0.5
mean = 0
lognorm_distribution = stats.lognorm([std], loc=mean)
lognorm_distribution_pdf = lognorm_distribution.pdf(X)
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=0.5")
std = 1.5
mean = 1
lognorm_distribution = stats.lognorm([std], loc=mean)
lognorm_distribution_pdf = lognorm_distribution.pdf(X)
plt.plot(X, lognorm_distribution_pdf, label="μ=1, σ=1.5")
plt.title("Lognormal Distribution")
plt.legend()
plt.show()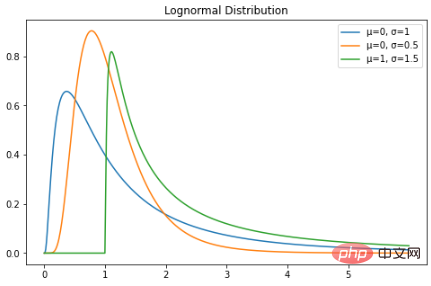
푸아송 분포
푸아송 분포는 프랑스 수학자 Simon Denis Poisson의 이름을 따서 명명되었습니다. 이는 이산 확률 분포입니다. 즉, 결과가 유한한 사건을 계산한다는 의미입니다. 즉, 계산 분포입니다. 따라서 푸아송 분포는 특정 기간 내에 사건이 발생할 수 있는 횟수를 표시하는 데 사용됩니다. 사건이 시간에 따라 고정된 비율로 발생하는 경우 시간에 사건의 수(n)를 관찰할 확률은 포아송 분포로 설명할 수 있습니다. 예를 들어, 고객은 분당 평균 3번의 속도로 커피숍에 도착할 수 있습니다. 푸아송 분포를 사용하여 9명의 고객이 2분 이내에 도착할 확률을 계산할 수 있습니다. 확률 질량 함수 공식은 다음과 같습니다. λ는 시간 단위당 사건 발생률입니다. 이 예에서는 3입니다. k는 발생 횟수입니다. 이 경우에는 9입니다. 여기서 Scipy를 사용하여 확률 계산을 완료할 수 있습니다.
from scipy import stats print(stats.poisson.pmf(k=9, mu=3))
0.002700503931560479
푸아송 분포의 곡선은 정규 분포와 유사하며 λ는 피크 값을 나타냅니다.
X = stats.poisson.rvs(mu=3, size=500)
plt.subplots(figsize=(8, 5))
plt.hist(X, density=True, edgecolor="black")
plt.title("Poisson Distribution")
plt.show()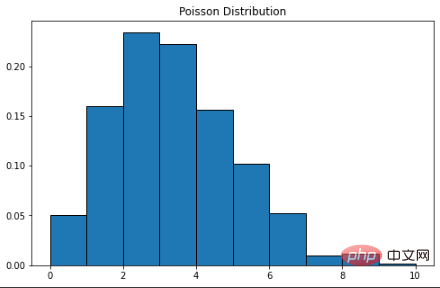
지수 분포
指数分布是泊松点过程中事件之间时间的概率分布。指数分布的概率密度函数如下:λ 是速率参数,x 是随机变量。
X = np.linspace(0, 5, 5000)
exponetial_distribtuion = stats.expon.pdf(X, loc=0, scale=1)
plt.subplots(figsize=(8,5))
plt.plot(X, exponetial_distribtuion)
plt.title("Exponential Distribution")
plt.show()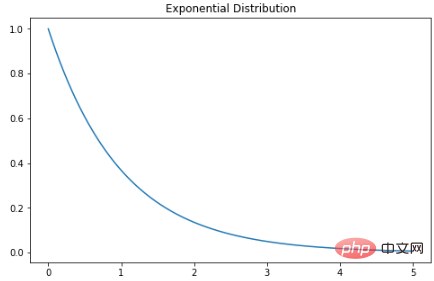
二项分布
可以将二项分布视为实验中成功或失败的概率。有些人也可能将其描述为抛硬币概率。参数为 n 和 p 的二项式分布是在 n 个独立实验序列中成功次数的离散概率分布,每个实验都问一个是 - 否问题,每个实验都有自己的布尔值结果:成功或失败。本质上,二项分布测量两个事件的概率。一个事件发生的概率为 p,另一事件发生的概率为 1-p。这是二项分布的公式:
可视化代码如下:
X = np.random.binomial(n=1, p=0.5, size=1000)
plt.subplots(figsize=(8, 5))
plt.hist(X)
plt.title("Binomial Distribution")
plt.show()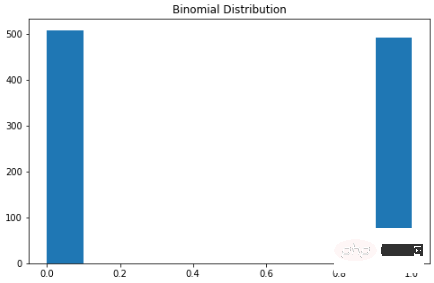
学生 t 分布
学生 t 分布(或简称 t 分布)是在样本量较小且总体标准差未知的情况下估计正态分布总体的均值时出现的连续概率分布族的任何成员。它是由英国统计学家威廉·西利·戈塞特(William Sealy Gosset)以笔名“student”开发的。PDF如下:n 是称为“自由度”的参数,有时可以看到它被称为“d.o.f.” 对于较高的 n 值,t 分布更接近正态分布。
import seaborn as sns
from scipy import stats
X1 = stats.t.rvs(df=1, size=4)
X2 = stats.t.rvs(df=3, size=4)
X3 = stats.t.rvs(df=9, size=4)
plt.subplots(figsize=(8,5))
sns.kdeplot(X1, label = "1 d.o.f")
sns.kdeplot(X2, label = "3 d.o.f")
sns.kdeplot(X3, label = "6 d.o.f")
plt.title("Student's t distribution")
plt.legend()
plt.show()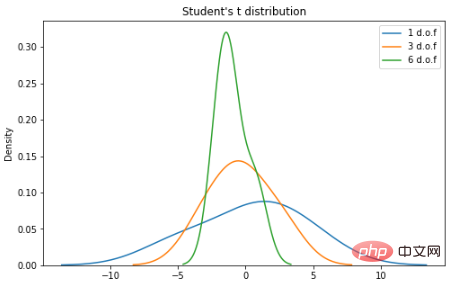
卡方分布
卡方分布是伽马分布的一个特例;对于 k 个自由度,卡方分布是一些独立的标准正态随机变量的 k 的平方和。PDF如下:这是一种流行的概率分布,常用于假设检验和置信区间的构建。在 Python 中绘制一些示例图:
X = np.arange(0, 6, 0.25)
plt.subplots(figsize=(8, 5))
plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f")
plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f")
plt.plot(X, stats.chi2.pdf(X, df=3), label="3 d.o.f")
plt.title("Chi-squared Distribution")
plt.legend()
plt.show()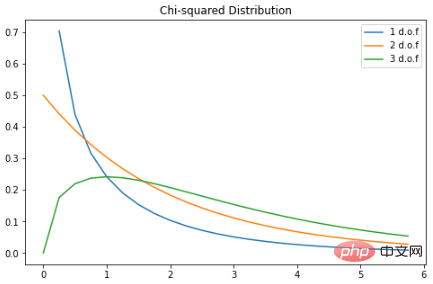
掌握统计学和概率对于数据科学至关重要。在本文展示了一些常见且常用的分布,希望对你有所帮助。
위 내용은 Python은 8가지 확률 분포 공식과 데이터 시각화 튜토리얼을 구현합니다.의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!