PHP 데이터 구조의 그래프 응용 프로그램에서 최단 경로는 무엇입니까?-PHP 튜토리얼-php.cn

그래프 적용: 최단 경로

아직 이전 글에서 최소 스패닝 트리에 대해 더 배울 것이 있다고 생각하시나요? 다들 프림과 크루스칼의 원리를 잘 이해하셨는지 모르겠네요. 면접 때 작성할 수 없다면 대략적인 아이디어라도 주도록 하세요. 물론, 대학원 입시를 치르는 학생이라면 전체 알고리즘의 코드를 깊이 이해하고 기억해야 합니다.

최단 경로는 무엇입니까

오늘 우리는 그래프 응용 프로그램의 또 다른 고전적인 문제인 최단 경로 문제에 대해 배우고 있습니다. 이 문제는 최소 신장 트리의 요구 사항은 모든 노드를 연결하고 가장 작은 가중치를 갖는 경로를 취하는 것입니다. 최단 경로란 한 정점에서 다른 정점까지 가중치가 가장 작은 경로를 말합니다. 이 경로는 최소 스패닝 트리에 반드시 포함되는 것은 아니므로 관련성이 크지 않습니다.

PHP 데이터 구조의 그래프 응용 프로그램에서 최단 경로는 무엇입니까?

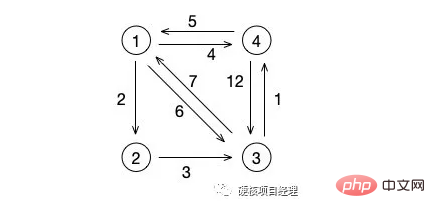
이 그림에서 노드 1에서 노드 2까지의 최단 경로는 2입니다. 이는 명백합니다. 그렇다면 노드 1에서 노드 3까지는 어떨까요? 가중치가 6인 직접 중간 경로가 아니라 전체 가중치가 5인 경로인 1->2->3 경로입니다.

그럼 노드 3을 살펴보겠습니다. 노드 1까지의 최단 경로는 중간 경로가 아니라 가중치가 6인 경로 3->4->1이어야 합니다. 7.

네, 이게 최단 경로 개념이에요. 최단 경로에서는 일반적으로 단방향 그래프의 문제를 해결하지만 실제 생활에서는 어떨까요? 가장 일반적인 지도 관련 애플리케이션은 실제로 양방향 그래프입니다. 그러나 이는 학습에 영향을 미치지 않습니다. 이 예제 다이어그램의 노드는 도시 기차역으로 간주할 수 있습니다. 노드 1과 노드 3을 연결하는 열차 노선도 반드시 동시에 오고 가는 것은 아닙니다. 예를 들어, 창사에서 베이징까지 Z2 열차의 총 운행 시간은 14시간 42분인 반면, Z1 열차의 돌아오는 시간은 14시간 10분입니다. 그러면 다른 기차를 선택할 수 있나요? 예를 들어, 창사에서 스자좡까지 8시간밖에 걸리지 않고, 스자좡에서 베이징까지 2시간밖에 걸리지 않는 기차가 있는데, 이런 식으로 우리가 이 노선을 선택하는 데는 총 10시간밖에 걸리지 않습니다. (물론 이는 단지 예시일 뿐이다. 고속철도가 아니라면 사람들은 반드시 출발역에서 열차를 선택할 것이다.)

다중 소스 최단 경로 플로이드 알고리즘

먼저 다중 소스 최단 경로 알고리즘에 대해 이야기해 보겠습니다. 그렇다면 멀티소스란 무엇인가?

실제로 이 알고리즘은 모든 노드에서 모든 노드까지의 최단 경로를 찾을 수 있습니다. 맞습니다. 이 알고리즘을 사용하면 어느 노드가 어느 노드로 가더라도 그 사이의 최단 경로가 한꺼번에 계산됩니다. 마술적인가요? 아니 아니 아니 더 놀라운 것은, 순간적으로 오! !

function Floyd($graphArr){
    $n = count($graphArr);
    
    for($k = 1;$k<=$n;$k++){ // 设 k 为经过的结点
        for($i = 1;$i<=$n;$i++){
            for($j = 1;$j<=$n;$j++){
                // 如果经过 k 结点 能使 i 到 j 的路径变短，那么将 i 到 j 之间的更新为通过 k 中转之后的结果 
                if($graphArr[$i][$j] > $graphArr[$i][$k] + $graphArr[$k][$j]){
                    $graphArr[$i][$j] = $graphArr[$i][$k] + $graphArr[$k][$j];
                }
            }
        }
    }
    for($i = 1;$i<=$n;$i++){
        for($j = 1;$j<=$n;$j++){
            echo $graphArr[$i][$j], &#39; &#39;;
        }
        echo PHP_EOL;
    }
}
// 请输入结点数：4 
// 请输入边数：8
// 请输入边，格式为 出 入 权：1 2 2
// 请输入边，格式为 出 入 权：1 3 6
// 请输入边，格式为 出 入 权：1 4 4 
// 请输入边，格式为 出 入 权：2 3 3
// 请输入边，格式为 出 入 权：3 1 7
// 请输入边，格式为 出 入 权：3 4 1
// 请输入边，格式为 出 入 权：4 1 5
// 请输入边，格式为 出 入 权：4 3 12
// 0 2 5 4 
// 9 0 3 4 
// 6 8 0 1 
// 5 7 10 0

로그인 후 복사

먼저 결과를 확인할 수 있는데, 댓글 끝에 있는 행렬 출력입니다. 노드 1에서 노드 2, 3, 4까지의 최단 거리는 2, 5, 4입니다. 노드 3에서 노드 1, 2, 4까지의 최단 거리는 6, 8, 1입니다. 즉, 원본 그래프의 인접 행렬이 최단 경로의 행렬이 됩니다. 각 행은 각 노드에서 다른 노드까지의 최단 거리를 나타냅니다.

그래 결과는 괜찮네요. 그럼 정확히 어떤 코드가 쓰여있나요? 이거 뭐야 ㅋ? 걱정하지 마세요. 단계별로 살펴보겠습니다.

두 지점 사이의 거리가 가장 짧지 않다고 가정하면 점프의 매개체가 될 다른 지점이 있어야 합니다. i 지점에서 먼저 이 지점으로 점프한 다음 j 지점으로 점프하는 것이 더 직선적입니다. i가 j에 가까우면 이 지점을 k 지점으로 정의합니다

하지만 어느 노드로 가야 할지 모르고 k가 두 개 이상 있을 수도 있습니다. 어쩌면 i에서 j까지 많은 k를 거쳐야 할 수도 있습니다. 시간이 지나면 루프의 첫 번째 레벨인 k부터 탐색을 시작합니다

루프의 첫 번째 레벨에서 i와 j의 일반적인 탐색 루프를 수행하고 i에서 j까지의 길이, 즉 [i]를 직접 얻습니다. [제이]. 이때, 가장 바깥쪽에 있는 k의 존재로 인해, i가 k에서 걸어가면 k에서 j까지의 길이, 즉 거리 [i][k] + [k][i]도 알 수 있습니다.

물론, 만약 [i][k] + [k][i]의 거리가 [i][j]보다 짧으면 [i][j]의 값이 [i][k] + [k] [i로 업데이트됩니다. ]

내부 i 및 j 루프가 완료된 후 미디어 점프로 첫 번째 노드의 순회도 완료됩니다. 현재 행렬의 각 노드 간 가중치는 첫 번째 노드 이후의 최단 경로를 통해 처리됩니다. media

그러나 이는 정확하지 않을 수 있습니다. i, k1, k2, j를 통과할 수 있는 경로가 가장 짧으므로 외부 k 루프는 계속해서 통과하고 두 번째 노드 포인트는 중간 노드

역할을 합니다. 모든 노드가 중간 중간 노드를 한 번 통과할 때까지 계속되며 최단 경로의 행렬 그래프를 얻습니다. 이것이 위 테스트 코드의 결과 출력입니다.

노드 4와 노드 3에 대해 설명하겠습니다. 4를 i로 정의하고 노드 3을 j로 정의합니다.

初始化时，[i][j] 为 12 ，这个没什么问题，单向图的那条带箭头的边的权值就是 12 。

然后当 k 为 1 时，也就是我们经过结点 1 来看路径有没有变短，这时 [i][k] 是 5 ，[k][j] 是 6 ，OK，路径变成 11 了，把 [i][j] 的值改成 11 。

同时，在 i 为 4 ，j 为 2 的情况下，他们两个的最短路径也在这次 k=1 的循环中被赋值为 7 。最开始 4 到 2 是没有直接的边的，现在在结点 1 的连接下，他们有了路径，也就是 [4][2] = [4][1] + [1][2] = 7 。

当 k 为 2 时，[i][j] 为 11 ，这时 [i][k] 就是上面说过的 [4][2] 。也就是 7 ，而 [k][j] 则是 3 ，路径又缩小了，[i][k] + [k][j] = 10 ，[i][j] 现在又变成了 10 。

循环继续，但已经没有比这条路径更小的值了，所以最后 [4][2] 的最短路径就是 10 。

看着晕吗？拿出笔来在纸上或者本子上自己画画，每一步的 k 都去画一下当前的最短路径矩阵变成什么样了。这样画一次之后，马上就知道这个 Floyd 算法的核心奥秘所在了。

不得不说，前人的智慧真的很伟大吧，不过说是前人，其实 Floyd 大佬在 1962 年才发表了这个算法，但这个算法的核心思想却是数学中的动态规划的思想。所以说，算法和数学是没法分家的，各位大佬哪个不是数学界的一把手呢。

单源最短路径 Dijkstra 算法

说完了多源最短路径，我们再讲一个鼎鼎大名的单源最短路径的算法。虽说上面的多源很牛X，但是它的时间复杂度也就是时间效率也确实是太差了，没看错的话三个 N 次的循环嵌套就是 O(N3)。如果数据稍微多一点的话基本就可以从 Oh!My God! 变成 Oh!FxxK! 了。而且大多数情况下，我们的需求都会是固定的求从某一点到另一点的最短路径问题，也就是单源最短路径问题。这时，就可以使用这种效率稍微好一点的算法来快速地解决了。

// origin 表示源点，也就是我们要看哪个结点到其它结点的最短路径
function Dijkstra($graphArr, $origin)
{
    $n = count($graphArr);
    $dis = []; // 记录最小值
    $book = []; // 记录结点是否访问过
    // 初始化源点到每个点的权值
    for ($i = 1; $i <= $n; $i++) {
        $dis[$i] = $graphArr[$origin][$i]; // 源点到其它点的默认权值
        $book[$i] = 0; // 所有结点都没访问过
    }
    $book[$origin] = 1; // 源点自身标记为已访问
    // 核心算法
    for ($i = 1; $i <= $n - 1; $i++) {
        $min = INFINITY;
        // 找到离目标结点最近的结点
        for ($j = 1; $j <= $n; $j++) {
            // 如果结点没有被访问过，并且当前结点的权值小于 min 值
            if ($book[$j] == 0 && $dis[$j] < $min) {
                $min = $dis[$j]; // min 修改为当前这个节点的路径值
                $u = $j; // 变量 u 变为当前这个结点
            }
            // 遍历完所有结点，u 就是最近的那个顶点
        }
        $book[$u] = 1; // 标记 u 为已访问
        for ($v = 1; $v <= $n; $v++) {
            // 如果 [u][v] 顶点小于无穷
            if ($graphArr[$u][$v] < INFINITY) {
                // 如果当前 dis[v] 中的权值大于 dis[u]+g[u][v]
                if ($dis[$v] > $dis[$u] + $graphArr[$u][$v]) {
                    // 将当前的 dis[v] 赋值为 dis[u]+g[u][v]
                    $dis[$v] = $dis[$u] + $graphArr[$u][$v];
                }
            }
        }
        // 最近的结点完成，继续下一个最近的结点
    }
    for ($i = 1; $i <= $n; $i++) {
        echo $dis[$i], PHP_EOL;
    }
}
// 请输入结点数：4 
// 请输入边数：8
// 请输入边，格式为 出 入 权：1 2 2
// 请输入边，格式为 出 入 权：1 3 6
// 请输入边，格式为 出 入 权：1 4 4 
// 请输入边，格式为 出 入 权：2 3 3
// 请输入边，格式为 出 入 权：3 1 7
// 请输入边，格式为 出 入 权：3 4 1
// 请输入边，格式为 出 入 权：4 1 5
// 请输入边，格式为 出 入 权：4 3 12
// 测试第四个结点到其它结点的最短路径
Dijkstra($graphArr, 4);
// 5
// 7
// 10
// 0

로그인 후 복사

代码一下增加了不少吧，不过仔细看一下核心的算法部分，这次只是两层循环的嵌套了，时间复杂度一下子就降到了 O(N2) ，这一下就比 Floyd 算法提升了很多。当然，它的场景也是有限的，那就是只能一个结点一个结点的计算。

好了，我们还是来看一下 Dijkstra 到底在干嘛吧。我们依然是使用上面那个简单的图，并且还是研究结点 4 到其它结点的算法执行情况。

首先，我们初始化结点 4 到其他所有结点的默认值，这时结点 4 到结点 2 是没有直接路径的，所以是无穷大，而到结点 1 是 5，到结点 3 是 12 。

然后将结点 4 标记为已访问，也就是 book[4] = 1

进入核心算法，从头开始遍历结点，这里是标记为 i 下标，因为这里是单源的最短路径，所以我们不需要再看自己到自己的最短路径了，只需要 n-1 次循环就可以了

开始 j 层的循环，先判断当前的结点是否已经被标记过，没有被标记过的话再看它的值是否是最小的，最后循环完成后获得一个从结点 4 出发的权值最小的路径，并将这条路径到达的结点下标记为 u ，标记 u 下标的这个结点为已访问结点

进入 v 循环，判断图中 u 到 v 的结点是否是无穷，如果不是的话再判断 u 到 v 的结点加上原来的 dis[u] 的权值是否小于 dis[v] 中记录的权值，如果比这个小的话，更新 dis[v] 为 u 到 v 的结点加上原来的 dis[u] 的权值

循环重复地进行比较完成算法

对于结点 4 来说，dis 经历了如下的变化：

首先，默认情况下 dis = [5, 9999999, 12, 0]

第一次循环后，结点1 完成查找，并在 v 的循环中发现了可以从结点1 到结点2 和结点3 而且比原来的值都要小，于是 dis = [5, 7, 11, 0]

第二次循环后，结点2 完成查找，这次循环发现从结点2 到结点3 的距离更短，于是 dis = [5, 7, 10, 0]

第三次循环后，结点3 完成查找，没有发现更短的路径，dis = [5, 7, 10, 0]

看明白了吗？不明白的话自己试试吧，不管是断点还是在中间输出一下 dis 和 book ，都能够帮助我们更好地理解这个算法的每一步是如何执行的。从代码中就可以看出来，这个 Dijkstra 算法的时间复杂度是 O(N2) ，这可比 Floyd 快了不少了吧。

总结

关于图的两种最典型的应用及算法就到这里结束了。当然，图的内容可远不止这些，比较典型的还是进度网络图等的算法，特别是做一些项目管理类的系统时会非常有用。当然，更高深的内容就要去研究《图论》了。这个可就远超我的水平了，希望有更多数学相关基础的同学能够继续深入研究。而我嘛，先去恶补下数学吧！！

测试代码：
https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/5.图/source/5.5图的应用：最短路径.php

로그인 후 복사