C++를 사용하여 최단 경로에 대한 Dijkstra 알고리즘 구현-C#.Net 튜토리얼-php.cn

C++를 사용하여 최단 경로에 대한 Dijkstra 알고리즘 구현

little bottle

풀어 주다： 2019-04-09 10:53:52

앞으로

7645명이 탐색했습니다.

네트워크 계층의 링크 상태 라우팅 알고리즘(LS 알고리즘) 중 하나는 Dijkstra 알고리즘을 사용하여 작성되었습니다. "알고리즘 소개" 소개: Dijkstra의 알고리즘은 가중 방향 그래프의 단일 소스 최단 경로 문제를 해결합니다. 이 알고리즘에서는 모든 간선의 가중치가 음수가 아니어야 합니다.

알고리즘 아이디어

G 집합은 모든 점 집합을 나타내고 S 집합은 소스에서 특정 점까지 최단 경로를 해결한 점 집합을 나타내며 V 집합은 다음을 수행한 점 집합을 나타냅니다. 최단 경로를 해결했습니다
먼저 S=Ø, V=G

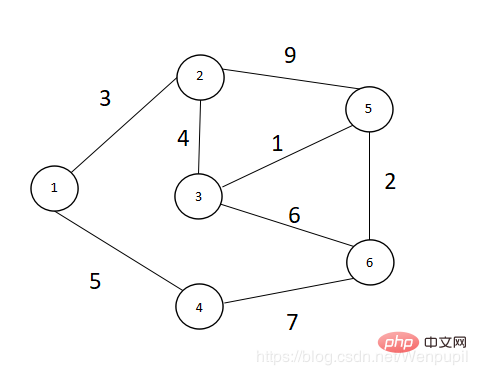
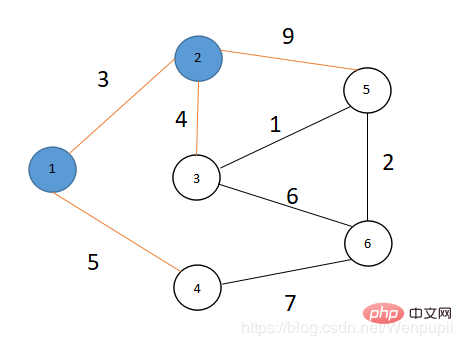
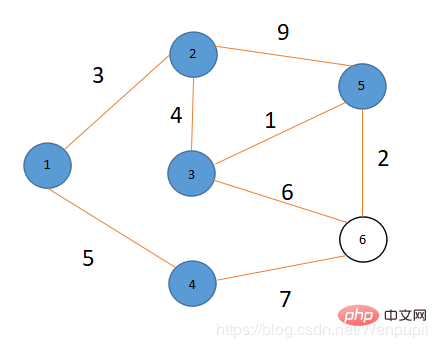
그림과 같이 6개의 점과 8개의 변이 있습니다. V={1,2,3,4,5,6}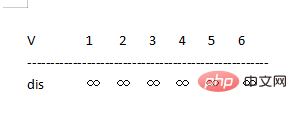
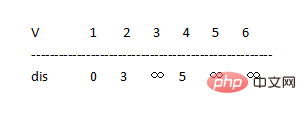
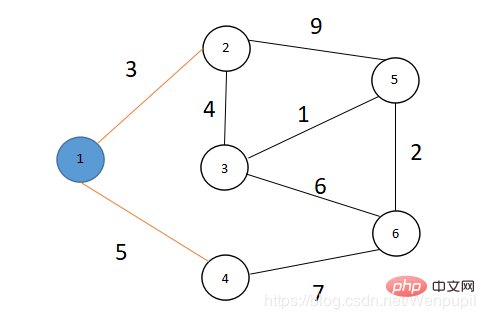
C++를 사용하여 최단 경로에 대한 Dijkstra 알고리즘 구현

u=1을 취하고 점 1을 입력합니다. S, S={1}, V={2,3,4,5,6}을 입력하고, 점 1에 연결된 점을 탐색하고 가중치를 배열에 넣습니다.

4 경로 배열에서 V 집중 지점 2가 이때 가장 짧은 경로를 가지고 있음을 알 수 있으므로(값은 3) u=2, S={1,2}, V라고 합니다. ={3,4,5,6}

왜냐면 dis[3] =dis[2]+4 ⇒ 7=3+4
… dis[5]=dis[2]+9 ⇒ 12=3+9
C++를 사용하여 최단 경로에 대한 Dijkstra 알고리즘 구현

마찬가지로 이제 S={1,2}, V={3,4,5,6}, V에서 dis[3]이 dis[1], dis[를 제외한 최소값임을 알 수 있습니다. 2]이므로 S=S∪{3}
이때 S ={1,2,3},V={4,5,6}

dis[5]=12>dis이기 때문입니다. [3]+1=7+1 ⇒ 하자 dis[5]=dis[3 ]+1=7+1=8
왜냐하면 dis[6]=무한대 >dis[3]+6=7+6 ⇒ 하자 dis[6]=dis[6]+6=7+6=13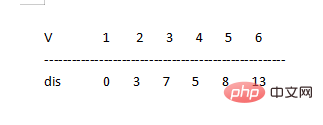
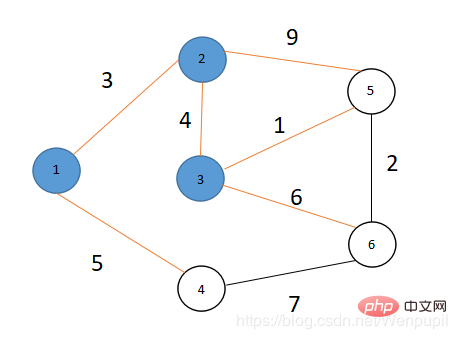
C++를 사용하여 최단 경로에 대한 Dijkstra 알고리즘 구현

마찬가지로 이제 S={1,2,3}, V={4,5,6}, 발견 dis[4 V의 ]는 dis[1], dis[2], dis[3 ]의 덧셈이므로 S=S∪{4}
이때 S={1,2,3,4}, V라고 합시다. ={5,6}

dis[6]=13> dis[4]+7=5+7 ⇒ dis[6]=dis[4]+7=5+7=12
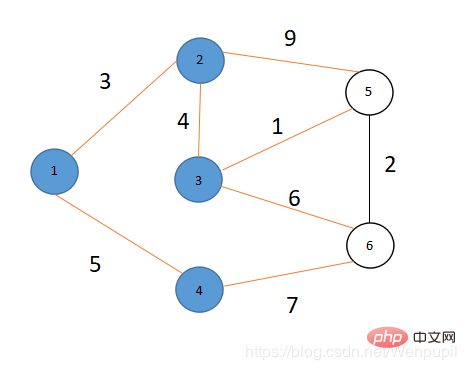
C++를 사용하여 최단 경로에 대한 Dijkstra 알고리즘 구현

마찬가지로, 이제 S={1,2,3,4}, V={5,6}, V에서 dis[5]가 dis[1], dis[2]를 제외한 최소값임을 알 수 있습니다. , dis[3], dis[4]이므로 S=S∪{5 }
이때 S={1,2,3,4,5},V={6}

dis이기 때문에 [6]=12>dis[5]+2=8+2 ⇒ Let dis[ 6]=dis[5]+2=8+2=10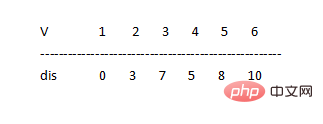
C++를 사용하여 최단 경로에 대한 Dijkstra 알고리즘 구현

지점 1에서 각 지점까지의 최단 경로는 다음과 같습니다. 위와 같이 발견되었습니다. 최근 글이 매우 지저분하고 이해하기 어렵다고 느낍니다. 그런데 이걸 볼 수 있게 해주셔서 모두 감사드립니다.
n개 점과 m개 모서리에 대한 최단 경로를 찾습니다. 일반적으로 모든 점에 대한 최단 경로는 n번 반복하여 얻을 수 있습니다.
이제 코드를 게시할 시간입니다

/*
 * @author Wenpupil
 * @time  2019-04-04
 * @version 1.0
 * @Description 最短路径之Dijkstra算法 关于无负权的无向图练习 
 */
#include<iostream>
#include<cmath>
#include<string.h>
#define INIT  9999
using namespace std;
int map[20][20];              //存储19个点的无向图
int s[20];                    //标记数组 
int dis[20];

void mDijkstra(int i,int m)
{
	for(int i=0;i0){
				dis[j]=min(dis[j],dis[u]+map[u][j]);
			}
		}
	}
}

int main(void)
{
	int m,n;                     //共有m个点，n条边
	cin>>m>>n;
	for(int i=0;i<n int cin>>x>>y>>z;
		map[x][y]=map[y][x]=z;
	}
	mDijkstra(1,m);             //从节点1出发 遍历全图
	
	for(int i=1;i<link href="https://csdnimg.cn/release/phoenix/mdeditor/markdown_views-258a4616f7.css" rel="stylesheet">
<!-- flowchart 箭头图标 勿删 --><svg xmlns="http://www.w3.org/2000/svg" style="display: none;"><path stroke-linecap="round" d="M5,0 0,2.5 5,5z" id="raphael-marker-block" style="-webkit-tap-highlight-color: rgba(0, 0, 0, 0);"></path></svg><h2>
<span style="font-size: 16px;">【추천 과정:</span><a href="//m.sbmmt.com/course/list/38.html" target="_self" style="font-size: 16px; text-decoration: underline;"><span style="font-size: 16px;">C++ 비디오 튜토리얼</span></a><span style="font-size: 16px;">】</span>
</h2></n></string.h></cmath></iostream>

로그인 후 복사

위 내용은 C++를 사용하여 최단 경로에 대한 Dijkstra 알고리즘 구현의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!