부동 소수점 숫자의 표현 범위-JS 튜토리얼-php.cn

부동 소수점 숫자의 표현 범위

清浅

풀어 주다： 2019-03-08 17:00:22

원래의

37710명이 탐색했습니다.

부동 소수점 숫자는 기호, 지수, 가수의 세 부분으로 구성됩니다. 부동 소수점 숫자는 단정밀도 부동 소수점 숫자와 배정밀도 부동 소수점 숫자의 범위는 -3.4E38~3.4입니다. E38, 배정밀도 부동 소수점 숫자의 범위는 -1.79E+308 ~ +1.79E+308

부동 소수점 숫자의 표현 범위

[추천 과정: JavaScript Tutorial]

부동 소수점 숫자 표현

부동 소수점 숫자는 다음과 같이 표현됩니다. 이는 부호, 지수 및 가수의 세 가지 기본 구성 요소로 구성됩니다. 부동 소수점 숫자는 일반적으로 다음 형식으로 표시될 수 있습니다.

여기서 S는 부호 비트, P는 순서 코드, M은 가수입니다.

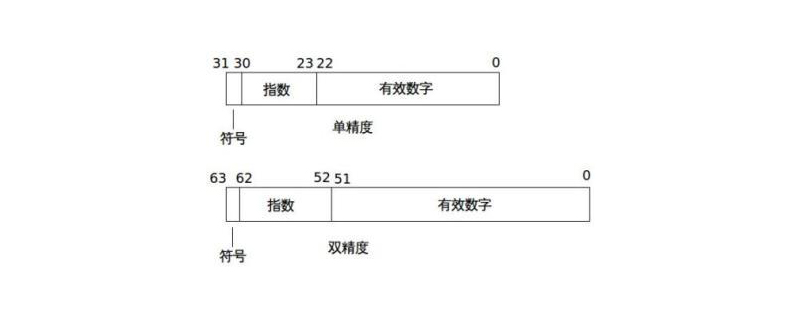
IEEE(Institute of Electrical and Electronics Engineers) 754 표준의 정의에 따르면 단정밀도 부동 소수점 숫자는 32비트(즉, 4바이트)이고 배정밀도 부동 소수점 숫자는 64-비트입니다. 비트(즉, 8바이트)입니다. S, P, M이 차지하는 자릿수와 둘의 표현 방법은 다음 표를 통해 알 수 있다.

단일 정밀도 부동 소수점 수 1(31번째 자리) 23(22~0자리) (-1)^S*2(P-127)*1.M 127 이중 정밀도 부동 소수점 수 1(63번째 비트) 11(62~52비트) 52(51~0비트) (-1)^S*2(P- 1023) *1.M1023

여기서 S는 부호 비트이며 각각 양수와 음수를 나타내는 0과 1입니다.

P는 순서 코드이며 일반적으로 프레임 코드로 표시됩니다. (프레임 코드와 보완 코드는 부호 비트만 반전되어 있고 나머지는 동일합니다. 양수의 경우 원래 코드, 1의 보수 및 1의 보수는 모두 동일합니다. 음수의 경우 보수는 모든 원래 코드의 절대값을 반전한 다음 1)을 추가한 것입니다. 지수 코드는 양수일 수도 있고 음수일 수도 있습니다. 지수 필드에 저장된 값으로 실제 지수 값에 바이어스(Bias) 값을 추가해야 합니다. 단정밀도 숫자의 편차는 127이고 배정도 편차 값은 1023입니다. 예를 들어, 단정밀도의 실제 지수 값 0은 지수 필드에 127로 저장되고 지수 필드에 저장된 64는 실제 지수 값 -63을 나타냅니다. 실제로 지수값을 표현합니다. 범위는 -127~128(양 끝 포함)이 됩니다.

M은 가수로, 단정밀도 숫자는 23비트 길이이고 배정밀도 숫자는 52비트 길이입니다. IEEE 표준에서는 부동 소수점 숫자가 표준이어야 함을 요구합니다. 즉, 가수의 소수점 왼쪽이 1이 되어야 하므로 가수를 저장할 때 소수점 앞의 1을 생략함으로써 바이너리 비트를 확보하여 더 많은 가수를 저장할 수 있다는 뜻이다. 이는 실제로 24비트 가수를 표현하기 위해 23비트 긴 가수 필드를 사용합니다. 예를 들어 단정밀도 숫자의 경우 이진수 1001.101(십진수 9.625에 해당)은 1.001101×23으로 표현할 수 있으므로 가수 필드에 실제로 저장되는 값은 00110100000000000000000, 즉 소수점 왼쪽의 1은 이다. 제거되고 오른쪽에는 0이 사용됩니다.
표준 요구 사항에 따라 정확하게 저장할 수 없는 값은 저장 가능한 가장 가까운 값으로 반올림해야 합니다. 즉, 절반 미만이면 반올림되고, 절반보다 크면(절반 포함), 둥글게 됩니다. 그런데 이진 부동 소수점 숫자의 경우 규칙이 하나 더 있는데, 즉 반올림해야 할 값이 정확히 절반일 때 단순히 반올림하는 것이 아니라 저장 가능한 두 값 중 마지막 값을 등간격으로 반올림하는 것입니다. 이전과 이후의 유효 자릿수는 0입니다.

위 분석에 따르면 IEEE 754 표준에서 정의된 부동 소수점 숫자의 표현 범위는 다음과 같습니다. number

8(30~23자리)

± (2 -2^-23) × 2127~ ± 10^38.53~ ± 10^308.25

이중 정밀도 부동 소수점 수

± (2-2^-52) × 21023

부동소수점 숫자의 표현에는 일정한 범위가 있는데, 그 범위를 벗어나면 오버플로(Flow)가 발생합니다. 일반적으로 가장 큰 절대값보다 큰 데이터를 오버플로(Overflow)라고 하고, 가장 작은 절대값보다 작은 데이터를 말합니다. 값을 언더플로우(Underflow)라고 합니다.

부동 소수점 숫자에 대한 표현 규칙

단정밀도 부동 소수점 숫자와 배정밀도 부동 소수점 숫자는 모두 IEEE 754 표준에 의해 정의됩니다.
　1. P=0, M=0 , 0을 나타냅니다.
　2. P=255이고 M=0이면 무한대를 의미하며, 부호 비트는 양의 무한대인지 음의 무한대인지 판별하는 데 사용됩니다.
　3. P=255이고 M≠0이면 NaN(숫자가 아님, 숫자가 아님)을 의미합니다.
비표준 부동 소수점 수

절댓값이 매우 작은 두 개의 부동 소수점 수를 뺄 때 차이의 지수가 허용 범위를 초과할 수 있으며 결국 대략 0만 될 수 있습니다. 이러한 문제를 해결하기 위해 IEEE 표준에서는 비정규화된 부동 소수점 수를 도입했는데, 이는 부동 소수점 수의 지수가 허용되는 최소 지수 값인 경우 가수를 정규화할 필요가 없다고 규정하고 있습니다. 비표준 부동 소수점 숫자를 사용하면 가수 비트의 암시적 제한이 제거되고 절대값이 더 작은 부동 소수점 숫자를 저장할 수 있습니다. 더욱이, 더 이상 암시적 가수 필드에 의해 제한되지 않기 때문에 위에서 언급한 극히 작은 차이에 대한 문제는 존재하지 않습니다. 왜냐하면 저장할 수 있는 부동 소수점 수 간의 차이도 모두 저장할 수 있기 때문입니다.
IEEE 754 표준의 정의에 따르면 표준 부동 소수점 숫자와 비표준 부동 소수점 숫자의 표현 범위는 다음 표로 요약할 수 있습니다.

	표준 부동 소수점 숫자	비표준 부동 소수점 숫자	소수 근사 범위
단정밀도 부동 소수점 숫자	± 2^-149 ~ (1-2^-23)*2^-126	± 2^-126 ~ (2-2^- 23)*2^127	± ~10 ^-44.85 ~ ~10^38.53
이중 정밀도 부동 소수점 수	± 2^-1074 ~ (1-2^-52)*2^-1022	± 2^-1022 ~ (2-2^ -52)*2^1023	± ~10^-323.3 ~ ~10^308.3

IEEE 754 관련 표준

이 결론 이 기사는 IEEE 754 표준을 기반으로 합니다. 또 다른 표준은 IEEE 854입니다. 이 표준은 소수 부동 소수점 숫자에 관한 것이지만 특정 형식을 지정하지 않으므로 거의 사용되지 않습니다. 또한, 2000년부터 IEEE 754 표준과 IEEE 854 표준을 통합할 목적으로 IEEE 754R이라는 개정이 시작되었습니다. 이 표준의 부동 소수점 형식에 대한 개정 사항은 다음과 같습니다. 1. 16비트 및 128비트 이진 부동 소수점 형식 추가 2. 10진수 부동 소수점 형식 추가 및 IBM에서 제안한 형식 채택.

요약: 위 내용은 이 글의 전체 내용입니다. 모든 분들께 도움이 되었으면 좋겠습니다.

위 내용은 부동 소수점 숫자의 표현 범위의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!