이 글의 내용은 분류 평가 지표와 회귀 평가 지표에 대한 자세한 설명과 Python 코드 구현에 대한 내용입니다. 이제 필요한 친구들이 참고할 수 있도록 공유하겠습니다.
성과 측정(평가) 지표는 크게 두 가지 범주로 나뉜다.
1) 분류 평가 지표(분류), 주로 분석, 이산, 정수. 구체적인 지표로는 정확도(accuracy), 정밀도(precision), 리콜(recall), F값, P-R 곡선, ROC 곡선, AUC 등이 있습니다.
2) 회귀평가지수(regression)는 주로 정수와 실수의 관계를 분석합니다. 구체적인 지표로는 explianed_variance_score, 평균 절대 오차 MAE(mean_absolute_error), 평균 제곱 오차 MSE(mean-squared_error), 평균 제곱근 차이 RMSE, 교차 엔트로피 손실(Log 손실, 교차 엔트로피 손실), R 제곱 값(결정 계수)이 있습니다. , r2_score).
긍정적인 범주와 부정적인 범주만 있다고 가정합니다. 일반적으로 우려되는 범주는 긍정적인 범주이고 다른 범주는 부정적인 범주입니다. 따라서 다중 클래스 문제도 두 가지로 요약될 수 있습니다. 카테고리 )
혼동행렬은 다음과 같습니다
| 실제 카테고리 | 예측 카테고리 | |||
| 긍정적 | 부정적 | summary | ||
| 긍정적 | TP | FN | P(실제로는 긍정) | |
| negative | FP | TN | N(실제로는 부정) | |
AB 모드: 첫 번째는 예측 결과가 right 또는 false , 두 번째 항목은 예측된 카테고리를 나타냅니다. 예를 들어 TP는 참 긍정(True Positive)을 의미합니다. 즉, 올바른 예측은 긍정 클래스입니다. FN은 거짓 부정(False Negative)을 의미합니다. 즉, 잘못된 예측은 부정 클래스입니다.
| 측정 | 정확도(정확도) | 정밀도 ( Precision) | Recall(Recall) | F value |
| Definition | 총 샘플 수 대비 정확하게 분류된 샘플 수의 비율(스팸으로 예측되는 실제 스팸 문자 메시지의 비율) | 결정 as 긍정 사례 수에 대한 참 긍정 사례 수의 비율(올바르게 분류되어 발견된 모든 실제 스팸 문자 메시지의 비율) | 전체 긍정 사례 수에 대한 참 긍정 사례 수의 비율 | 정확도 조화 평균 F-score |
| (재현율 포함)은 | accuracy= | 을 의미합니다.
정밀도= |
회상= |
F- 점수 = |
1. 정밀도는 정밀도율이라고도 하고, 재현율은 재현율이라고도 합니다
2. 더 일반적으로 사용되는 것은 F1,
python3.6 코드 구현:
#调用sklearn库中的指标求解from sklearn import metricsfrom sklearn.metrics import precision_recall_curvefrom sklearn.metrics import average_precision_scorefrom sklearn.metrics import accuracy_score#给出分类结果y_pred = [0, 1, 0, 0] y_true = [0, 1, 1, 1] print("accuracy_score:", accuracy_score(y_true, y_pred)) print("precision_score:", metrics.precision_score(y_true, y_pred)) print("recall_score:", metrics.recall_score(y_true, y_pred)) print("f1_score:", metrics.f1_score(y_true, y_pred)) print("f0.5_score:", metrics.fbeta_score(y_true, y_pred, beta=0.5)) print("f2_score:", metrics.fbeta_score(y_true, y_pred, beta=2.0))
1) P-R curve
단계:
1. "점수" 값을 높은 것에서 낮은 것으로 정렬하고 이를 임계값으로 순서대로 사용합니다.
2. 각 임계값에 대해 이 임계값보다 크거나 같은 "점수" 값을 가진 샘플을 테스트합니다. 긍정적인 사례로 간주되고 나머지는 부정적인 사례로 간주됩니다. 따라서 일련의 예측 수치가 형성됩니다.
eg.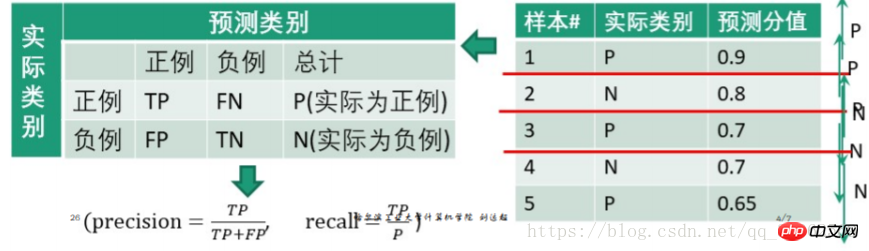
0.9를 임계값으로 설정하면 첫 번째 테스트 샘플은 긍정적인 예이고 2, 3, 4, 5는 부정적인 예입니다.
우리는
#precision和recall的求法如上 #主要介绍一下python画图的库 import matplotlib.pyplot ad plt #主要用于矩阵运算的库 import numpy as np#导入iris数据及训练见前一博文 ... #加入800个噪声特征，增加图像的复杂度 #将150*800的噪声特征矩阵与150*4的鸢尾花数据集列合并 X = np.c_[X, np.random.RandomState(0).randn(n_samples, 200*n_features)] #计算precision，recall得到数组 for i in range(n_classes): #计算三类鸢尾花的评价指标， _作为临时的名称使用 precision[i], recall[i], _ = precision_recall_curve(y_test[:, i], y_score[:,i])#plot作图plt.clf() for i in range(n_classes): plt.plot(recall[i], precision[i]) plt.xlim([0.0, 1.0]) plt.ylim([0.0, 1.05]) plt.xlabel("Recall") plt.ylabel("Precision") plt.show()
| 긍정적인 것으로 예측합니다. 예를 들어 부정적인 예로 예측 된 예는 | toTalSpositive 사례 (점수는 임계 값보다 큽니다) | 0.9 | |
| 1 | 1INGITATION CASE (점수는 임계 값보다 작음) | 0.2+0.3+0.3+0.35 = 1.15 | |
| 4 | 정밀도= | ||
| recall= 임계값 아래 부분은 음의 예로 처리되며 예측된 음의 예의 값은 올바른 예측 값입니다. 즉, 양의 예인 경우 음의 예인 경우 TP가 사용됩니다. TN이 취해지며 둘 다 예측 점수입니다. | Python은 의사 코드를 구현합니다
|||
세로축: True 양성률 tp 비율 = TP / N가로축: 거짓양성률 fp 비율 = FP/N
2) ROC 곡선
단계:
1. "점수" 값을 높은 값에서 낮은 값으로 정렬하여 차례로 임계값으로 사용합니다.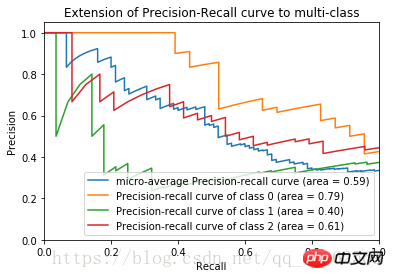
2. 각 임계값에 대해 더 큰 "점수" 값으로 샘플을 테스트합니다. 이 임계값 이상이면 긍정적인 예로 간주되고, 다른 것들은 부정적인 예로 간주됩니다. 따라서 일련의 예측 수치가 형성됩니다.
P-R 곡선 계산과 유사하므로 자세히 설명하지 않겠습니다
붓꽃 데이터 세트의 ROC 이미지는
AUC 값은 분류기에 대한 전체 수치 값을 제공합니다. 일반적으로 AUC가 클수록 분류기가 우수하며 값은 [0, 1]2) 평균 절대 오차 MAE(Mean Absolute Error)
2.2입니다. 회귀 평가 지수
1) 해석 가능한 분산 점수
3) MSE(평균 제곱 오차)
4) 물류 회귀 손실
5) 일관성 평가 - 피어슨 상관 계수 방법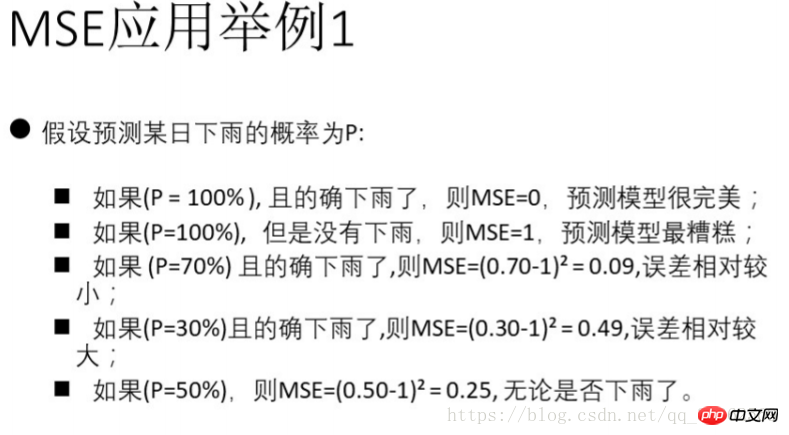
파이썬 코드 구현
from sklearn.metrics import log_loss log_loss(y_true, y_pred)from scipy.stats import pearsonr pearsonr(rater1, rater2)from sklearn.metrics import cohen_kappa_score cohen_kappa_score(rater1, rater2)
위 내용은 분류 평가 지표와 회귀 평가 지표에 대한 자세한 설명과 Python 코드 구현의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!
![[웹 프런트엔드] Node.js 빠른 시작](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
