Modify Graph Edge Weights

2699. Modify Graph Edge Weights

Difficulty:Hard

Topics:Graph, Heap (Priority Queue), Shortest Path

You are given anundirected weighted connectedgraph containing n nodes labeled from 0 to n - 1, and an integer array edges where edges[i] = [a_i, b_i, w_i] indicates that there is an edge between nodes a_iand b_iwith weight w_i.

Some edges have a weight of -1 (w_i= -1), while others have apositiveweight (w_i> 0).

Your task is to modifyall edgeswith a weight of -1 by assigning thempositive integer valuesin the range [1, 2 * 10⁹] so that theshortest distancebetween the nodes source and destination becomes equal to an integer target. If there aremultiple modificationsthat make the shortest distance between source and destination equal to target, any of them will be considered correct.

Returnan array containing all edges (even unmodified ones) in any order if it is possible to make the shortest distance from source to destination equal to target, or anempty arrayif it's impossible.

Note:You are not allowed to modify the weights of edges with initial positive weights.

Example 1:

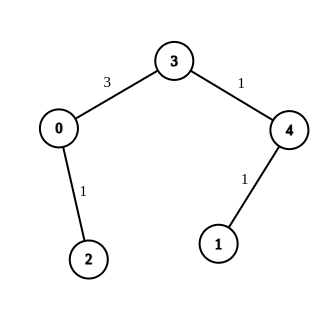
• Input:n = 5, edges = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1]], source = 0, destination = 1, target = 5
• Output:[[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
• Explanation:The graph above shows a possible modification to the edges, making the distance from 0 to 1 equal to 5.

Example 2:

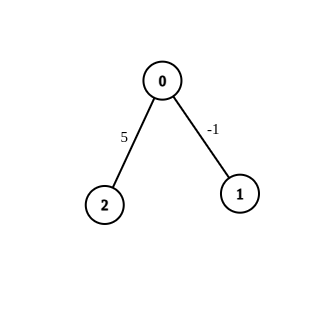
• Input:n = 3, edges = [[0,1,-1],[0,2,5]], source = 0, destination = 2, target = 6
• Output:[]
• Explanation:The graph above contains the initial edges. It is not possible to make the distance from 0 to 2 equal to 6 by modifying the edge with weight -1. So, an empty array is returned.

Example 3:

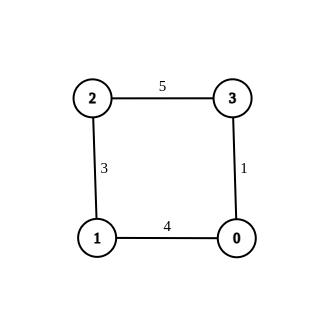
• Input:n = 4, edges = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], source = 0, destination = 2, target = 6
• Output:[[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
• Explanation:The graph above shows a modified graph having the shortest distance from 0 to 2 as 6.

Constraints:

• 1 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= a_i, b_i< n
• w_i= -1 or 1 <= w_i<= 10⁷
• a_i!= b_i
• 0 <= source, destination < n
• source != destination
• 1 <= target <= 10⁹
• The graph is connected, and there are no self-loops or repeated edges

Hint:

1. Firstly, check that it’s actually possible to make the shortest path from source to destination equal to the target.
2. If the shortest path from source to destination without the edges to be modified, is less than the target, then it is not possible.
3. If the shortest path from source to destination including the edges to be modified and assigning them a temporary weight of 1, is greater than the target, then it is also not possible.
4. Suppose we can find a modifiable edge (u, v) such that the length of the shortest path from source to u (dis1) plus the length of the shortest path from v to destination (dis2) is less than target (dis1 + dis2 < target), then we can change its weight to “target - dis1 - dis2”.
5. For all the other edges that still have the weight “-1”, change the weights into sufficient large number (target, target + 1 or 200000000 etc.).

Solution:

We can break down the approach as follows:

Approach:

1. Initial Check with Existing Weights:

   • First, we compute the shortest path from source to destination using only the edges with positive weights, ignoring the edges with weight -1.
   • If this distance is already greater than target, then it's impossible to modify the -1 edges to achieve the target, so we return an empty array.

2. Temporary Assignment of Weight 1:

   • Next, assign a temporary weight of 1 to all edges with weight -1 and recompute the shortest path.
   • If this shortest path is still greater than target, then it's impossible to achieve the target, so we return an empty array.

3. Modify Specific Edge Weights:

   • Iterate through the edges with weight -1 and identify edges that can be adjusted to exactly match the target distance. This is done by adjusting the weight of an edge such that the combined distances of paths leading to and from this edge result in the exact target distance.
   • For any remaining -1 edges, assign a large enough weight (e.g., 2 * 10^9) to ensure they don't impact the shortest path.

4. Return Modified Edges:

   • Finally, return the modified list of edges.

Let's implement this solution in PHP:2699. Modify Graph Edge Weights

        
Explanation:
        

         
The dijkstra function calculates the shortest path from the source to all other nodes.
         
We initially compute the shortest path ignoring -1 edges.
         
If the path without -1 edges is less than the target, the function returns an empty array, indicating it's impossible to adjust the weights to meet the target.
         
Otherwise, we temporarily set all -1 edges to 1 and check if the shortest path exceeds the target.
         
If it does, it's again impossible to reach the target, and we return an empty array.
         
We then modify the weights of -1 edges strategically to achieve the desired shortest path of exactly target.
        
This approach efficiently checks and adjusts edge weights, ensuring that the target distance is met if possible.
Contact Links
If you found this series helpful, please consider giving therepositorya star on GitHub or sharing the post on your favorite social networks ?. Your support would mean a lot to me!
If you want more helpful content like this, feel free to follow me:
        

         
LinkedIn
         
GitHub
        
위 내용은 Modify Graph Edge Weights의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!