이진 검색 트리는 짧은 시간 내에 정렬된 숫자 목록을 유지할 수 있는 데이터 구조입니다. 각 트리 노드에는 두 개의 형제만 있을 수 있으므로 이진 트리라고도 합니다. 이진 검색 트리는 숫자의 존재를 검색하는 데 사용될 수 있습니다. 이를 검색 트리라고 합니다. 실행 시간 복잡도는 O(log(n)) 시간입니다. 이진 탐색 트리와 기본 이진 트리를 구별하는 특징은 다음과 같습니다 –
무료 소프트웨어 개발 과정 시작
웹 개발, 프로그래밍 언어, 소프트웨어 테스팅 등
1. 왼쪽 하위 트리의 노드는 모두 루트 노드보다 작습니다.
2. 오른쪽 하위 트리의 노드는 모두 루트 노드보다 큽니다.
3. 하위 트리의 각 노드는 마찬가지로 BST입니다. 즉, 노드 자체와 동일한 두 가지 특성을 갖습니다.
1. 지정된 배열은 다음과 같습니다.
주어진 배열: [8, 6, 2, 7, 9, 12, 4, 10]
2. 최상위 요소 43부터 시작하겠습니다. 43을 트리의 루트로 삽입하세요.
3. 다음 요소가 루트 노드 요소보다 작을 경우 왼쪽 하위 트리의 루트로 삽입해야 합니다.
4. 그렇지 않은 경우에는 오른쪽 서브트리의 루트로 삽입되어야 합니다.
아래 이미지는 제공된 요소를 이용하여 이진 검색 트리를 구성하는 과정을 보여줍니다.
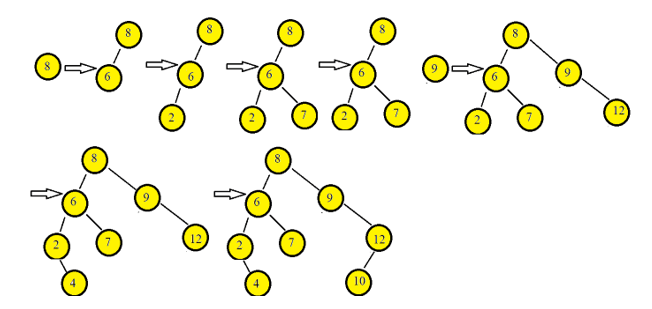
이진 검색 트리 작업:
Java의 이진 검색 트리에서 지원하는 작업은 아래 목록에 나와 있습니다.
1. BST에서 검색 – 이진 검색 트리에서 특정 요소의 위치를 찾습니다.
2. BST에 삽입 – 이진 검색 트리의 적절한 위치에 새 요소를 추가하면 이진 검색 트리 속성이 손상되지 않습니다.
3. BST에서 삭제 – 이진 검색 트리에서 특정 노드를 제거합니다. 그러나 노드의 자식 수에 따라 다양한 삭제 시나리오가 있을 수 있습니다.
이진 검색 트리에서 작업을 수행하기 위한 Java의 이진 검색 트리 예 –
// 프로그램은 Eclipse IDE, JAVA 11에서 테스트할 수 있습니다
package jex;
import java.util.Scanner;
class binarySearchTree {
//node class that defines BST node
class Node {
int key;
Node left, right;
public Node(int data){
key = data;
left = right = null;
}
}
// binary search tree root node
Node root;
// Constructor for binary search tree, first empty tree
binarySearchTree(){
root = null;
}
//delete a node from binary search tree
void deleteKey(int key) {
root = delete(root, key);
}
//recursive delete function
Node delete(Node root, int key) {
// if tree is empty
if (root == null) return root;
//traverse the tree
if (key < root.key)
//traverse left subtree
root.left = delete(root.left, key);
else if (key > root.key)
//traverse right subtree
root.right = delete(root.right, key);
else {
// if node having only one child
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// if node has two children;
root.key = minKey(root.right);
// removing the inorder sibling
root.right = delete(root.right, root.key);
}
return root;
}
int minKey(Node root) {
// initially min is root
int min = root.key;
// find minimum value
while (root.left != null) {
min = root.left.key;
root = root.left;
}
return min;
}
// insert a node in binary search tree
void insertKey(int key) {
root = insert(root, key);
}
// recursively insert a node
Node insert(Node root, int key) {
// initially, tree is empty
if (root == null) {
root = new Node(key);
return root;
}
// traverse the tree
if (key<root.key)
//insert in the left subtree
root.left = insert(root.left, key);
else if (key > root.key)
//insert in the right subtree
root.right = insert(root.right, key);
// return
return root;
}
// function to travel inorder of binary search tree
void inorder() {
inorder(root);
}
// recursively traverse the binary search tree
void inorder(Node root) {
if (root != null) {
inorder(root.left);
System.out.print(root.key + " ");
inorder(root.right);
}
}
boolean searchKey(int key) {
root = search(root, key);
if (root!= null)
return true;
else
return false;
}
//recursive insert function
Node search(Node root, int key) {
// If root is null or key is present at root
if (root==null || root.key==key)
return root;
// when val is greater than root's key
if (root.key > key)
return search(root.left, key);
// when val is lesser than root's key
return search(root.right, key);
}
}
public class client{
public static void main(String[] args) {
binarySearchTree t = new binarySearchTree();
// inserting 8, 6, 2, 7, 9, 12, 4, 10 data into the binary search tree
t.insertKey(8);
t.insertKey(6);
t.insertKey(2);
t.insertKey(7);
t.insertKey(9);
t.insertKey(12);
t.insertKey(4);
t.insertKey(10);
//print the binary search tree
System.out.println( "The binary search tree created with the input data :");
t.inorder();
//delete the leaf node
System.out.println( "\nThe binary search tree after deleting 4 leaf node :");
t.deleteKey(4);
t.inorder();
//delete the node with one child
System.out.println( "\nThe binary search tree after Delete 12 node with 1 child is :");
t.deleteKey(12);
t.inorder();
//search a key in the binary search tree
boolean res = t.searchKey (9);
System.out.println( "\n The node 9 found in binary search tree is :" + res );
res = t.searchKey (12);
System.out.println( "\n The node 10 found in binary search tree is :" + res );
}
}출력:
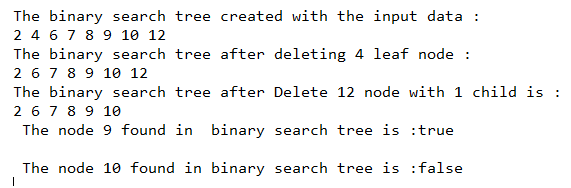
위 프로그램에서와 같이 또 다른 내부 클래스 Node를 포함하고 생성자와 메서드도 포함하는 BinarySearchTree 클래스가 생성됩니다. 클래스에 정의된 메소드는 특정 작업을 수행하기 위한 deleteKey(), delete(), minKey(), insertKey(), insert(), inorder(), searchKey() 및 search()입니다. 기본 함수에서는 BinarySearchTree 클래스 개체가 생성되고 여기에 일부 요소를 삽입한 다음 위 출력에서 볼 수 있듯이 해당 개체에 대해 이진 검색 트리 클래스의 메서드를 호출합니다.
이진 검색 트리는 각 트리 노드가 두 개의 형제만 가질 수 있기 때문에 이진 트리라고도 합니다. 이진 검색 트리는 짧은 시간 내에 정렬된 숫자 목록을 유지할 수 있는 데이터 구조입니다. 이진 검색 트리에서 수행할 수 있는 작업은 순회, 삽입, 삭제, 검색입니다.
위 내용은 Java의 이진 검색 트리의 상세 내용입니다. 자세한 내용은 PHP 중국어 웹사이트의 기타 관련 기사를 참조하세요!