Example analysis of basic commonly used sorting algorithms in JavaScript

This article mainly introduces the basic commonly used sorting algorithms in javascript in detail, which has certain reference value. Interested friends can refer to it

Note: Most of the content is copied from the Internet, and the code is Handwrite it yourself. It is just a review of the past and new knowledge, not originality.

1. Bubble Sort

(1) Algorithm description

Bubble sort is a simple sorting algorithm. It repeatedly walks through the sequence to be sorted, comparing elements two at a time and swapping them if they are in the wrong order. The work of visiting the array is repeated until no more exchanges are needed, which means that the array has been sorted. The name of this algorithm comes from the fact that smaller elements will slowly "float" to the top of the array through swapping.

(2) Algorithm description and implementation

The specific algorithm is described as follows:

<1>. Compare adjacent elements. If the first one is larger than the second one, swap them both; <2>. Do the same for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end, so that the last element It should be the largest number; <3>. Repeat the above steps for all elements, except the last one; <4>. Repeat steps 1~3 until the sorting is completed.

JavaScript code implementation:

Improved bubble sorting: Set an iconic variable pos to record the last exchanged position in each sorting pass . Since the records after the pos position have been swapped in place, only the pos position needs to be scanned during the next sorting pass.

The improved algorithm is as follows:

In traditional bubble sorting, each sorting operation can only find a maximum or minimum value. We consider using The method of performing forward and reverse bubbling in each sorting pass can obtain two final values (the largest and the smallest) at one time, thus reducing the number of sorting passes by almost half.

The improved algorithm is:

The running time of the three algorithms is:

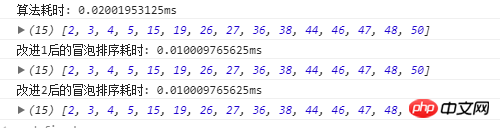
It can be seen from the running results that the time complexity is lower and the time consumption is shorter. You can try it yourself. It is best to write the three algorithms in one file when running, otherwise errors will occur due to browsers and other reasons.

Dynamic diagram demonstration of bubble sorting:

(3) Algorithm analysis

Best case: T(n) = O (n)

When the input data is already in positive sequence

Worst case: T(n) = O(n2)

When the input data is in reverse sequence

Average case: T(n) = O(n2)

2. Selection Sort

The most stable sorting algorithm One, because no matter what data is entered, the time complexity is O(n²)...so when using it, the smaller the data size, the better. The only advantage may be that it does not occupy additional memory space. Theoretically speaking, selection sort may also be the most common sorting method that most people think of when sorting.

(1) Introduction to the algorithm

Selection-sort is a simple and intuitive sorting algorithm. How it works: First, find the smallest (large) element in the unsorted sequence and store it at the starting position of the sorted sequence. Then, continue to find the smallest (large) element from the remaining unsorted elements, and then put it into the sorted sequence. the end of. And so on until all elements are sorted.

(2) Algorithm description and implementation

Direct selection sorting of n records can obtain ordered results through n-1 direct selection sorting. The specific algorithm is described as follows:

<1>. Initial state: the unordered area is R[1..n], the ordered area is empty; <2>. The i-th sorting (i=1 ,2,3…n-1) At the beginning, the current ordered area and unordered area are R[1..i-1] and R(i..n) respectively. This sorting operation selects the record R[k] with the smallest key from the current disordered area, and exchanges it with the first record R in the disordered area, so that R[1..i] and R[i+1 ..n) respectively become a new ordered area with the number of records increased by 1 and a new unordered area with the number of records reduced by 1; <3>.n-1 pass ends, and the array is ordered.

Javascript code implementation:

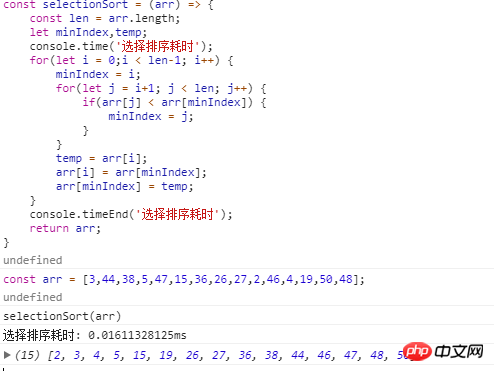
(3) Algorithm analysis

Best case: T (n) = O(n2) Worst case: T(n) = O(n2) Average case: T(n) = O(n2)

The above is the detailed content of Example analysis of basic commonly used sorting algorithms in JavaScript. For more information, please follow other related articles on the PHP Chinese website!