
機械学習における「アンサンブル」という用語は、複数のモデルを並行して組み合わせることを指します。その考え方は、群衆の知恵を利用して、与えられた最終的な答えについてより良い合意を形成することです。

教師あり学習の分野では、この方法は広く研究され、特に RandomForest のような非常に成功したアルゴリズムを使用した分類問題に適用されています。個々のモデルの出力をより堅牢で一貫性のある最終出力に結合するために、投票/重み付けシステムがよく使用されますが、教師なし学習の世界では、このタスクはさらに困難になります。まず、この分野自体の課題が含まれているため、ターゲットと比較するためのデータに関する事前知識がありません。第 2 に、すべてのモデルからの情報を組み合わせる適切な方法を見つけることが依然として問題であり、その方法についてコンセンサスが得られていないためです。
この記事では、このトピックに関する最良のアプローチ、つまり類似性行列のクラスタリングについて説明します。
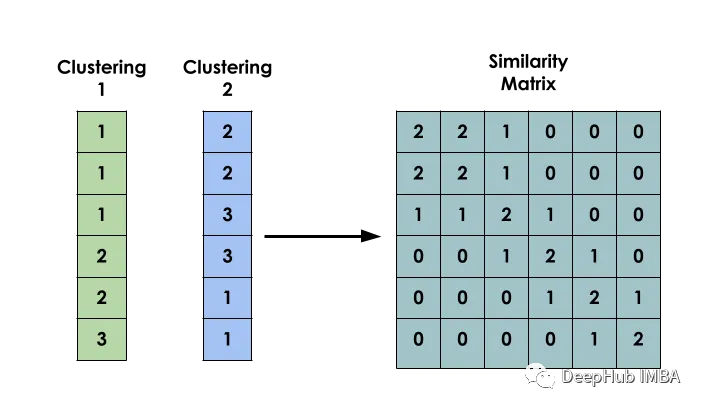 このメソッドの主なアイデアは次のとおりです。データセット X が与えられた場合、Si が xi と xj の類似性を表すような行列 S を作成します。このマトリックスは、いくつかの異なるモデルのクラスタリング結果に基づいて構築されています。
このメソッドの主なアイデアは次のとおりです。データセット X が与えられた場合、Si が xi と xj の類似性を表すような行列 S を作成します。このマトリックスは、いくつかの異なるモデルのクラスタリング結果に基づいて構築されています。
バイナリ共起行列
 it 2 つの入力 i と j が同じクラスターに属しているかどうかを示すために使用されます。
it 2 つの入力 i と j が同じクラスターに属しているかどうかを示すために使用されます。
import numpy as np from scipy import sparse def build_binary_matrix( clabels ): data_len = len(clabels) matrix=np.zeros((data_len,data_len))for i in range(data_len):matrix[i,:] = clabels == clabels[i]return matrix labels = np.array( [1,1,1,2,3,3,2,4] ) build_binary_matrix(labels)
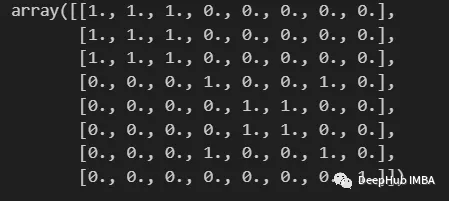 KMeans を使用して類似度行列を構築する
KMeans を使用して類似度行列を構築する
ここでは、M 個の異なるモデルによって生成された M 個の共起行列間の平均値を計算するだけの一般的な方法を紹介します。
 エントリが同じクラスターに属する場合、その類似度の値は 1 に近くなりますが、エントリが異なるグループに属する場合、その類似度の値は 1 に近くなります。は 0 に近くなります
エントリが同じクラスターに属する場合、その類似度の値は 1 に近くなりますが、エントリが異なるグループに属する場合、その類似度の値は 1 に近くなります。は 0 に近くなります
K-Means モデルによって作成されたラベルに基づいて類似度行列を構築します。 MNIST データセットを使用して実施されます。簡素化と効率化のため、PCA で縮小した画像を 10,000 枚のみ使用します。
from sklearn.datasets import fetch_openml from sklearn.decomposition import PCA from sklearn.cluster import MiniBatchKMeans, KMeans from sklearn.model_selection import train_test_split mnist = fetch_openml('mnist_784') X = mnist.data y = mnist.target X, _, y, _ = train_test_split(X,y, train_size=10000, stratify=y, random_state=42 ) pca = PCA(n_components=0.99) X_pca = pca.fit_transform(X)モデル間の多様性を考慮して、各モデルはランダムな数のクラスターでインスタンス化されます。
NUM_MODELS = 500 MIN_N_CLUSTERS = 2 MAX_N_CLUSTERS = 300 np.random.seed(214) model_sizes = np.random.randint(MIN_N_CLUSTERS, MAX_N_CLUSTERS+1, size=NUM_MODELS) clt_models = [KMeans(n_clusters=i, n_init=4, random_state=214) for i in model_sizes] for i, model in enumerate(clt_models):print( f"Fitting - {i+1}/{NUM_MODELS}" )model.fit(X_pca)次の関数は類似度行列を作成するためのものです
def build_similarity_matrix( models_labels ):n_runs, n_data = models_labels.shape[0], models_labels.shape[1] sim_matrix = np.zeros( (n_data, n_data) ) for i in range(n_runs):sim_matrix += build_binary_matrix( models_labels[i,:] ) sim_matrix = sim_matrix/n_runs return sim_matrix
この関数を呼び出します:
models_labels = np.array([ model.labels_ for model in clt_models ]) sim_matrix = build_similarity_matrix(models_labels)
最終結果は次のとおりです:
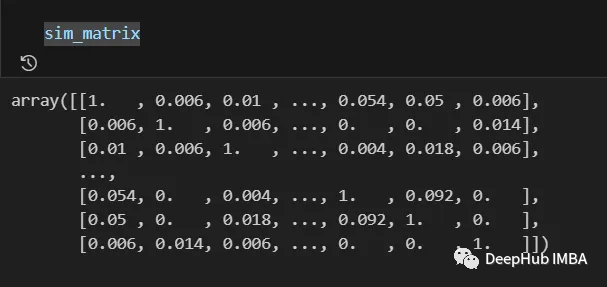 類似度マトリックスからの情報は、対数変換や多項式変換などの適用など、最後のステップの前に後処理することができます。
類似度マトリックスからの情報は、対数変換や多項式変換などの適用など、最後のステップの前に後処理することができます。
今回の場合、元の意図を変更せずに書き直します
Pos_sim_matrix = sim_matrix
類似度行列のクラスタリング
これを使用すると、どのエントリが同じクラスタに属する可能性が高く、どのエントリが属さないかを視覚的に確認できます。ただし、この情報は、類似度行列をパラメータとして受け取ることができるクラスタリング アルゴリズムを使用して、実際のクラスターに変換する必要があります。ここでは SpectralClustering を使用します。
from sklearn.cluster import SpectralClustering spec_clt = SpectralClustering(n_clusters=10, affinity='precomputed',n_init=5, random_state=214) final_labels = spec_clt.fit_predict(pos_sim_matrix)
標準的な KMeans モデルとの比較
KMeans と比較して、私たちの手法が有効であるかどうかを確認してみましょう。
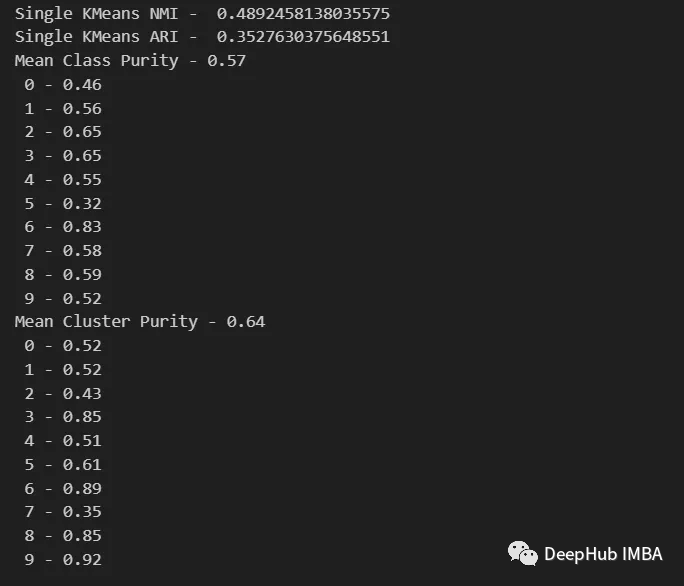
from seaborn import heatmap import matplotlib.pyplot as plt def data_contingency_matrix(true_labels, pred_labels): fig, (ax) = plt.subplots(1, 1, figsize=(8,8)) n_clusters = len(np.unique(pred_labels))n_classes = len(np.unique(true_labels))label_names = np.unique(true_labels)label_names.sort() contingency_matrix = np.zeros( (n_classes, n_clusters) ) for i, true_label in enumerate(label_names):for j in range(n_clusters):contingency_matrix[i, j] = np.sum(np.logical_and(pred_labels==j, true_labels==true_label)) heatmap(contingency_matrix.astype(int), ax=ax,annot=True, annot_kws={"fontsize":14}, fmt='d') ax.set_xlabel("Clusters", fontsize=18)ax.set_xticks( [i+0.5 for i in range(n_clusters)] )ax.set_xticklabels([i for i in range(n_clusters)], fontsize=14) ax.set_ylabel("Original classes", fontsize=18)ax.set_yticks( [i+0.5 for i in range(n_classes)] )ax.set_yticklabels(label_names, fontsize=14, va="center") ax.set_title("Contingency Matrix\n", ha='center', fontsize=20)from sklearn.metrics import normalized_mutual_info_score, adjusted_rand_score def purity( true_labels, pred_labels ): n_clusters = len(np.unique(pred_labels))n_classes = len(np.unique(true_labels))label_names = np.unique(true_labels) purity_vector = np.zeros( (n_classes) )contingency_matrix = np.zeros( (n_classes, n_clusters) ) for i, true_label in enumerate(label_names):for j in range(n_clusters):contingency_matrix[i, j] = np.sum(np.logical_and(pred_labels==j, true_labels==true_label)) purity_vector = np.max(contingency_matrix, axis=1)/np.sum(contingency_matrix, axis=1) print( f"Mean Class Purity - {np.mean(purity_vector):.2f}" ) for i, true_label in enumerate(label_names):print( f" {true_label} - {purity_vector[i]:.2f}" ) cluster_purity_vector = np.zeros( (n_clusters) )cluster_purity_vector = np.max(contingency_matrix, axis=0)/np.sum(contingency_matrix, axis=0) print( f"Mean Cluster Purity - {np.mean(cluster_purity_vector):.2f}" ) for i in range(n_clusters):print( f" {i} - {cluster_purity_vector[i]:.2f}" ) kmeans_model = KMeans(10, n_init=50, random_state=214) km_labels = kmeans_model.fit_predict(X_pca) data_contingency_matrix(y, km_labels) print( "Single KMeans NMI - ", normalized_mutual_info_score(y, km_labels) ) print( "Single KMeans ARI - ", adjusted_rand_score(y, km_labels) ) purity(y, km_labels)data_contingency_matrix(y, final_labels) print( "Ensamble NMI - ", normalized_mutual_info_score(y, final_labels) ) print( "Ensamble ARI - ", adjusted_rand_score(y, final_labels) ) purity(y, final_labels)
#
上記の値を観察すると、Ensemble 法がクラスタリングの品質を効果的に向上させることができることが明確にわかります。同時に、より一貫性のある動作も分割行列で観察され、より適切な分布カテゴリとより少ない「ノイズ」が得られます。
以上が教師なし学習のためのアンサンブル手法: 類似行列のクラスタリングの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。