Java データ構造の収集フレームワークと一般的なアルゴリズムは何ですか?

1 コレクション フレームワーク

1.1 コレクション フレームワークの概念

Java コレクション フレームワーク Java コレクション フレームワークは、コンテナ コンテナとも呼ばれ、定義です。 java.util パッケージ内の一連のインターフェイスとその実装クラス。

その主なパフォーマンスは、複数の要素を 1 つのユニットに配置することです。これは、一般に CRUD として知られる、これらの要素を迅速かつ便利に保存、取得、管理するために使用されます。

クラスとインターフェースの概要:

1.2 コンテナーに関係するデータ構造

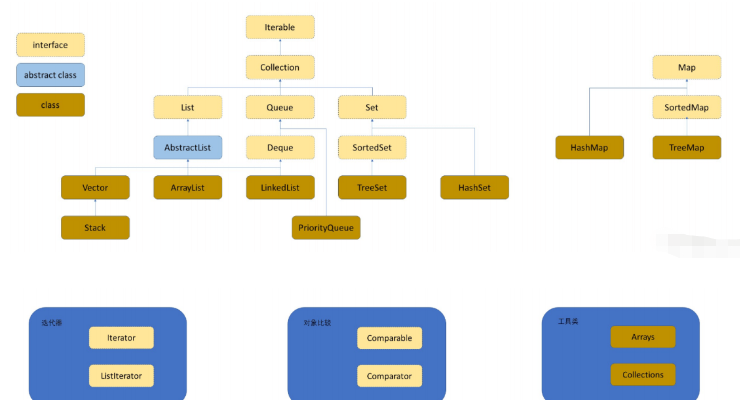
Collection: 最も一般的に使用されるコンテナーを含むインターフェースです。一部のメソッド

List: ArrayList と LinkedList に実装されるメソッドを標準化するインターフェイスです。

• ArrayList: List インターフェイスを実装し、最下層は動的タイプ シーケンス リスト

• LinkedList: List インターフェイスを実装します。最下層は二重リンク リストです

Stack: 最下層はスタックです、スタックは特別なシーケンス リストです

Queue: 最下層はキューであり、特別なシーケンス テーブルです。

Deque: これはインターフェイスです。

Set: Set はインターフェイスであり、K モデルはその中に配置されます

• HashSet: 最下層はハッシュ バケットで、クエリ時間の複雑さは O(1)

• TreeSet: 最下層は赤黒ツリーです。クエリの時間計算量は O()、キー順の

マップ: K-V モデルのキーと値のペアを保存するマッピング

• #HashMap: 最下層はハッシュ バケットで、クエリ時間の複雑さは O(1)

• ツリーマップ: 最下層は赤黒のツリーで、クエリ時間の計算量は O()、キーの順序について

// 请计算一下func1基本操作执行了多少次？
void func1(int N){
	int count = 0;
	for (int i = 0; i < N ; i++) {
		for (int j = 0; j < N ; j++) {
			count++;
		}
	}
	for (int k = 0; k < 2 * N ; k++) {
		count++;
	} 
	int M = 10;
	while ((M--) > 0) {
		count++;
	} 
	System.out.println(count);
}

ログイン後にコピー

• #N = 10 F(N) = 130

• N = 100 F(N) = 10210

• N = 1000 F(N) = 1002010

• 使用 定数 1 は、実行時にすべての加算定数を置き換えます。

• 修正された実行数関数では、最上位の項のみが保持されます。

• 最上位の項が存在し、1 でない場合は、この項に乗じた定数を削除します。結果はビッグオーオーダー。

• N = 10 F (N) = 100

• N = 100 F(N) = 10000

• N = 1000 F(N) = 1000000

が N 回見つかった

平均情况：N/2次找到

在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)

4 空间复杂度

对于一个算法而言，空间复杂度表示它在执行期间所需的临时存储空间大小。空间复杂度的计算方式并非程序所占用的字节数量，因为这并没有太大的意义；实际上，空间复杂度的计算基于变量的数量。大O渐进表示法通常用来计算空间复杂度，其计算规则类似于实践复杂度的计算规则。

实例1:

// 计算bubbleSort的空间复杂度？
void bubbleSort(int[] array) {
	for (int end = array.length; end > 0; end--) {
		boolean sorted = true;
		for (int i = 1; i < end; i++) {
			if (array[i - 1] > array[i]) {
				Swap(array, i - 1, i);
				sorted = false;
			}
		} 
		if(sorted == true) {
		break;
		}
	}
}

实例2:

// 计算fibonacci的空间复杂度？
int[] fibonacci(int n) {
	long[] fibArray = new long[n + 1];
	fibArray[0] = 0;
	fibArray[1] = 1;
	for (int i = 2; i <= n ; i++) {
		fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
	} 
	return fibArray;
}

实例3:

// 计算阶乘递归Factorial的空间复杂度？
long factorial(int N) {
	return N < 2 ? N : factorial(N-1)*N;
}

• 实例1使用了常数个额外空间，所以空间复杂度为 O(1)

• 实例2动态开辟了N个空间，空间复杂度为 O(N)

• 实例3递归调用了N次，开辟了N个栈帧，每个栈帧使用了常数个空间。空间复杂度为O(N)

以上がJava データ構造の収集フレームワークと一般的なアルゴリズムは何ですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。