今年の AI 分野で最も影響力のある開発について語るなら、爆発的な AI マッピングは間違いなくその 1 つです。デザイナーは画像のテキスト説明を入力するだけで、AI が非常に品質の高い高解像度画像を生成します。現在、最も広く使用されているモデルは、StabilityAI のオープンソース モデルである Stable Diffusion であり、このモデルがオープンソース化されると、コミュニティで広範な議論を引き起こしました。
しかし、拡散モデルを使用する際の最大の問題は、サンプリング速度が非常に遅いことです。モデルのサンプリングは純粋なノイズ画像から開始し、段階的にノイズを継続的に除去して最終的に鮮明な画像を取得する必要があります。このプロセスでは、モデルは高品質の画像を取得するために少なくとも 50 ～ 100 ステップを連続的に計算する必要があるため、画像の生成に必要な時間が他の深層生成モデルの 50 ～ 100 倍となり、モデルの展開が大幅に制限されます。そして実装。
拡散モデルのサンプリングを高速化するために、多くの研究者はハードウェア最適化の観点から始めます。たとえば、Google は JAX 言語を使用して TPU 上でモデルをコンパイルして実行します。 OneFlow チーム [1] は、Stable Diffusion による「1 秒での画像出力」を実現する自社開発のコンパイラを使用しています。これらの手法は 50 ステップのサンプリング アルゴリズム PNDM [2] に基づいており、ステップ数が減るとサンプリング効果が急激に低下します。
つい数日前、この記録が更新されました。 Stable Diffusion の公式 Demo[3] アップデートでは、8 枚の画像をサンプリングする時間が、元の 8 秒から 4 秒に直接短縮されたことが示されています。 2倍の速さですよ！
OneFlow チームは、自社開発の深層学習コンパイラ技術に基づいており、サンプリング効果を損なうことなく以前の「OneFlow」を変換することに成功しました。 . 「数秒で写真が表示されます」は「0.5秒で写真が表示されます」に短縮されました！ GPU で 0.5 秒以内に高解像度の画像を取得します。関連作品は[1]に掲載されています。
実際、これらの研究の中核となる原動力は、清華大学の Zhu Jun 教授率いる TSAIL チームによって提案された、拡散モデル用に特別に設計された効率的なソルバーである DPM ソルバーから来ています。フィルター: このアルゴリズムは追加のトレーニングを必要とせず、離散時間と連続時間の両方の拡散モデルに適しており、20 ～ 25 ステップ以内でほぼ収束でき、わずか 10 ～ 15 ステップで非常に高品質のサンプリングを取得できます。安定拡散では、25 ステップ DPM ソルバーは 50 ステップ PNDM よりも優れたサンプリング品質を達成できるため、サンプリング速度は直接 2 倍になります。
プロジェクト リンク:
拡散モデルは、継続的に追加する順方向プロセスを定義します。画像は徐々にガウス ノイズに変換され、その後、逆のプロセスが定義されて、ガウス ノイズから徐々にノイズが除去されて鮮明な画像になり、サンプルが取得されます。 ## サンプリング プロセス中に、追加のノイズが追加されるかどうかに応じて、拡散モデルは 2 つのカテゴリに分類できます。1 つは拡散確率微分方程式モデル (Diffusion SDE)、もう 1 つは拡散常微分方程式 (Diffusion ODE) です。両方のモデルのトレーニング目的関数は同じです。「ノイズ予測ネットワーク」は、ノイズによる平均二乗誤差を最小限に抑えることによってトレーニングされます。 Diffusion SDE のサンプリング プロセスは、次の確率微分方程式を離散化するとみなすことができます:
そして、DDPM[5] が [4] で証明されています。 ] は上記の SDE の一次離散化です。
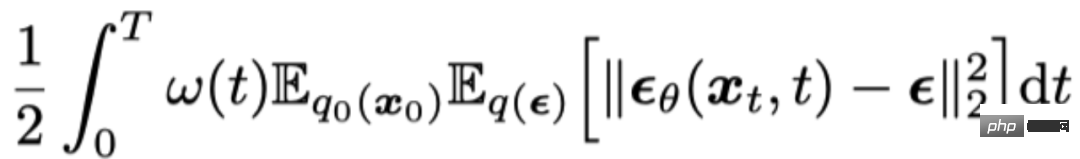拡散 ODE に基づくサンプリング プロセスは、次の常微分方程式を離散化するとみなすことができます。
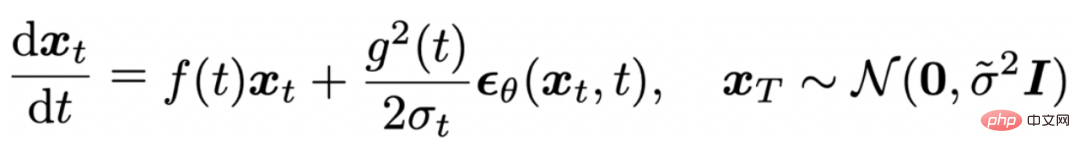
そして、DDIM[7] が上記の ODE の一次離散化であることが [6] で証明されています。
ただし、これらの一次離散化手法は収束が非常に遅く、高品質の画像を取得するには、拡散モデルのサンプリングに通常 100 ～ 1000 回の連続計算が必要です。通常、拡散モデルのサンプリングを高速化するために、研究者は古典的なルンゲ・クッタ法 (RK45) などの拡散 ODE の高次ソルバーを使用してプロセスを高速化します。これは、ODE が追加のランダム性をもたらさないためです。 . . のように、離散化ステップ サイズは比較的大きくなる可能性があります。時間 s での解が与えられた後、Runge-Kutta 法は次の積分の離散化に基づいています:
このような離散化は拡散 ODE を扱います。全体として、ブラック ボックスは ODE の既知の情報を失い、50 ステップ未満で収束するのは困難です。
DPM-Solver は、拡散 ODE の半線形構造に基づいており、正確かつ分析的な計算を通じて、 ODE の線形項を取得すると、次のことが得られます。
残りの積分項は、時間に関する複素積分です。しかし、DPM ソルバーの提案者は、log-SNR (対数信号対雑音比) を代入することで、この積分が非常に簡単な形式で取得できることを発見しました。
残りの積分は、ノイズ予測モデルに関する指数関数的に重み付けされた積分です。ノイズ予測モデルに対してテイラー展開を実行することで、積分の推定値を取得できます。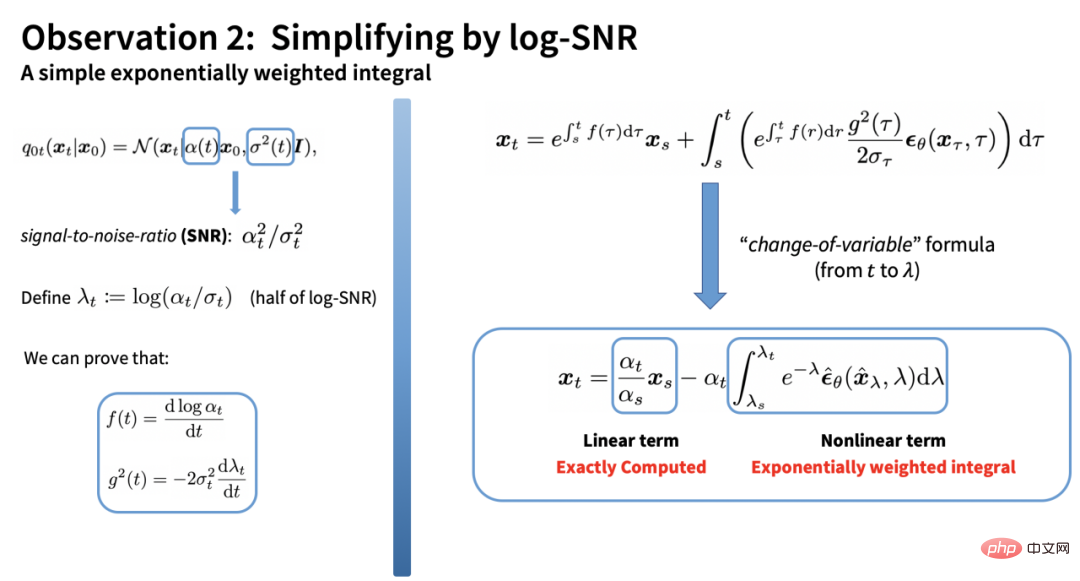
この推定値には 2 つの項目があります。1 つは次のとおりです。完全な導関数部分 (ベクトル) と他の項は係数部分 (スカラー) です。 DPM ソルバーのもう 1 つの中心的な貢献は、部分ごとに積分することで係数を分析的に計算できることです:
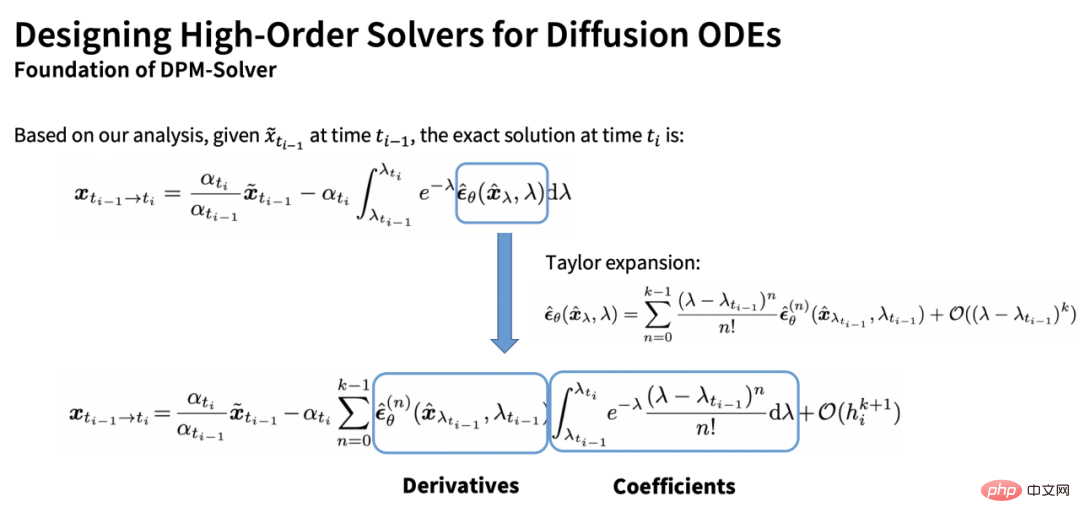
一方、残りの合計微分部分は次のとおりです。従来の ODE ソルバーの数値手法で近似します (微分演算なし):
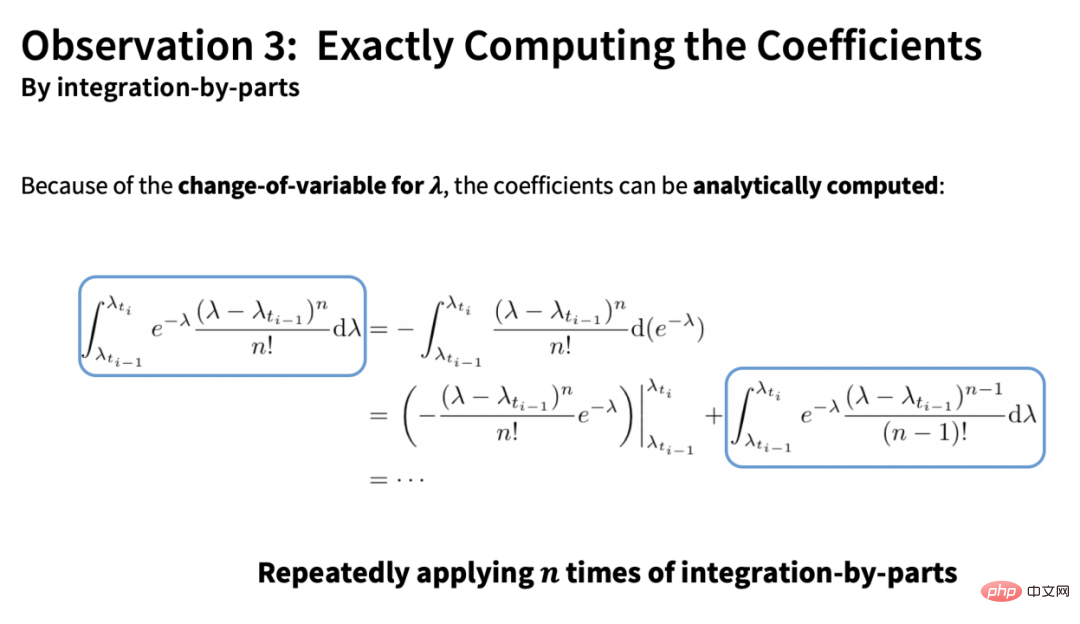
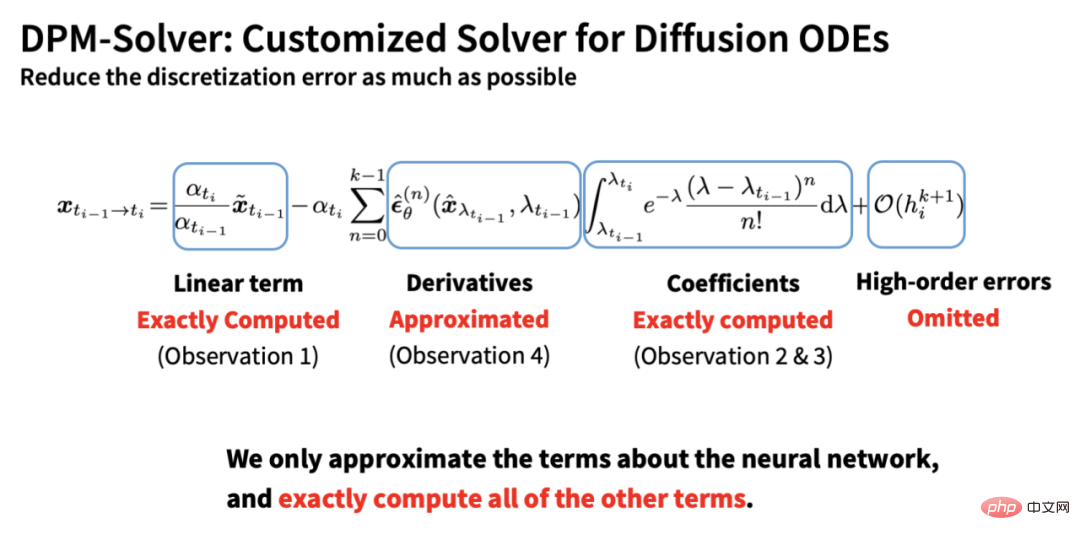
上記の 4 点に基づいて、DPM-Solver は次のことを行います。すべての既知の項をできるだけ正確に計算するために、ニューラル ネットワーク部分のみが近似され、離散化誤差が最小限に抑えられます。この導出により、DDIM が本質的に DPM ソルバーの一次形式であることがわかります。これは、ステップ数が少ない場合でも DDIM が良好な加速効果を達成できる理由も説明できます。
実験では、DPM ソルバーは他のサンプリング アルゴリズムをはるかに上回る加速効果を達成し、わずか 15 ～ 20 ステップでほぼ収束しました。
そして、論文の定量的結果は、DPM ソルバーによって導入される追加の計算量が完全に無視できることを示しています。つまり、ステップ数に対する加速効果は、時間に対する加速効果に正比例します。 、25 ステップに基づく DPM ソルバー モデルと安定拡散モデルのサンプリング速度は直接 2 倍になります。たとえば、次の図は、ステップ数の変化に応じて、さまざまなサンプリング アルゴリズムが安定拡散に及ぼす影響を示しています。DPM ソルバーが 10 ～ 15 ステップで非常に高品質のサンプリングを取得できることがわかります。
#DPM ソルバーの使用
公式コードは 4 つの拡散モデルをサポートしています:
# また、無条件サンプリング、分類子ガイダンス、および分類子なしガイダンスもサポートしています: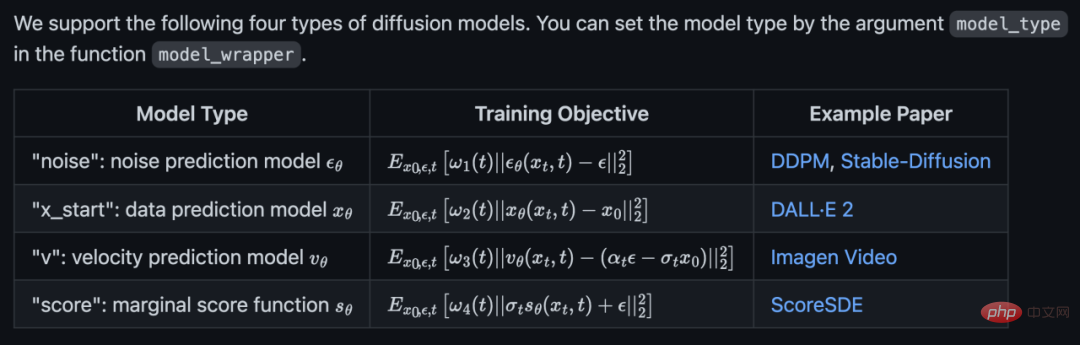
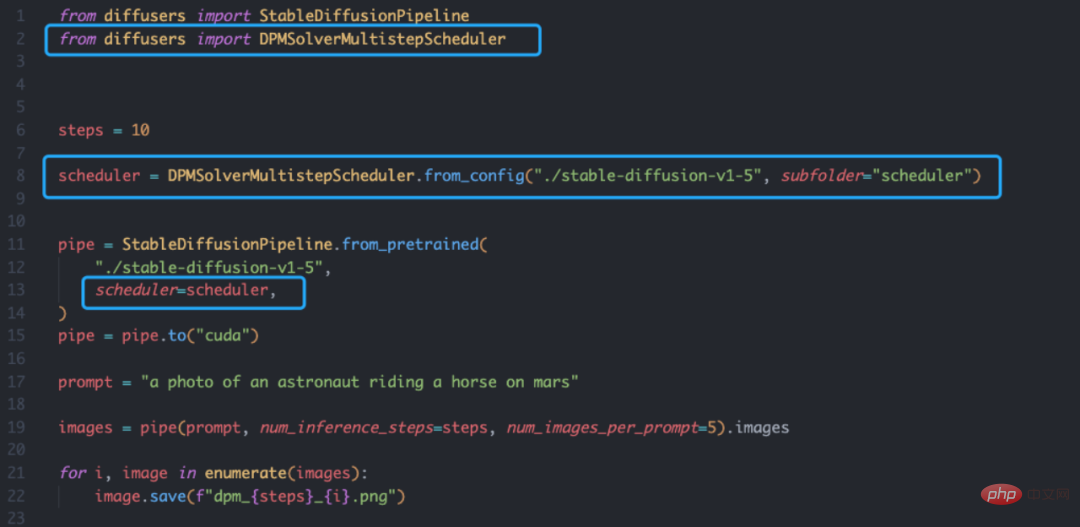
ディフューザー ライブラリに基づく DPM ソルバーも非常にシンプルで、スケジューラを定義するだけで済みます。
さらに、著者チームはオンライン デモも提供しています: https://huggingface.co/spaces/LuChengTHU/dpmsolver_sdm
下の図は 15 ステップです。たとえば、画質が非常に高いことがわかります。
DPM ソルバーに基づいていると思います。拡散モデルのサンプリング速度がボトルネックになることはなくなります。
著者について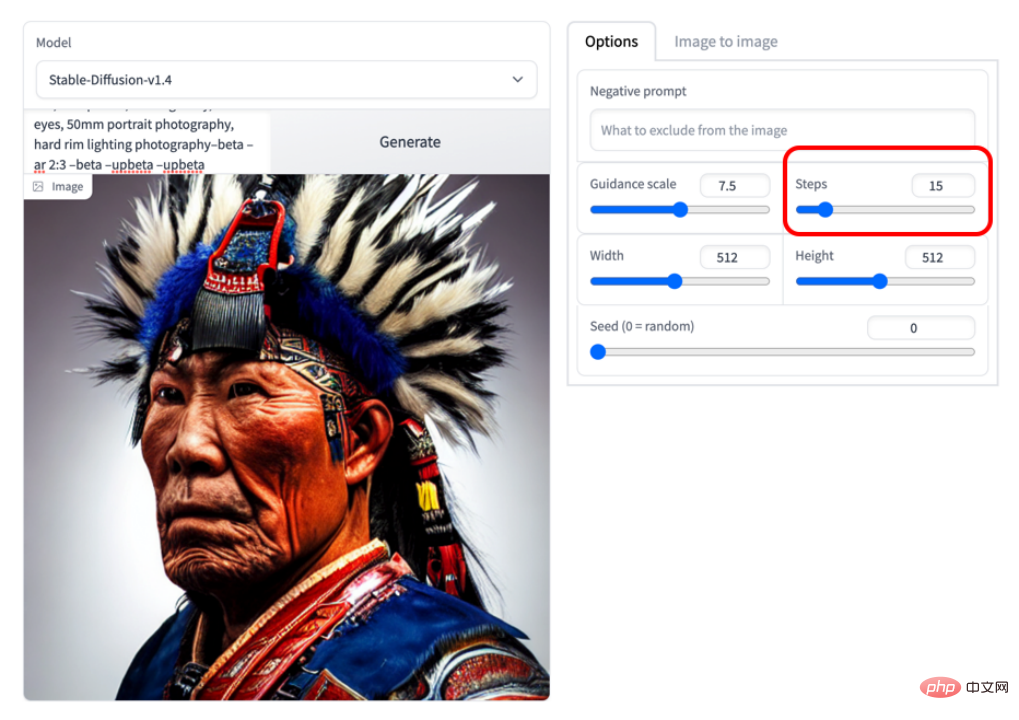
DPM-Solver 論文の最初の著者は、清華大学 TSAIL チームの Lu Cheng 博士です。彼はディスカッションでも次のように書いています。 Zhihu の拡散モデル 拡散モデルの原理の入門書、現在 2,000 件の「いいね！」が付いています: https://www.zhihu.com/question/536012286/answer/2533146567
以上が安定した拡散サンプリング速度が2倍に！わずか 10 ～ 25 ステップの拡散モデル サンプリング アルゴリズムの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
