
この記事では、python に関する関連知識を提供します。主に、アルゴリズムの説明、分析、コード実装など、バブル ソートに関する関連問題を紹介します。以下は、見てみましょう。皆さんのお役に立てれば幸いです。 。

推奨学習: Python ビデオ チュートリアル
# #Bubble Sort (バブル ソート) は、単純な並べ替えアルゴリズムです。ソート対象の配列を繰り返し処理し、一度に 2 つの要素を比較し、順序が間違っている場合はそれらを交換します。配列を走査する作業は、交換が必要なくなるまで繰り返されます。これは、配列がソートされたことを意味します。このアルゴリズムの名前は、小さい要素がスワッピングによって配列の先頭にゆっくりと「浮動」するという事実に由来しています。
#2. アルゴリズム分析
1. 隣接する要素を比較します。最初の値が 2 番目の値よりも大きい場合 (昇順)、両方を入れ替えます。実行プロセスを理解したところで、GIF の実装を見てみましょう
#2. 隣接する要素の各ペアについて、最初の最初のペアから最後の最後のペアまで同じことを行います。このステップが完了すると、最後の要素が最大の数値になります。
#3. 最後の要素を除くすべての要素に対して上記の手順を繰り返します。
4. 数値のペアがなくなるまで、要素を減らして上記の手順を繰り返します。比較する必要があります。
次に、n-1 回のバブリング処理を実行する必要があり、各回の対応する比較回数は次の図に示すとおりです。
3. GIF 表示
:
4. コードの実装
実行結果:
実装コード:
import timepop_list = [19, 14, 10, 4, 15, 26, 20, 96]print("没排序前的列表为:", pop_list)# 记录开始时间start = time.time()# 外层循环控制轮数for i in range(len(pop_list) - 1): # 内层循环控制比较次数 for j in range(len(pop_list) - i - 1): # 如果前一个数字比后一个数字大,就交换位置 if pop_list[j] > pop_list[j + 1]: # python特有交换位置方式 pop_list[j], pop_list[j + 1] = pop_list[j + 1], pop_list[j]print("排序好的列表为:", pop_list)# 记录结束时间end = time.time()print("算法总耗时:", end - start)ログイン後にコピー
5. アルゴリズムのアップグレード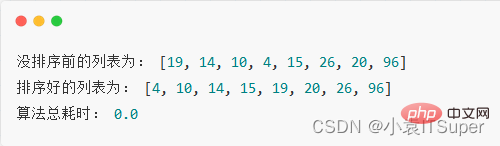
実行結果:
実装コード:import timedef bubble_sort(pop_list): for j in range(len(pop_list) - 1, 0, -1): count = 0 for i in range(0, j): if pop_list[i] > pop_list[i + 1]: pop_list[i], pop_list[i + 1] = pop_list[i + 1], pop_list[i] count += 1 if count == 0: returnpop_list = [19, 14, 10, 4, 15, 26, 20, 96]print("没排序前的列表为:", pop_list)# 记录开始时间start = time.time()bubble_sort(pop_list)print("排序好的列表为:", pop_list)# 记录结束时间end = time.time()print("算法总耗时:", end - start)ログイン後にコピー
Python ビデオ チュートリアル推奨学習:
- 最適な時間計算量:
O(n)(つまり、1 回通過した後、交換できるものは何もありません。要素、並べ替えは終了します。)- # 最悪の時間複雑さ: O(n^2)
- #安定性 : 安定しています
- # 並べ替え分析: 並べ替えられる配列には 8 つの数値があります。並べ替えの最初のラウンドで 7 つの比較が行われ、7 つの比較が行われました。 2 回目のソートでは比較が行われ、6 回の比較が行われ、最終ラウンドでは 1 回の比較が行われました。
- 配列要素の合計数が N の場合、必要な比較の合計数は次のとおりです: (N-1) (N-2) ( N-3 ) ...1=N*(N-1)/2
- アルゴリズムは約 N^2/ を実行します。 2
#交換と比較の回数は N^2 に比例します。big O 表記では定数が無視されるため、バブルソートの時間が複雑になります。 . 次数はの比較。データは前の要素が後の要素より大きい場合にのみ交換されるため、スワップの数は比較の数よりも少なくなります。データがランダムで、データの約半分を交換する必要がある場合、交換回数はN^2/4です (ただし、最悪の場合、最初のデータが逆の順序である場合、比較ごとに交換が必要です)。
- O(N^2) です。
以上がPython バブル ソート アルゴリズムの詳細な図による説明の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。