フロントエンドインタビュー: 6 つの古典的な並べ替えアルゴリズムの実装、いくつ知っていますか? (アニメーション+ビデオを添付)-jsチュートリアル-php.cn

この記事では、6 つの古典的な並べ替えアルゴリズムの実装方法を紹介します。一定の参考値があるので、困っている友達が参考になれば幸いです。

フロントエンドインタビュー: 6 つの古典的な並べ替えアルゴリズムの実装、いくつ知っていますか? (アニメーション+ビデオを添付)

#ソートアルゴリズムはインタビューで高頻度に検査されるポイントであり、これに習熟する必要があります。この記事では、最も古典的で一般的に使用されている並べ替えアルゴリズムをまとめ、それらをアニメーションやビデオと組み合わせて、より簡単に勝てるように支援したいと考えています。

まず、ソートアルゴリズムの特性に応じて、次の 2 つのカテゴリに分類できます。

フロントエンドインタビュー: 6 つの古典的な並べ替えアルゴリズムの実装、いくつ知っていますか? (アニメーション+ビデオを添付)

比較ソート
非比較ソート

名前が示すように、比較ソートは要素間の比較によってソートされますが、非比較ソートには要素間の比較操作は含まれません。。

比較ソートの時間計算量は O(nlogn) を超えることはできません。これは 非線形ソートとも呼ばれます。

非比較ソートの時間計算量は O(nlogn) を超える可能性があり、線形時間で実行できます (線形ソートとも呼ばれます)。

フロントエンドインタビュー: 6 つの古典的な並べ替えアルゴリズムの実装、いくつ知っていますか? (アニメーション+ビデオを添付)

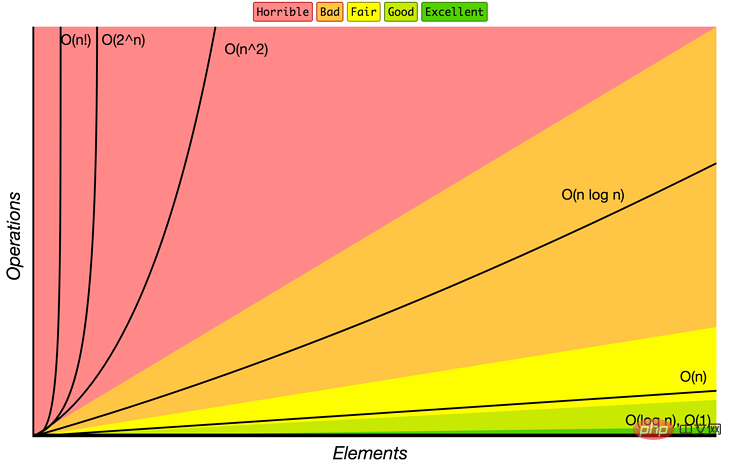
時間計算量をまだ理解していない場合は、JavaScript アルゴリズムの時間と空間の計算量の分析に関するコラムに進んでください。

01 バブルソートバブルソート

バブルソートの視覚化ビデオ:

https://www.reddit.com/r /programming /comments/e55j0i/bubble_sort_visualization/

バブルソート、単純かつ大雑把な 1 文の説明:

バブルソートは 各バブル操作で比較されます。2 つの隣接する要素について 、サイズ関係の要件を満たしているかどうかを確認し、満たしていない場合は交換します。交換が必要なくなるまで、つまりソートが完了するまで繰り返します。

const bubbleSort = function(arr) {
  const len = arr.length
  if (len < 2) return arr
  for (let i = 0; i < len; i++) {
      for (let j = 0; j < len - i - 1; j++) {
          if (arr[j] > arr[j + 1]) {
              const temp = arr[j]
              arr[j] = arr[j + 1]
              arr[j + 1] = temp
          }
      }
  }
  return arr
}

ログイン後にコピー

時間計算量: O(n^2)
空間計算量: O(1)
安定

注: ここでの安定性は、バブルソートが安定した並べ替えアルゴリズムであることを意味します。

安定した並べ替えアルゴリズムとは何ですか?

ソートアルゴリズムの安定性

ソートアルゴリズムの品質を判断するには、実行効率とメモリ消費量のみを使用してください。それが十分でない場合は、並べ替えアルゴリズムのもう 1 つの重要な指標である 安定性 があります。

つまり、 ソート対象のシーケンス内に等しい値を持つ要素があった場合、ソート後も、等しい要素間の元の順序は変わりません。

例:

たとえば、1、9、2、5、8、9 というデータのセットがあるとします。サイズごとに分類すると、1、2、5、8、9、9 になります。

このデータセットには 9 が 2 つあります。特定の並べ替えアルゴリズムで並べ替えた後、2 つの 9 の順序が変わらない場合、この並べ替えアルゴリズムを 安定並べ替えアルゴリズムと呼びます# # ＃。 それ以外の場合、
不安定な並べ替えアルゴリズムになります。

バブルソートの最適化

上記のコードも最適化できます。特定のバブル操作で

データ交換が行われていない場合、それはデータ交換が行われていることを意味します。完全な順序を達成するために、後続のバブリング操作を実行し続ける必要はありません。 <div class="code" style="position:relative; padding:0px; margin:0px;"><pre class="brush:js;toolbar:false;">const bubbleSort = function(arr) { const len = arr.length let flag = false if (len < 2) return arr for (let i = 0; i < len; i++) { flag = false // 提前退出冒泡循环的标志 for (let j = 0; j < len - i - 1; j++) { if (arr[j] > arr[j + 1]) { const temp = arr[j] arr[j] = arr[j + 1] arr[j + 1] = temp flag = true // 表示有数据交换 } } if (!flag) break // 没有数据交换，提前退出 } return arr }</pre><div class="contentsignin">ログイン後にコピー</div></div>

02 挿入ソート

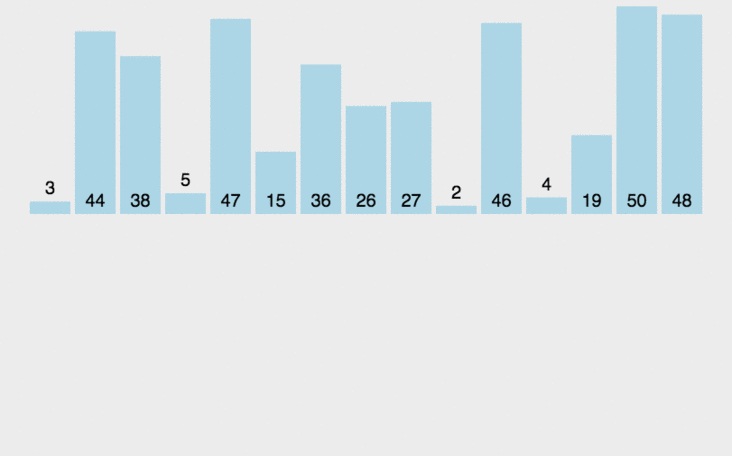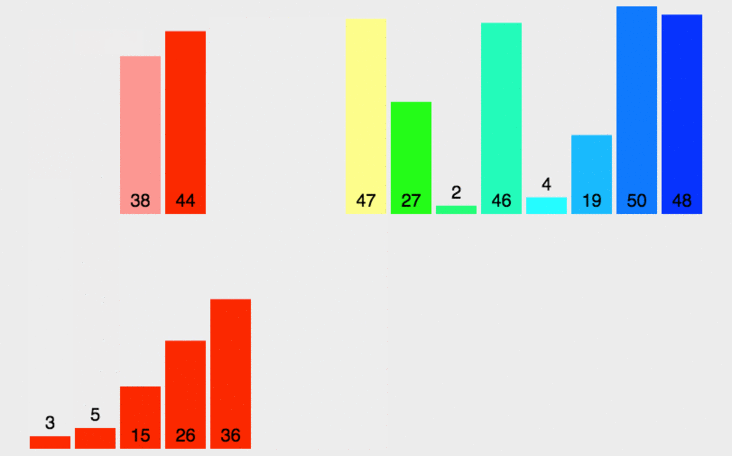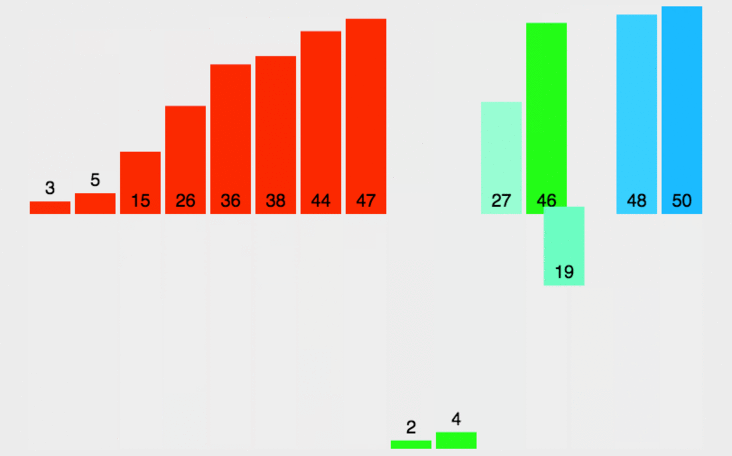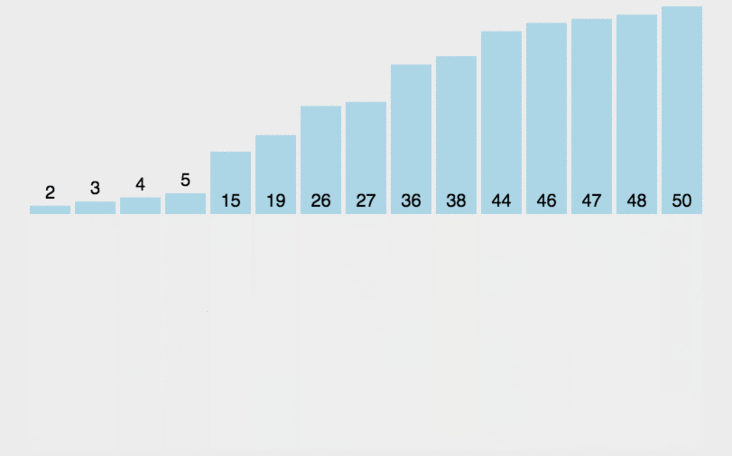フロントエンドインタビュー: 6 つの古典的な並べ替えアルゴリズムの実装、いくつ知っていますか? (アニメーション+ビデオを添付) 挿入ソート名前が示すように、ソートされていないデータに対して、スキャンでソートされたシーケンスを後ろから前に向かって、対応する位置を見つけて挿入し、ソートされたシーケンス内の要素の順序を保ちます。

i が 1 に等しいところからトラバースを開始し、現在の要素 curr を取得して、前の要素と比較します。

前の要素が現在の要素より大きい場合は、前の要素を現在の要素と交換し、並べ替えられていないシーケンス内の要素が空になり並べ替えが完了するまでループを続けます。

const insertSort = function(arr) {
    const len = arr.length
    let curr, prev
    for (let i = 1; i < len; i++) {
        curr = arr[i]
        prev = i - 1
        while (prev >= 0 && arr[prev] > curr) {
            arr[prev + 1] = arr[prev]
            prev--
        }
        arr[prev + 1] = curr
    }
    return arr
}

ログイン後にコピー

時間計算量: O(n^2)

空間計算量: O(1)
安定

03 選択ソート

選択ソートの視覚化ビデオ:

https://www.reddit.com/r/programming/comments/e5md13/selection_sort_visualization /

選択ソートは挿入ソートに似ており、ソートされたシーケンスとソートされていないシーケンスにも分けられます。

しかし、選択による並べ替えは、

配列の先頭に最小の要素を格納し、その後、残りの未並べ替えのシーケンスから最小の要素を見つけて、それを並べ替えられたシーケンスの後に配置します

。並べ替えが完了するまで続きます。 <div class="code" style="position:relative; padding:0px; margin:0px;"><pre class="brush:js;toolbar:false;">const selectSort = function(arr) { const len = arr.length let temp, minIndex for (let i = 0; i < len - 1; i++) { minIndex = i for (let j = i + 1; j < len; j++) { if (arr[j] <= arr[minIndex]) { minIndex = j } } temp = arr[i] arr[i] = arr[minIndex] arr[minIndex] = temp } return arr }</pre><div class="contentsignin">ログイン後にコピー</div></div>

時間計算量: O(n^2)

空間計算量: O(1)
不安定

04 マージソート

フロントエンドインタビュー: 6 つの古典的な並べ替えアルゴリズムの実装、いくつ知っていますか? (アニメーション+ビデオを添付) 分割統治法の典型的な応用例。征服アルゴリズムは主に再帰に基づいており、再帰を使用して実装するのがより適しています。

処理プロセスは下から上に進み、最初にサブ問題を処理してからそれらをマージします。

<p>如果感觉自己对递归掌握的还不是很透彻的同学，可以移步我的这篇专栏你真的懂递归吗？。</p><p>顾名思义，分而治之。一般分为以下三个过程：</p><ul style="max-width:90%"><li><p>分解：将原问题分解成一系列子问题。</p></li><li><p>解决：递归求解各个子问题，若子问题足够小，则直接求解。</p></li><li><p>合并：将子问题的结果合并成原问题。</p></li></ul><p>归并排序就是将待排序数组不断二分为规模更小的子问题处理，再将处理好的子问题合并起来，这样整个数组就都有序了。</p><div class="code" style="position:relative; padding:0px; margin:0px;"><pre class="brush:js;toolbar:false;">const mergeSort = function(arr) { const merge = (right, left) => { const result = [] let i = 0, j = 0 while (i < left.length && j < right.length) { if (left[i] < right[j]) { result.push(left[i++]) } else { result.push(right[j++]) } } while (i < left.length) { result.push(left[i++]) } while (j < right.length) { result.push(right[j++]) } return result } const sort = (arr) => { if (arr.length === 1) { return arr } const mid = Math.floor(arr.length / 2) const left = arr.slice(0, mid) const right = arr.slice(mid, arr.length) return merge(mergeSort(left), mergeSort(right)) } return sort(arr) }</pre><div class="contentsignin">ログイン後にコピー</div></div><ul><li>时间复杂度: O(nlogn)</li><li>空间复杂度: O(n)</li><li>稳定</li></ul><h2><strong>05 快速排序 Quick Sort</strong></h2><blockquote><p>快速排序可视化视频：</p><p>https://www.reddit.com/r/dataisbeautiful/comments/e9fb2k/oc_quicksort_visualization/</p></blockquote><p>快速排序也是分治法的应用，<code>处理过程是由上到下的，先分区，然后再处理子问题。

快速排序通过遍历数组，将待排序元素分隔成独立的两部分，一部分记录的元素均比另一部分的元素小，则可以分别对这两部分记录的元素继续进行排序，直到排序完成。

这就需要从数组中挑选出一个元素作为 基准(pivot)，然后重新排序数列，将元素比基准值小的放到基准前面，比基准值大的放到基准后面。

然后将小于基准值的子数组(left)和大于基准值的子数组(right)递归地调用 quick 方法，直到排序完成。

const quickSort = function(arr) {
    const quick = function(arr) {
        if (arr.length <= 1) return arr
        const len = arr.length
        const index = Math.floor(len >> 1)
        const pivot = arr.splice(index, 1)[0]
        const left = []
        const right = []
        for (let i = 0; i < len; i++) {
            if (arr[i] > pivot) {
                right.push(arr[i])
            } else if (arr[i] <= pivot) {
                left.push(arr[i])
            }
        }
        return quick(left).concat([pivot], quick(right))
    }
    const result = quick(arr)
    return result
}

ログイン後にコピー

时间复杂度: O(nlogn)
空间复杂度: O(nlogn)
不稳定

06 堆排序 Heap Sort

フロントエンドインタビュー: 6 つの古典的な並べ替えアルゴリズムの実装、いくつ知っていますか? (アニメーション+ビデオを添付)

堆排序相比其他几种排序代码会有些复杂，不过没关系，我们先来看一些前置知识，可以帮助我们更好的理解堆排序。

堆排序顾名思义就是要利用堆这种数据结构进行排序。堆是一种特殊的树，满足以下两点就是堆：

堆是一个完全二叉树
堆中每一个节点的值都必须大于等于(或小于等于)其子树中的每个节点的值

每个节点的值都大于等于子树中每个节点值的堆，叫做大顶堆，每个节点的值都小于等于子树中每个节点值的堆，叫做小顶堆。

也就是说，大顶堆中，根节点是堆中最大的元素。小顶堆中，根节点是堆中最小的元素。

如果你对树这种数据结构还不是很了解，可以移步我的这篇专栏“树”业有专攻

堆如果用一个数组表示的话，给定一个节点的下标 i (i从1开始)，那么它的父节点一定为 A[i / 2]，左子节点为 A[2i]，右子节点为 A[2i + 1]。

堆排序包含两个过程，建堆和排序。首先构建一个大顶堆，也就是将最大值存储在根节点(i = 1)，每次取大顶堆的根节点与堆的最后一个节点进行交换，此时最大值放入了有效序列的最后一位，并且有效序列减 1，有效堆依然保持完全二叉树的结构，然后进行堆化成为新的大顶堆。重复此操作，直到有效堆的长度为 0，排序完成。

const heapSort = function(arr) {
    buildHeap(arr, arr.length - 1)
    let heapSize = arr.length - 1 // 初始化堆的有效序列长度
    for (let i = arr.length - 1; i > 1; i--) {
        swap(arr, 1, i) // 交换堆顶元素与最后一个有效子元素
        heapSize-- // 有效序列长度减 1
        heapify(arr, heapSize, 1) // 堆化有效序列
    }
    return arr
}

// 构建大顶堆
const buildHeap = function(items, heapSize) {
    // 从后往前并不是从序列的最后一个元素开始，而是从最后一个非叶子节点开始，这是因为，叶子节点没有子节点，不需要自上而下式堆化。
    // 最后一个子节点的父节点为 n/2 ，所以从 n/2 位置节点开始堆化
    for (let i = Math.floor(heapSize / 2); i >= 1; i--) {
        heapify(items, heapSize, i)
    }
}
// 堆化
const heapify = function(arr, heapSize, i) {
    while (true) {
        let maxIndex = i
        if (2 * i <= heapSize && arr[i] < arr[i * 2]) {
            maxIndex = i * 2
        }
        if (2 * i + 1 <= heapSize && arr[maxIndex] < arr[i * 2 + 1]) {
            maxIndex = i * 2 + 1
        }
        if (maxIndex === i) break
        swap(arr, i, maxIndex)
        i = maxIndex
    }
}

// 交换工具函数
const swap = function(arr, i, j) {
    let temp = arr[i]
    arr[i] = arr[j]
    arr[j] = temp
}

ログイン後にコピー