時変システムと時不変システムの違いは何ですか?

時変システムと時不変システムの違い: 時変システムの 1 つ以上のパラメーター値は時間とともに変化するため、全体の特性も時間とともに変化します。時不変システムとは、時間とともに変化しないシステムの応答の挙動は、入力信号の挙動とシステムの特性にのみ依存し、入力信号が印加された時間とは関係がありません。

このチュートリアルの動作環境: Windows 7 システム、Dell G3 コンピューター。

システムにパラメータが時間とともに変化するコンポーネントが含まれているかどうかに応じて、自動制御システムは時間変動システムと定常システムの 2 つのカテゴリに分類できます。

定常システムは時不変システムとも呼ばれ、次のような特徴があります。 システム自体の特性 (質量、慣性モーメントなど)時間が経っても変化しません。具体的には、システム応答の挙動は入力信号の挙動とシステムの特性にのみ依存し、入力信号が適用された瞬間とは何の関係もありません。入力が遅延すると、出力 y(t) τ がシステムに適用された後、u(t-τ) によって生成される出力は y(t-τ) になります。

定常システムは時不変システムとも呼ばれます

つまり、システムは時間とともに変化しません。具体的には、システム応答の挙動は入力信号の挙動とシステムの特性にのみ依存し、入力信号が印加された瞬間とは関係ありません。つまり、時間 t1 に u を入力すると出力は y になり、時間 t2 で u を入力しても出力値は y

になります。 ##時変システム

1 つ以上のパラメータ値が時間の経過とともに変化し、したがって全体の特性も時間の経過とともに変化するシステム。

ロケットは時間変化システムの典型的な例です。飛行中、その質量は燃料の消費により時間の経過とともに減少します。もう 1 つの一般的な例はマニピュレーターです。対応する軸の周りの各関節の慣性モーメントは、時間を独立変数とする複素関数です。

時間不変システムは、出力が時間とともに直接変化しないシステムです。

#入力信号 # が出力 y(t) を生成する場合、入力信号の時間遅延に対して # は出力 y(t) を取得します。同じ時間遅延。

#システムの伝達関数が時間の関数でない場合、この特性を満たすことができます。この機能は、回路図の用語で説明することもできます。

#システムが時間不変であるかどうかを判断する方法を示すために、2 つのシステムを見てみましょう:

システム A:

##システム B:

# #システム A は x(t) と y(t) に加えて t に明示的に依存するため、時間変動システムですが、システム B は時間

数学的分析:

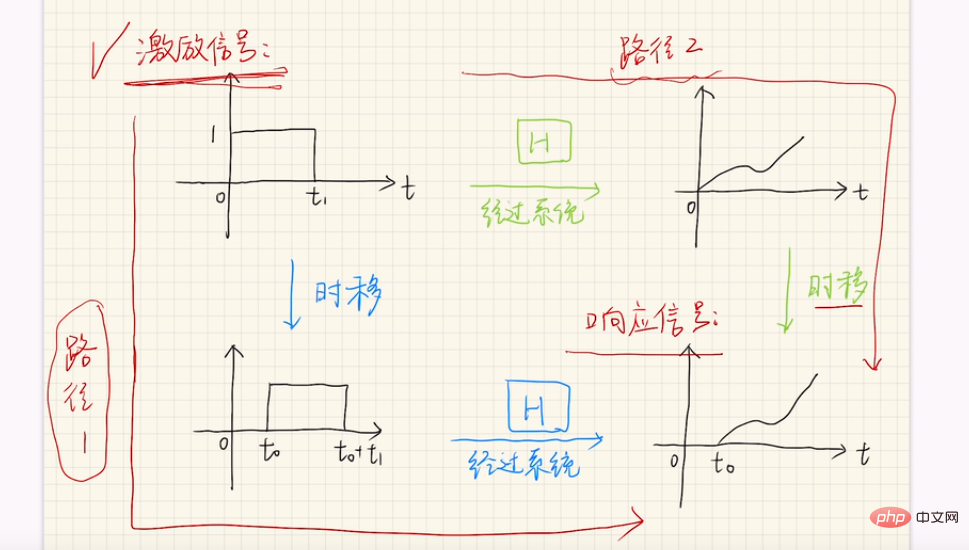
あるシステムの入力が u(t) で、対応する出力が y(t) であると仮定します。

入力が τ 遅れた後、つまり入力が u(t-τ) の場合、それに応じて出力も τ 遅れた場合、つまり出力はが y(t-τ) である場合、この系は定常系になります。
つまり、入力信号 u(t) が最初に τ だけ u(t-τ) にタイムシフトされ、次にシステム変換 H[■] が実行されて値 H[u(t-τ) が得られます。 )];

端的に言うと、システムは最初の瞬間から T 時間の間動作し、この期間中の入力と出力は対応する軌跡を持ちます。

時刻 T におけるこのシステムの状態を初期時刻から T 時間だけ再実行すると、入力は初期時刻からの形式が変化します。は前と同じです、見てください 出力は前と同じですか?

(たとえば、ロケットを例にとると、入力は次のものを参照します押すエネルギー、出力は加速度を指します;

通常の状態でロケットが初めて打ち上げられるとき、T 時間実行すると、エネルギー、加速度、時間を入力することで三次元曲線Q1を描くことができます。

T時間に1回目と同じ状態で2回目のロケットが打ち上げられます。 T 時間走行すると（入力エネルギーの時間変化は 1 回目と同じ）、このときの入力エネルギーと加速度出力、時間の変化は別の 3 次元曲線 Q2 を描きます。 Q1 と Q2 は出力加速度において重なりません (時間 T での質量が小さくなるため必ず変化します))

入力信号 u(t) が最初に適用されます。システム変換 H[■] を適用して y(t) を取得し、タイム シフトによって得られた値 y(t-τ) は H[u(t-τ) )]=y(t-τ) に等しくなります。
例:
1. システム y(t)=cos[u(t)], t>0 が時不変システムであるかどうかを判断します:
1). 入力信号 u(t) , 最初に進みます 時間シフトは u(t-τ) であり、システム変換によって得られる値は cos[u(t-τ)], t>0;
2). 入力信号 u(t),最初に cos[u(t)] としてシステム変換を実行し、次に時間シフトによって得られる値は cos[u(t-τ)]、t>0;
が等しいため、システムは時間不変です。システム。
2. システム y(t)=u(t)・cost が時不変システムであるかどうかを判断します:
1). 信号 u(t) を入力し、最初に u(t への時間シフトを実行します) -τ), システム変換によって得られる値は u(t-τ)・コスト, t>0;
2). 入力信号 u(t)、まず u(t)・コストへのシステム変換を実行します。得られた値は u(t-τ)・cos(t-τ)、t>0;
u(t-τ)・cost≠u(t-τ)・cos(t- τ)、つまり、システムは時間変化するシステムです。

私たちが最終的に注目するのは、最終的な画像が

注: 上記の解析方法は、方法 I を使用して定常システムであるかどうかをテストするためにも使用できます。つまり、u が t1 に入力され、出力が y であると仮定し、u が t2 に入力され、出力が であると仮定します。値がまだ y

以上が時変システムと時不変システムの違いは何ですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。