バランス二分木と二分ソート木の間に直接の関係はありませんが、二分ソート木の検索効率は二分木の形状に関係します。このように均一であること 二分木はバランス二分木と呼ばれます。

1. バイナリソートツリー
バイナリ ソート ツリー、
バイナリ検索ツリー (バイナリ検索ツリー)、バイナリ検索ツリーとも呼ばれます。
バイナリ ソート ツリーは、空のツリーであるか、次のプロパティを持つバイナリ ツリーです。
左のサブツリーが空でない場合、左のサブツリー上のすべてのノードの値はそのルート ノードの値より小さくなります。- 右のサブツリーが空でない場合は、空でない場合、右のサブツリー上のすべてのノードの値がそのルート ノードの値より大きい;
- 左と右のサブツリーもそれぞれバイナリ ソート ツリーです。
-
下の図に示すように、これはバイナリ ソート ツリーです。
 バイナリ ソート ツリーで順序トラバーサルを実行して、キーワード シーケンスでソートされた結果を取得します。たとえば、上図を順番に走査すると、順序付けられたシーケンス 10、42、45、55、58、63、67、70、83、90、98
バイナリ ソート ツリーで順序トラバーサルを実行して、キーワード シーケンスでソートされた結果を取得します。たとえば、上図を順番に走査すると、順序付けられたシーケンス 10、42、45、55、58、63、67、70、83、90、98
を取得できます。 #バイナリ ソート ツリーの検索分析
バイナリソートツリー検索 最悪の場合、必要な検索時間はツリーの
深さに依存します
:- バイナリソートツリーがフルバイナリツリーに近い場合、その深さは#2n したがって、最悪の場合の検索時間は O( #log2n log_2n n)、これは二分探索と同じ桁です。 次の図に示すように、二分木が 単一分岐木 を形成する場合、その深さは n であり、最悪の場合の検索時間は O(n) になります。順次検索と同じ桁の大きさです。 Soバイナリソートツリー検索で高速な検索速度を確保するには、バイナリツリーが完全なバイナリツリーに近いか、左右のサブツリーの深さがバイナリ ツリーの各ノードは可能な限り等しい 2. バランスの取れたバイナリ ツリー上記の分析を通じて、バイナリの検索効率が向上していることがわかります。ソートツリーは二分木の形状に関係しており、二分ソート木の形状が均一であることが望まれ、そのような二分木はバランス二分木と呼ばれます。
-
バランス バイナリ ツリーの定義
バランス バイナリ ツリー (バランス バイナリ ツリー)、空のツリー、または次のプロパティがあります:
- その左と右のサブツリー間の深さの差の絶対値は 1 を超えません;
- その左と右のサブツリーもそれぞれバランスの取れたバイナリ ツリーです。
バイナリ ツリー ノードの左側のサブツリーの深さから右側のサブツリーの深さを引いたものは、バランス係数 BF と呼ばれます。この場合、バランス係数のバランスを取ることのみが可能です。バイナリ ツリー上のすべてのノード。それらは -1、0、1 です。下の図の左側はバランスの取れたバイナリ ツリー、右側はアンバランスのバイナリ ツリーです。
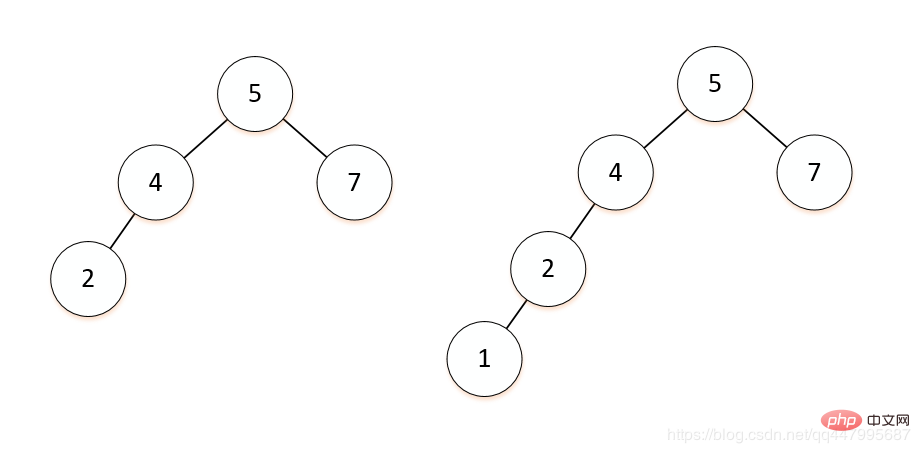
バランスの取れた二分木上のノードの左右のサブツリーの深さの差は 1 を超えないため、その深さは完全なノードの深さと同じであることが証明できます。 n 個のノードを持つバイナリ ツリー#⌊l#og 2n⌋ 1 は同じ桁の大きさです。したがって、平均検索数も ##⌊⌊log #2##n⌋ 1同じ桁です。 バランスの取れたバイナリ ツリーを構築するために、Georgii M. Adelson-Velskii と Evgenii M. Landis は、バイナリのバランスのとれたツリーを動的に維持する方法を提案しました。基本的な考え方は次のとおりです。を挿入する場合は、まずノードの挿入によりツリーのバランスが崩れていないか確認し、崩れている場合には、最も小さい不均衡部分木を見つけ、ソートされたツリーを維持しながら最小の不均衡部分木を調整することで、各ノード間の接続関係が新たな状態を実現します。したがって、このようなバランスのとれたバイナリ ツリーは AVL ツリー と呼ばれます。最小平衡サブツリーとは、挿入されたノードに最も近いノードであり、バランス係数の絶対値が 1 より大きいサブツリー をルート ノードとして指します。 - 最小アンバランス サブツリーを調整するには、一般に 4 つの状況があります。
-
一方向右回転 (LL タイプ): 下の図に示すように、挿入位置は左サブツリーの左サブツリーであり、左サブツリーを軸として単一の右回転を実行します。ノードの横の数字はノードのバランス係数で、I ノードが現在挿入されているノードです (I ノードが中央にある場合、I ノードは左の子または右の子のいずれかである可能性があることを意味します)。
注 LL タイプは、中央のノードを軸として回転します。ここで I が BL の左の子である理由は、B-BL-I を LL タイプとして使用できないためです。 A ノードは I ノードに最も近い バランスです 因子の絶対値 > 1 を持つサブツリーの場合、他のノードのバランス因子の絶対値は 1 を超えません; 同様に、I が正しい子の場合、 BL、B-BL-I は LR タイプとはみなせません .
2.  一方向左回転(RR タイプ):
一方向左回転(RR タイプ):
位置が右サブツリーであり、右サブツリーが軸である右サブツリーを作成し、単一の左回転を実行しますRR タイプに注意して、中央のノードを軸として回転します。は左右のサブツリーであり、実際の RR タイプには影響しません。原理は上記と同じです。
3.  最初に左、次に右への双方向回転 (LR タイプ): 挿入左のサブツリーの位置にある右のサブツリーを作成し、最初は左へ、次に右への 2 つの回転を実行します。
最初に左、次に右への双方向回転 (LR タイプ): 挿入左のサブツリーの位置にある右のサブツリーを作成し、最初は左へ、次に右への 2 つの回転を実行します。
ノードを左の子として挿入します。なぜ
ができないのかに注意してください。 B-C-IをサブツリーとしてRL型として定義します原理はRR型の説明と同じですLR型の場合R端またはLが挿入ノードに近い端を軸として使用します(下の図に示すように、まず B をルートとしてサブツリーを回転して LL 形状にし、次に A をルートとしてサブツリーを回転するのと同じです)。ノードを右側に挿入します 子:
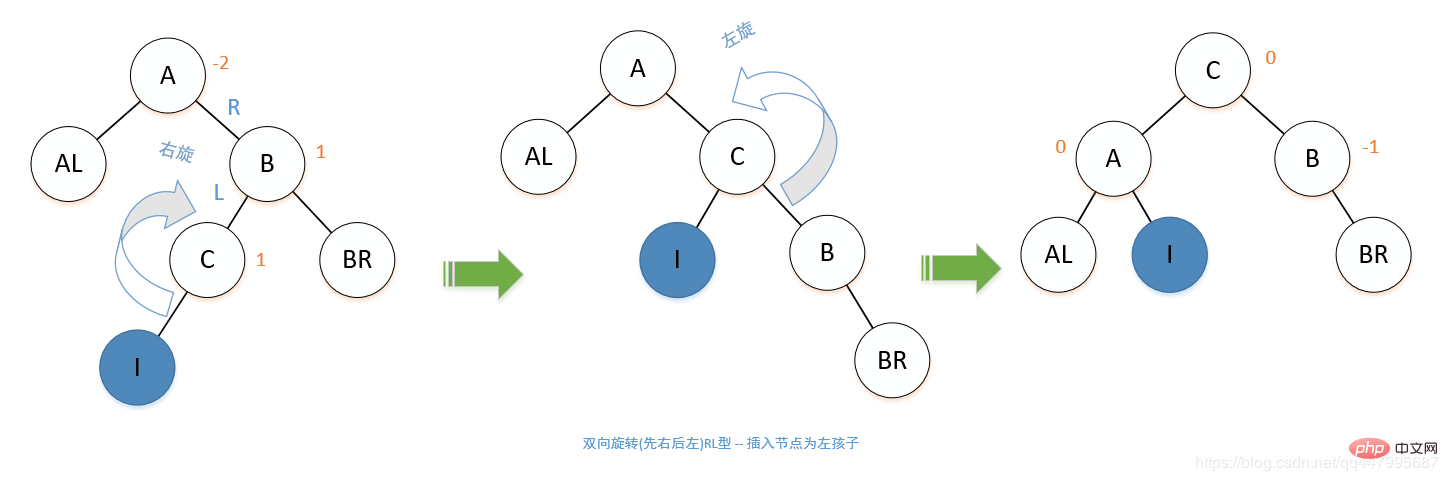
4.  最初に右、次に左への双方向回転 (RL タイプ): 右のサブツリーの位置にある左のサブツリーを挿入し、2 つ作成します調整、最初に右回転、次に左回転。処理状況は LR と同様です。
最初に右、次に左への双方向回転 (RL タイプ): 右のサブツリーの位置にある左のサブツリーを挿入し、2 つ作成します調整、最初に右回転、次に左回転。処理状況は LR と同様です。
 ノードを左の子として挿入します:
ノードを左の子として挿入します:
ノードを右として挿入しますchild:
 上記の結果、バランス係数はタイプと大きな関係があることがわかります。
上記の結果、バランス係数はタイプと大きな関係があることがわかります。
挿入したノードに最も近いノードと絶対ノードを使用する必要があります。バランス係数の値 > 1 をルート ノードのサブツリーとして使用し、それがどのタイプであるかを決定します。下図のように、まず節点2を挿入してLL型にし、全体の右手処理後にバランスをとります。

8、6を順に挿入すると、節点2の絶対値が決まります。ノード 5 のバランス係数は 1 より大きく、RL タイプになります。そのため、最初に 5 をルート ノードとして取得し、そのサブツリー 8 ~ 6 を右回転し (RR タイプになります)、次に 5 をルート ノードとしてツリー全体を左に回転します。 ノード 9 を挿入し続けると、ノード 4 のバランス係数が 1 を超え、RR タイプになるため、4 がルート ノードとなり、全体を左に回します。
以上がバランスの取れたバイナリ ツリーとソートされたバイナリ ツリーの関係の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

 バイナリ ソート ツリーで順序トラバーサルを実行して、キーワード シーケンスでソートされた結果を取得します。たとえば、上図を順番に走査すると、順序付けられたシーケンス 10、42、45、55、58、63、67、70、83、90、98
バイナリ ソート ツリーで順序トラバーサルを実行して、キーワード シーケンスでソートされた結果を取得します。たとえば、上図を順番に走査すると、順序付けられたシーケンス 10、42、45、55、58、63、67、70、83、90、98