コンピュータ サイエンスでは、バイナリ ツリーは、ノードごとに最大 2 つのサブツリーを持つツリー構造です。通常、サブツリーは「左サブツリー」および「右サブツリー」と呼ばれます。バイナリ ツリーは、バイナリ検索ツリーとバイナリ ヒープの実装によく使用されます。

深さ k で 2^k-1 個のノードを持つバイナリ ツリーは、完全バイナリ ツリーと呼ばれます。この種のツリーの特徴は、各レベルのノード数が最大ノード数であることです。バイナリ ツリーでは、最後のレベルを除いて、他のすべてのレベルがいっぱいで、最後のレベルがいっぱいであるか、右側にいくつかの連続したノードが欠落している場合、そのバイナリ ツリーは完全なバイナリ ツリーです。 n 個のノードを持つ完全なバイナリ ツリーの深さは、floor(log2n) 1 です。深さ k の完全なバイナリ ツリーには、少なくとも 2k-1 個のリーフ ノード、最大で 2k-1 個のノードがあります。
ある二分木には次数 2 のノードが 5 つあります。この二分木の葉ノードの数は何ですか?
バイナリ ツリーのリーフ ノードの数と次数 2 のノードの数の関係は次のとおりです: 次数 2 のノードの数 = リーフ ノードの数 -1;
したがって、リーフ ノードの数 = 次数 2 のノードの数 1=6 となります。
展開:
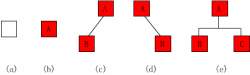
バイナリ ツリーは再帰的に定義され、そのノードは左右のサブツリーに分割されます。論理的には、バイナリ ツリーには 5 つの基本形式があります:
空のバイナリ ツリー - (a) に示す;
ルート ノードが 1 つだけあるバイナリ ツリー - (b) に示す;
左側のサブツリーのみ - (c) に示す;
右側のサブツリーのみ - (d) に示す;
完全なバイナリ ツリー - (e) に示すように。
注: バイナリ ツリーにはツリーと多くの類似点がありますが、バイナリ ツリーはツリーの特殊なケースではありません。
Type
(1) 完全な二分木 - 二分木の高さが h の場合、h 番目の層を除き、他のすべての層のノード数 (1~h) -1) が最大になる 第 h 層には葉ノードがあり、それが左から右に並んでおり、完全な二分木になります。
(2) 完全なバイナリ ツリー - リーフ ノードを除くすべてのノードに左右のサブリーフがあり、リーフ ノードがすべて最下位にあるバイナリ ツリー。
(3) バランス バイナリ ツリー - バランス バイナリ ツリーは、AVL ツリーとも呼ばれます (AVL アルゴリズムとは異なります)。これはバイナリ ソート ツリーであり、次の特性があります: 空のツリーであるか、または左右のサブツリー間の高さの差の絶対値は 1 を超えず、左右のサブツリーは両方ともバランスの取れた二分木です。
さらに関連する知識については、PHP 中国語 Web サイト に注目してください。 !
以上がある二分木には次数 2 のノードが 5 つあります。この二分木の葉ノードの数はいくつでしょうか。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。