JavaScript トピック シリーズの 20 番目で最後の記事、v8 並べ替えソース コードの解釈
v8 は Chrome の JavaScript エンジンであり、配列の並べ替えは JavaScript で完全に実装されています。
ソートに使用されるアルゴリズムは配列の長さに関連しており、配列の長さが 10 以下の場合は挿入ソートが使用され、配列の長さが 10 を超える場合はクイック ソートが使用されます。 (もちろん、この記述は厳密ではありません)。
まず挿入ソートとクイックソートを見てみましょう。
最初の要素を順序付けられたシーケンスとして扱い、配列を走査し、この構築された順序付けされたシーケンスに後続の要素を順番に挿入します。
function insertionSort(arr) {
for (var i = 1; i < arr.length; i++) {
var element = arr[i];
for (var j = i - 1; j >= 0; j--) {
var tmp = arr[j];
var order = tmp - element;
if (order > 0) {
arr[j + 1] = tmp;
} else {
break;
}
}
arr[j + 1] = element;
}
return arr;
}
var arr = [6, 5, 4, 3, 2, 1];
console.log(insertionSort(arr));時間計算量とは、入力値のサイズが無限大に近づくときの状況を調べます。アルゴリズムの基本操作が繰り返される回数は、問題のサイズ n の関数です。
最良の場合: 昇順の配列、時間計算量: O(n)
最悪の場合: 降順の配列、時間計算量: O(n²)
安定性は同じ意味です要素がまだ維持されているかどうか並べ替え後の相対位置。
不安定な並べ替えアルゴリズムの場合は、その不安定性を説明するために例を示すだけですが、安定した並べ替えアルゴリズムの場合は、安定した特性を取得するためにアルゴリズムを分析する必要があることに注意してください。
たとえば、[3, 3, 1] は、並べ替え後も [3, 3, 1] のままですが、実際には 2 番目の 3 が最初の 3 より前にある場合、これは不安定な並べ替えアルゴリズムです。
挿入ソートは安定したアルゴリズムです。
配列がソートされようとしている場合、または問題のサイズが比較的小さい場合は、挿入ソートの方が効率的です。 v8 が配列の長さが 10 以下の場合に挿入ソートを使用するのはこのためです。
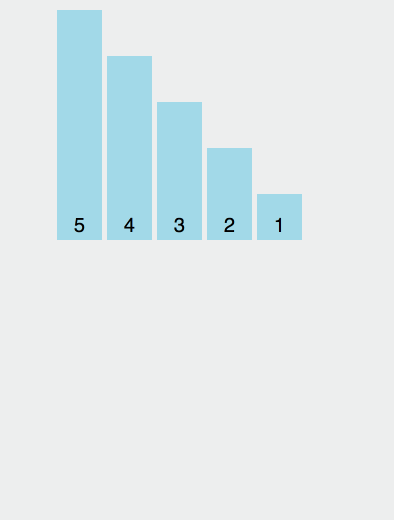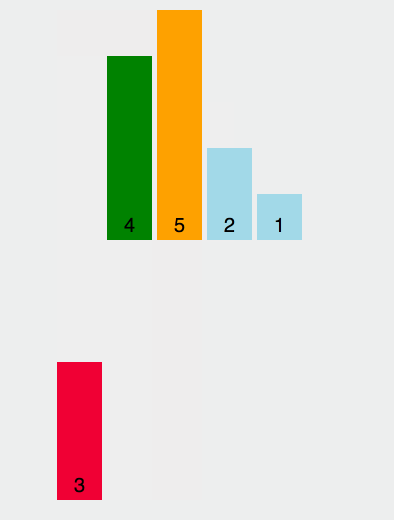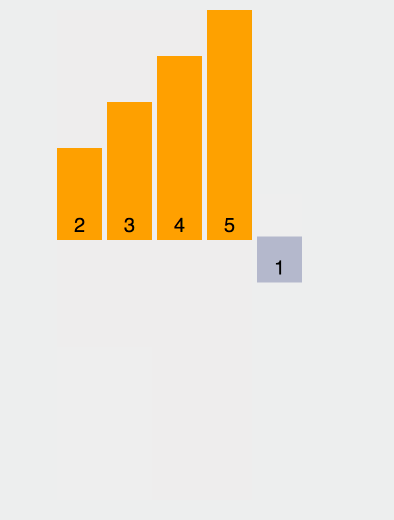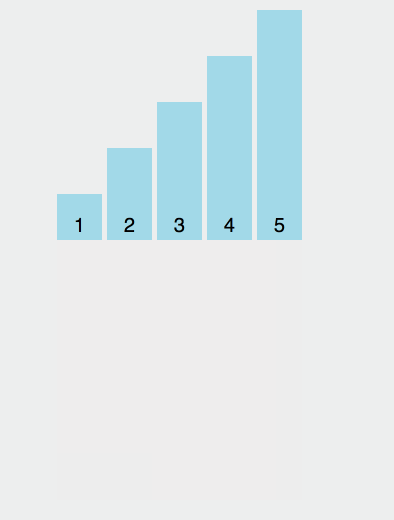
「ベースライン」として要素を選択します
「ベースライン」より小さい要素は「ベースライン」より大きい要素の左側に移動されます。 「ベースライン」は右の「ベースライン」「」に移動されます。
すべてのサブセットに 1 つの要素だけが残るまで、「ベースライン」の左右の 2 つのサブセットに対して、最初と 2 番目の手順を繰り返します。例:
var quickSort = function(arr) {
if (arr.length <= 1) { return arr; }
// 取数组的中间元素作为基准
var pivotIndex = Math.floor(arr.length / 2);
var pivot = arr.splice(pivotIndex, 1)[0];
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++){
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right));
};イメージ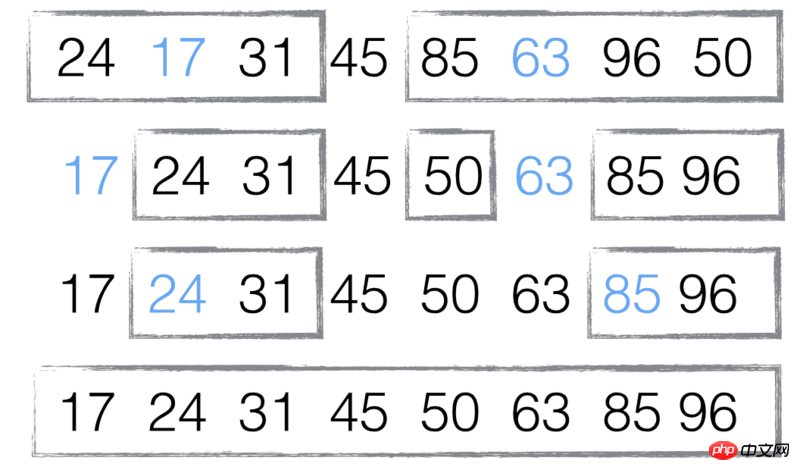
インプレースソートの実装図を見てみましょう:
緑色の要素がピボットのすぐ右側に配置され、紫色の要素が後ろに移動し、その後ピボットと最後の緑色の要素が入れ替わることがわかります。この時点で、ピボットが入っています。正しい位置、つまり前の要素はすべて基準値より小さい場合、後続のすべての要素は基準値より大きくなります。次に、前後の複数の要素を基準にして並べ替えます。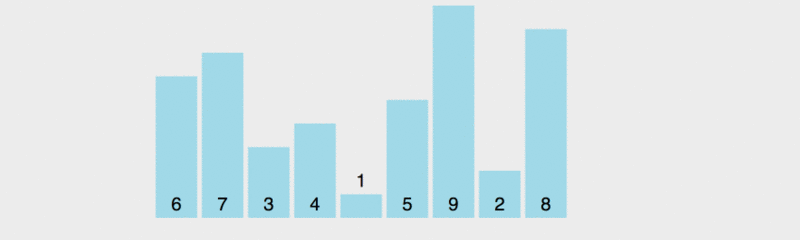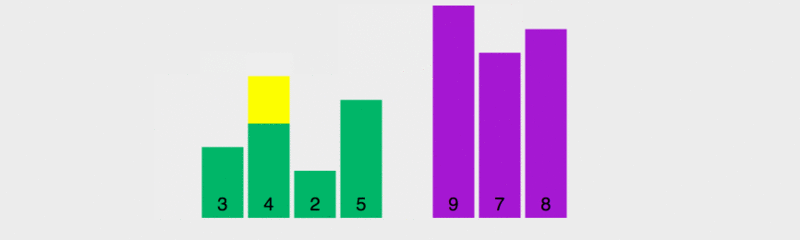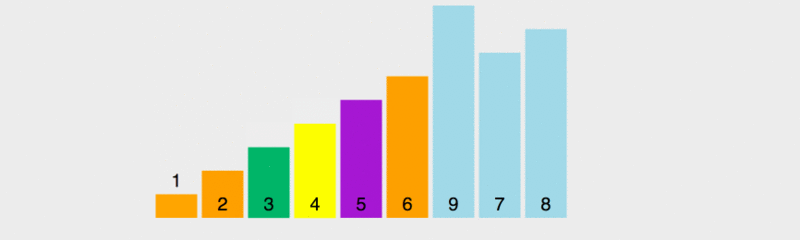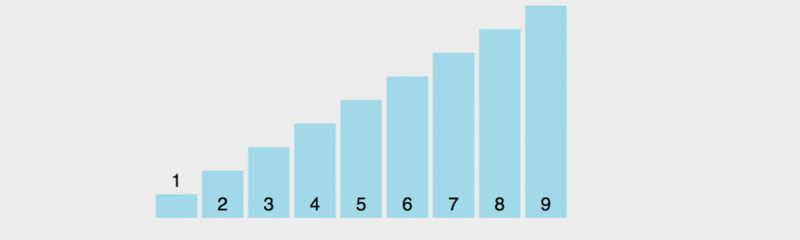 
インプレース実装
function quickSort(arr) {
// 交换元素
function swap(arr, a, b) {
var temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
function partition(arr, left, right) {
var pivot = arr[left];
var storeIndex = left;
for (var i = left + 1; i <= right; i++) {
if (arr[i] < pivot) {
swap(arr, ++storeIndex, i);
}
}
swap(arr, left, storeIndex);
return storeIndex;
}
function sort(arr, left, right) {
if (left < right) {
var storeIndex = partition(arr, left, right);
sort(arr, left, storeIndex - 1);
sort(arr, storeIndex + 1, right);
}
}
sort(arr, 0, arr.length - 1);
return arr;
}
console.log(quickSort(6, 7, 3, 4, 1, 5, 9, 2, 8))安定性
クイックソートは不安定なソートです。並べ替えが不安定であることを証明したい場合は、例を挙げるだけで十分です。
それでは、一つ育ててみましょう~
就以数组 [1, 2, 3, 3, 4, 5] 为例，因为基准的选择不确定，假如选定了第三个元素(也就是第一个 3) 为基准，所有小于 3 的元素在前面，大于等于 3 的在后面，排序的结果没有问题。可是如果选择了第四个元素(也就是第二个 3 )，小于 3 的在基准前面，大于等于 3 的在基准后面，第一个 3 就会被移动到 第二个 3 后面，所以快速排序是不稳定的排序。
阮一峰老师的实现中，基准取的是中间元素，而原地排序中基准取最左边的元素。快速排序的关键点就在于基准的选择，选取不同的基准时，会有不同性能表现。
快速排序的时间复杂度最好为 O(nlogn)，可是为什么是 nlogn 呢？来一个并不严谨的证明：
在最佳情况下，每一次都平分整个数组。假设数组有 n 个元素，其递归的深度就为 log2n + 1，时间复杂度为 O(n)[(log2n + 1)]，因为时间复杂度考察当输入值大小趋近无穷时的情况，所以会忽略低阶项，时间复杂度为：o(nlog2n)。
如果一个程序的运行时间是对数级的，则随着 n 的增大程序会渐渐慢下来。如果底数是 10，lg1000 等于 3，如果 n 为 1000000，lgn 等于 6，仅为之前的两倍。如果底数为 2，log21000 的值约为 10，log21000000 的值约为 19，约为之前的两倍。我们可以发现任意底数的一个对数函数其实都相差一个常数倍而已。所以我们认为 O(logn)已经可以表达所有底数的对数了，所以时间复杂度最后为： O(nlogn)。
而在最差情况下，如果对一个已经排序好的数组，每次选择基准元素时总是选择第一个元素或者最后一个元素，那么每次都会有一个子集是空的，递归的层数将达到 n，最后导致算法的时间复杂度退化为 O(n²)。
这也充分说明了一个基准的选择是多么的重要，而 v8 为了提高性能，就对基准的选择做了很多优化。
v8 选择基准的原理是从头和尾之外再选择一个元素，然后三个值排序取中间值。
当数组长度大于 10 但是小于 1000 的时候，取中间位置的元素，实现代码为：
// 基准的下标 // >> 1 相当于除以 2 (忽略余数) third_index = from + ((to - from) >> 1);
当数组长度大于 1000 的时候，每隔 200 ~ 215 个元素取一个值，然后将这些值进行排序，取中间值的下标，实现的代码为：
// 简单处理过
function GetThirdIndex(a, from, to) {
var t_array = new Array();
// & 位运算符
var increment = 200 + ((to - from) & 15);
var j = 0;
from += 1;
to -= 1;
for (var i = from; i < to; i += increment) {
t_array[j] = [i, a[i]];
j++;
}
// 对随机挑选的这些值进行排序
t_array.sort(function(a, b) {
return comparefn(a[1], b[1]);
});
// 取中间值的下标
var third_index = t_array[t_array.length >> 1][0];
return third_index;
}也许你会好奇 200 + ((to - from) & 15) 是什么意思？
& 表示是按位与，对整数操作数逐位执行布尔与操作。只有两个操作数中相对应的位都是 1，结果中的这一位才是 1。
以 15 & 127 为例：
15 二进制为： （0000 1111）
127 二进制为：（1111 1111）
按位与结果为：（0000 1111）＝ 15
所以 15 & 127 的结果为 15。
注意 15 的二进制为： 1111，这就意味着任何和 15 按位与的结果都会小于或者等于 15，这才实现了每隔 200 ~ 215 个元素取一个值。
终于到了看源码的时刻！源码地址为：https://github.com/v8/v8/blob/master/src/js/array.js#L758。
function InsertionSort(a, from, to) {
for (var i = from + 1; i < to; i++) {
var element = a[i];
for (var j = i - 1; j >= from; j--) {
var tmp = a[j];
var order = comparefn(tmp, element);
if (order > 0) {
a[j + 1] = tmp;
} else {
break;
}
}
a[j + 1] = element;
}
};
function QuickSort(a, from, to) {
var third_index = 0;
while (true) {
// Insertion sort is faster for short arrays.
if (to - from <= 10) {
InsertionSort(a, from, to);
return;
}
if (to - from > 1000) {
third_index = GetThirdIndex(a, from, to);
} else {
third_index = from + ((to - from) >> 1);
}
// Find a pivot as the median of first, last and middle element.
var v0 = a[from];
var v1 = a[to - 1];
var v2 = a[third_index];
var c01 = comparefn(v0, v1);
if (c01 > 0) {
// v1 < v0, so swap them.
var tmp = v0;
v0 = v1;
v1 = tmp;
} // v0 <= v1.
var c02 = comparefn(v0, v2);
if (c02 >= 0) {
// v2 <= v0 <= v1.
var tmp = v0;
v0 = v2;
v2 = v1;
v1 = tmp;
} else {
// v0 <= v1 && v0 < v2
var c12 = comparefn(v1, v2);
if (c12 > 0) {
// v0 <= v2 < v1
var tmp = v1;
v1 = v2;
v2 = tmp;
}
}
// v0 <= v1 <= v2
a[from] = v0;
a[to - 1] = v2;
var pivot = v1;
var low_end = from + 1; // Upper bound of elements lower than pivot.
var high_start = to - 1; // Lower bound of elements greater than pivot.
a[third_index] = a[low_end];
a[low_end] = pivot;
// From low_end to i are elements equal to pivot.
// From i to high_start are elements that haven&#39;t been compared yet.
partition: for (var i = low_end + 1; i < high_start; i++) {
var element = a[i];
var order = comparefn(element, pivot);
if (order < 0) {
a[i] = a[low_end];
a[low_end] = element;
low_end++;
} else if (order > 0) {
do {
high_start--;
if (high_start == i) break partition;
var top_elem = a[high_start];
order = comparefn(top_elem, pivot);
} while (order > 0);
a[i] = a[high_start];
a[high_start] = element;
if (order < 0) {
element = a[i];
a[i] = a[low_end];
a[low_end] = element;
low_end++;
}
}
}
if (to - high_start < low_end - from) {
QuickSort(a, high_start, to);
to = low_end;
} else {
QuickSort(a, from, low_end);
from = high_start;
}
}
}
var arr = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0];
function comparefn(a, b) {
return a - b
}
QuickSort(arr, 0, arr.length)
console.log(arr)我们以数组 [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0] 为例，分析执行的过程。
1.执行 QuickSort 函数 参数 from 值为 0，参数 to 的值 11。
2.10 < to - from < 1000 第三个基准元素的下标为 (0 + 11 >> 1) = 5，基准值 a[5] 为 5。
3.比较 a[0] a[10] a[5] 的值，然后根据比较结果修改数组，数组此时为 [0, 9, 8, 7, 6, 5, 4, 3, 2, 1, 10]
4.将基准值和数组的第(from + 1)个即数组的第二个元素互换，此时数组为 [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10]，此时在基准值 5 前面的元素肯定是小于 5 的，因为第三步已经做了一次比较。后面的元素是未排序的。
我们接下来要做的就是把后面的元素中小于 5 的全部移到 5 的前面。
5.然后我们进入 partition 循环，我们依然以这个数组为例，单独抽出来写个 demo 讲一讲
// 假设代码执行到这里，为了方便演示，我们直接设置 low_end 等变量的值
// 可以直接复制到浏览器中查看数组变换效果
var a = [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10]
var low_end = 1;
var high_start = 10;
var pivot = 5;
console.log(&#39;起始数组为&#39;, a)
partition: for (var i = low_end + 1; i < high_start; i++) {
var element = a[i];
console.log(&#39;循环当前的元素为：&#39;, a[i])
var order = element - pivot;
if (order < 0) {
a[i] = a[low_end];
a[low_end] = element;
low_end++;
console.log(a)
}
else if (order > 0) {
do {
high_start--;
if (high_start == i) break partition;
var top_elem = a[high_start];
order = top_elem - pivot;
} while (order > 0);
a[i] = a[high_start];
a[high_start] = element;
console.log(a)
if (order < 0) {
element = a[i];
a[i] = a[low_end];
a[low_end] = element;
low_end++;
}
console.log(a)
}
}
console.log(&#39;最后的结果为&#39;, a)
console.log(low_end)
console.log(high_start)6.此时数组为 [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10]，循环从第三个元素开始，a[i] 的值为 8，因为大于基准值 5，即 order > 0，开始执行 do while 循环，do while 循环的目的在于倒序查找元素，找到第一个小于基准值的元素，然后让这个元素跟 a[i] 的位置交换。
第一个小于基准值的元素为 1，然后 1 与 8 交换，数组变成 [0, 5, 1, 7, 6, 9, 4, 3, 2, 8, 10]。high_start 的值是为了记录倒序查找到哪里了。
7. このとき、a[i]の値は1となり、1と基底値5を交換すると、配列は[0, 1, 5, 7, 6, 9, 4, 3]となります。 、２、８、１０］の場合、low_endの値は１ずつ増加する。low_endの値は、基準値の位置を記録するためのものである。 [0, 1, 5, 7, 6, 9, 4, 3, 2, 8, 10]，low_end 的值加 1，low_end 的值是为了记录基准值的所在位置。
8.循环接着执行，遍历第四个元素 7，跟第 6、7 的步骤一致，数组先变成 [0, 1, 5, 2, 6, 9, 4, 3, 7, 8, 10]，再变成 [0, 1, 2, 5, 6, 9, 4, 3, 7, 8, 10]
9.遍历第五个元素 6，跟第 6、7 的步骤一致，数组先变成 [0, 1, 2, 5, 3, 9, 4, 6, 7, 8, 10]，再变成 [0, 1, 2, 3, 5, 9, 4, 6, 7, 8, 10]
10.遍历第六个元素 9，跟第 6、7 的步骤一致，数组先变成 [0, 1, 2, 3, 5, 4, 9, 6, 7, 8, 10]，再变成 [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10]
11.在下一次遍历中，因为 i == high_start，意味着正序和倒序的查找终于找到一起了，后面的元素肯定都是大于基准值的，此时退出循环
12.遍历后的结果为 [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10]，在基准值 5 前面的元素都小于 5，后面的元素都大于 5，然后我们分别对两个子集进行 QuickSort
13.此时 low_end 值为 5，high_start 值为 6，to 的值依然是 10，from 的值依然是 0，to - high_start < low_end - from 的结果为 true，我们对 QuickSort(a, 6, 10)，即对后面的元素进行排序，但是注意，在新的 QuickSort 中，因为 from - to 的值小于 10，所以这一次其实是采用了插入排序。所以准确的说，当数组长度大于 10 的时候，v8 采用了快速排序和插入排序的混合排序方法。
14.然后 to = low_end
[0, 1, 5, 2, 6, 9, 4, 3, 7] になります。 , 8, 10] になり、[0, 1, 2, 5, 6, 9, 4, 3, 7, 8, 10]9 になります。要素 6 は手順 6 および 7 と同じです。配列は最初に [0, 1, 2, 5, 3, 9, 4, 6, 7, 8, 10] になり、次に [0, 1, 2, 3, 5, 9, 4, 6, 7, 8, 10]10. ステップ 6 と 7 と同じように、6 番目の要素 9 を走査します。最初は [0, 1, 2, 3, 5, 4, 9, 6, 7, 8, 10] になり、次に [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10]11. 次の走査では、i == high_start であるため、前方検索と逆方向検索が最終的に一緒に見つかることを意味し、次の要素が必要です。ベンチマーク値より大きい場合、この時点でループを終了します12。走査後の結果は [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10] code> の場合、基本値 5 の前の要素はすべて 5 より小さく、後ろの要素はすべて 5 より大きい場合、2 つのサブセットに対してそれぞれ QuickSort を実行します13 このとき、low_end 値は 5 です。 、 high_start 値は 6 、 to の値は依然として 10 、 from の値は依然として 0 、 to - high_start < low_end - from の結果は true です。 > では、QuickSort(a, 6, 10) を使用します。つまり、次の場合、要素はソートされますが、新しい QuickSort では、from - to の値が 10 未満であるため、実際には挿入ソートが使用されることに注意してください。時間。つまり、 正確に言うと配列の長さが 10 を超える場合、v8 ではクイック ソートと挿入ソートのハイブリッド ソート方法が使用されます。 
14. 次に、to = low_end を 5 に設定します。while(true) であるため、to - from の値は 5 になり、InsertionSort(a) が実行されます。 、0、5)、つまり、参照値の前の要素に対して挿入ソートを実行します。
15. to - from
16.v8 配列に対してクイック ソートを実行した後、次に 2 つのサブセットに対してそれぞれ挿入ソートを実行し、最後に配列を正しくソートされた配列に変更します。
比較
最後に、挿入ソートとクイックソートを体験するための概略図を見てみましょう:
写真はhttps://www.toptal.com/developers/sorting-algorithmsからのものです🎜🎜特別シリーズ🎜🎜JavaScript 特別トピック シリーズのディレクトリ アドレス: https://github.com/mqyqingfeng/Blog。 🎜🎜JavaScript トピック シリーズは約 20 記事になる予定で、主に日常の開発におけるいくつかの機能ポイントの実装を研究します。たとえば、アンチシェイク、スロットル、重複排除、型判定、コピー、最大値、フラット化、カリー、再帰、特徴は、(xi) アンダースコアと jQuery の実装を研究することです。 🎜🎜🎜🎜🎜🎜🎜以上がJavaScript での v8 ソートソースコードに関する問題の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
